Тема 6. «Элементы комбинаторики»
ЗАДАЧИ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ПО МАТЕМАТИКЕ
СЕМЕСТР
Тема 6. «Элементы комбинаторики»
6.1. Вычислите: 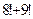
6.2. Вычислите: 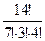
6.3. Вычислите: 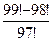
6.4. Вычислите: 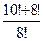
6.5. Вычислите: 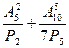
6.6. Вычислите: 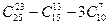
6.7. Сколькими способами можно составить расписание одного учебного дня из 6 различных
уроков?
6.8. Сколько различных пятизначных чисел можно составить из цифр 1, 2. 3, 4, 5 (цифры в одном
числе не должны повторяться)?
6.9. Сколькими способами из 10 игроков волейбольной команды можно выбрать стартовую
шестёрку?
6.10. 10 разных писем раскладывают по одному в 10 разных конвертов. Сколько существует
способов такого раскладывания?
6.11. В розыгрыше первенства по футболу принимают участие 16 команд, при этом любые две
команды играют между собой только один матч. Сколько всего календарных игр?
6.12. Сколько вариантов различных флагов из трёх горизонтальных полос разного цвета можно
составить, если есть полосы пяти разных цветов?
6.13. Сколькими разными способами можно назначить двух ребят на дежурство по столовой, если
в классе 25 учащихся?
6.14. Сколькими разными способами могут распределиться призовые места (первое, второе и
третье) между восемью хоккейными командами?
Тема 10. «Многогранники»
10.1. Найти площадь полной поверхности куба, ребро которого равно 3см.
10.2. Найти объём куба, ребро которого равно 2см.
10.3. В основании прямоугольного параллелепипеда лежит ромб, стороны которого 6см
и 8см. Высота параллелепипеда 10см. Найти площадь полной поверхности.
10.4. Длины рёбер прямоугольного параллелепипеда 6см, 8см и 12см. Найти длины его
диагоналей.
10.5. Высота прямой призмы 12см, а её основанием является прямоугольник, стороны
которого 6см и 8см. Найти площадь диагонального сечения призмы.
10.6. Высота правильной треугольной пирамиды равна 6см, а сторона основания 4см. Найти объём
пирамиды.
10.7. Найти полную поверхность правильной четырёхугольной пирамиды, высота
которой равна 2см, а сторона основания 4,2см.
10.8. В правильной четырёхугольной пирамиде высота равна 12см, апофема боковой
грани 13см. Найти боковое ребро.
10.9. Высота правильной четырёхугольной пирамиды 7см, а сторона основания 8см.
Найти боковое ребро пирамиды.
10.10.В правильной четырёхугольной пирамиде высота равна 8см, а боковое ребро
наклонено к плоскости основания под углом 45º. Найти объём пирамиды.
10.11.Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра
равны 13. Найдите площадь поверхности этой пирамиды.
10.12. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5
и 7, боковое ребро равно 4. Найдите объем призмы.
10.13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 3, а
высота равна 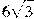 .
.
10.14. В правильной четырехугольной пирамиде высота равна 3, боковое ребро равно 10. Найдите
ее объем.
10.15. Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2 и 7.
Найдите его площадь поверхности.
10.16. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5
и 12, высота призмы равна 8. Найдите площадь ее поверхности.
10.17. Найдите площадь поверхности правильной четырехугольной
пирамиды, стороны основания которой равны 48 и высота равна 7.
10.18. Найдите площадь боковой поверхности правильной четырехугольной пирамиды,
сторона основания которой равна 24 и высота равна 16.
10.19. Найдите объем пирамиды, высота которой равна 3, а основание — прямоугольник со
сторонами 5 и 3.
Тема 11. «Тела вращения»
11.1. Найти объём цилиндра, высота которого 5см, а радиус основания 3см.
11.2. Радиус основания цилиндра 6см, а его образующая 10см. Найти площадь осевого
сечения цилиндра.
11.3. Осевым сечением цилиндра является квадрат, диагональ которого 4см. Найти площадь
полной поверхности цилиндра.
11.4. Прямоугольник, стороны которого 4см и 6см, вращается вокруг большей стороны.
Найти площадь поверхности тела вращения.
11.5. Найти объём конуса, образующая которого 5см, а радиус основания 3см.
11.6. Найти высоту конуса, образующая которого равна 10см, а радиус основания 8см.
11.7. Угол при основании осевого сечения конуса равен 60º, радиус конуса 3см. Найти площадь
боковой поверхности конуса.
11.8. Высота и радиус основания конуса соответственно равны 3см и 4см. Найти
боковую поверхность конуса.
11.9. Образующая конуса наклонена к плоскости основания под углом 45º, а его высота
равна 12см. Найти площадь боковой поверхности конуса.
11.10. Плоскость α касается шара в точке А. Точка С принадлежит плоскости α. Найти площадь
поверхности шара, если АС = 12см, ОС = 13см. ( О – центр шара).
11.11. Найти площадь сечения шара радиуса 5см плоскостью, проведённой на расстоянии
4см от центра.
11.12. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности
цилиндра.
11.13. Найдите объем V конуса, образующая которого равна 3 и наклонена к плоскости основания
под углом 30 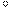 .
.
11.14. Высота конуса равна 3, образующая равна 6. Найдите его объем
11.15. Конус получается при вращении равнобедренного прямоугольного треугольника
ABC вокруг катета, равного 15. Найдите его объем.
11.16. Высота конуса равна 20, образующая равна 25. Найдите площадь его полной поверхности.
11.17. Радиус основания конуса равен 28, высота равна 21. Найдите площадь полной поверхности
конуса.
ЗАДАЧИ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ПО МАТЕМАТИКЕ
СЕМЕСТР
Тема 6. «Элементы комбинаторики»
6.1. Вычислите: 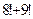
6.2. Вычислите: 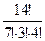
6.3. Вычислите: 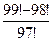
6.4. Вычислите: 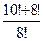
6.5. Вычислите: 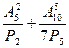
6.6. Вычислите: 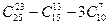
6.7. Сколькими способами можно составить расписание одного учебного дня из 6 различных
уроков?
6.8. Сколько различных пятизначных чисел можно составить из цифр 1, 2. 3, 4, 5 (цифры в одном
числе не должны повторяться)?
6.9. Сколькими способами из 10 игроков волейбольной команды можно выбрать стартовую
шестёрку?
6.10. 10 разных писем раскладывают по одному в 10 разных конвертов. Сколько существует
способов такого раскладывания?
6.11. В розыгрыше первенства по футболу принимают участие 16 команд, при этом любые две
команды играют между собой только один матч. Сколько всего календарных игр?
6.12. Сколько вариантов различных флагов из трёх горизонтальных полос разного цвета можно
составить, если есть полосы пяти разных цветов?
6.13. Сколькими разными способами можно назначить двух ребят на дежурство по столовой, если
в классе 25 учащихся?
6.14. Сколькими разными способами могут распределиться призовые места (первое, второе и
третье) между восемью хоккейными командами?
