Аналитическое выравнивание по показательной функции.

Показательная функция аналитического выравнивания имеет вид:

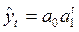(6.45)

Для определения параметров уравнения также используют МНК, для чего предварительно логарифмируют уровни, и тогда логарифмы уровней отражаются линейной функцией:

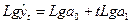(6.46)

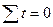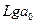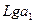Примем , тогда параметры уравнений и рассчитывают как:

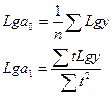(6.47)

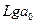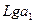Рассчитав и определим 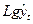, затем, потенцируя 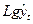находим .

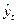Далее проводят оценку надежности полученного уравнения с помощью критерия Фишера (см. выше).

1.6.2.4 Анализ сезонных колебаний ряда динамик

При анализе динамических рядов может быть обнаружена периодичность колебаний уровней динамического ряда, то есть наблюдается устойчивое отклонение уровней от тенденции в зависимости от периода времени (внутригодичного, внутриквартального, внутримесячного и т.д.). в данном случае статистика говорит, что в динамическом ряду наблюдаются сезонные колебания.

Сезонные колебания – внутригодичные (внутриквартальные, внутримесячные и т.д.) изменения в ряду динамики, вызванные специфическими условиями, возникающими в определенном периоде года (квартала, месяца, и т.д.). Например, в сезонность наблюдается по уровню удоев, яйценоскости, потребление топлива, сезонность наблюдается в потреблении определенных товаров и т.д.

Изучения явления сезонности имеет большое практическое значения для минимизации отрицательного воздействия сезонности на уровень развития производства, торговли и т.д. Наиболее часто, сезонные колебания статистика изучает при помощи следующих методов:

1. метод абсолютных разностей и относительных разностей

2. расчет индексов сезонности

Метод абсолютных и относительных разностей.

При методе абсолютных разностей используют непосредственно размеры данных разностей. При методе относительных разностей определяют отношения абсолютных размеров указанных разностей к среднему уровню. При расчете абсолютных и относительных разностей:

1. определяют абсолютные уровни ряда

2. рассчитывают средний месячный уровень ряда

3. сопоставляя абсолютные уровни ряда (находя разности или отношения) определяют показатели сезонности (абсолютные или относительные).

Расчет индексов сезонности.

Индекс сезонности показывает, во сколько раз фактический уровень динамического ряда 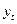на определенный момент времени 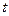больше среднего уровня 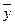либо выровненного, методом скользящей средней, либо методом аналитического выравнивания, уровня. При анализе сезонных колебаний динамического ряда рассматривают развития по месяцам (кварталам, неделям, и т.д.) одного или нескольких лет (кварталов, месяцев и т.д.). Метод определения индекса сезонности зависит от того, наблюдается наличие тренда в изучаемом ряду или тренд отсутствует.

Если тренд отсутствует, то

· для каждого конкретного месяца (квартала, недели и т.д.):

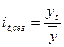(6.48)

где 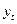- уровень динамического ряда за месяц (квартал, неделю и т.д.)

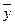- средний уровень за весь период (год, квартал и т.д.)

· для больших (средних) промежутков времени (за несколько месяцев, кварталов и т.д.)

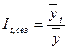или 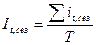(6.49)

где 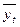- средний уровень динамического ряда за одноименные месяцы (кварталы, недели и т.д.)

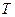- число лет.

2. Если в динамическом ряду существует ярко выраженный тренд, расчет проводится следующим образом

а) для каждого уровня определяют значения выровненного уровня

b) рассчитывают, как отношение фактического уровня динамического ряда к выровненному уровню по тренду либо как отношение средней из фактических уровней одноименных месяцев (кварталов, недель и т.д.) к средней из выровненных данных по тем же месяцам (кварталам, неделям и т.д.).

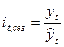либо 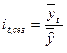(6.50)

c) также находят среднее из отношений фактических уровней к выровненному уровню для одноименных месяцев (кварталов, недель и т.д.)

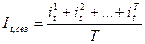(6.51)

где 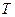- число лет

1.6.2.5 Экстраполяция и интерполяция

Исследование динамических рядов социально-экономических явлений, определения закономерности их развития во времени создают основу для статистического прогнозирования (экстраполяции) и интерполяции изучаемого явления.

Экстраполяция в динамике предполагает распространение полученных выводов, полученных в прошлом на будущее время. При этом предполагается, что закономерность развития, динамического ряда сохраняется в будущем.

Самый простой метод экстраполяции это применение средних характеристик ряда динамики: среднего абсолютного прироста и среднего темпа роста.

Более часто применяют экстраполяцию динамического ряда по аналитически выровненным рядам.

После того как по фактическому динамическому ряду выявлен тренд (выровненный ряд, отражающий тенденцию развития) экстраполяцию можно провести двумя методами:

1. графический метод. Заключается в построении точного графика выровненного динамического ряда, на котором линию полученного тренда продлевают до интересующей нас даты.

2. аналитический метод. При данном методе в рассчитанное аналитическое уравнение подставляют номер интересующего нас периода.

Выявление основной тенденции развития дает возможность определять также значение недостающего члена ряда – интерполяция. Также проводится графическим и аналитическим методом.