Задача об обнаружении эффекта обработки в предположении о совместном нормальном распределении. Критерий Стьюдента для проверки соответствующей гипотезы. Проведение теста в пакете R.

Теория:

Пусть есть 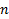объектов, над которыми 2 раза проводились измерения (до и после некоторой дополнительной обработки объектов):

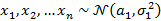
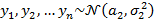
Мы хотим проверить гипотезу о том, что никакого эффекта от обработки объекта не было.

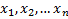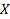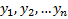Пусть измерения являются порождениями случайной величины , а порождениями случайной величины 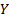. Тогда совместное распределение этих случайных величин имеет вид:

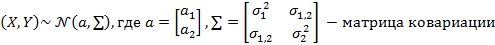
В качестве нулевой гипотезы будем рассматривать:

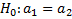
Рассмотрим разность случайных величин 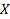и 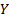в качестве новой случайной величины:

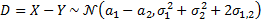
Теперь нулевую гипотезу можно переписать в виде:

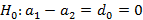
В качестве альтернативной возьмём гипотезу:

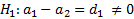
Это задача о проверке простой параметрической гипотезы против простой альтернативы. Для нормального распределения в билетах 17-18 показано, что наиболее мощный критерий для проверки такой гипотезы основан на следующей статистике:

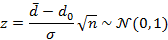
Однако, 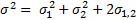мы не знаем, поэтому нам придётся вместо дисперсии использовать её оценку (несмещённую) по выборке. Таким образом мы перейдём к следующей статистике:

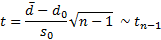
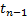– t-распределение (распределение Стьюдента) с 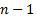степенью свободы. Критерий Стьюдента (t-критерий) заключается в вычислении t-статистики и подсчёте p-value, показывающего, насколько типичное для t-распределения значение получилось. При маленьком p-value ( 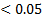например) мы отвергаем .

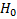В языке R вся вышеописанная процедура проделывается одной командой:

t.test(x, y, paired = TRUE)

Практика в R:

Пример.На группе из 10 человек тестировали лекарство от бессоницы. Сначала им давали плацебо, а потом настоящее лекарство. Результаты исследования сохранены в кадре данных sleep. Первая колонка (extra) – изменение длительности сна в часах. Вторая колонка (group) – номер группы (1 – плацебо, 2 – лекарство). Третья колонка (id) – номер испытуемого в группе.

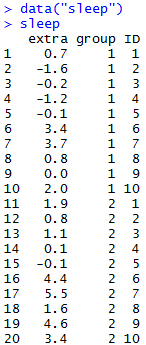
Проверим для начала, имеет ли разность переменных extra между двумя группами нормальное распределение (иначе критерий Стьюдента применять нельзя):

with(sleep, qqnorm(subset(extra, group == '1') - subset(extra, group == '2')))

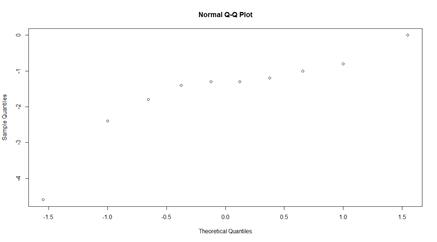
Точки на вероятностной бумаге выстроены примерно вдоль прямой, поэтому считаем разность нормально распределённой. Теперь применим критерий Стьюдента (односторонний, так как нам надо убедиться, что лекарство помогает увеличить продолжительность сна, а не наоборот):

t.test(extra ~ group, sleep, paired = TRUE, alternative = "less")

Paired t-test

data: extra by group

t = -4.0621, df = 9, p-value = 0.001416

alternative hypothesis: true difference in means is less than 0

95 percent confidence interval:

-Inf -0.8669947

sample estimates:

mean of the differences

-1.58

t – значение t-статистики. df – число степеней свободы t-распределения (вроде какое надо, т.к. n-1 = 9). p-value < 0.01, поэтому мы можем смело отвергать гипотезу о том, что от лекарства нет положительного эффекта, т.е. скорее всего лекарство действительно помогает при бессонице.