Метод получения выборки значений случайной величины с помощью генератора псевдослучайных чисел. Метод обратной функции, метод отсечения.
Теория:
Датчики случайных чисел:
Физические (ГСЧ): температура процессора, кол-во тактов работы системы, радиосигналы из космоса и т.д. Есть ассемблерная команда для генерации. В языке R прямой возможности для генерации таких чисел нет.
Генераторы псвевдослучайных чисел (ГПСЧ): детерминированные числовые последовательности, в силу своей сложности кажущиеся случайными. Примеры: датчик Фибоначчи (примитивный: можно относительно легко угадать следующее число), вихрь Мерсенна (крутой: очень большой период, низкая корреляция, может равномерно заполнять 608-мерный куб).
Обычно, ГПСЧ или ГСЧ дают число, равномерно распределённое на отрезке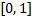 
. Хотелось бы получать числа из любого наперёд заданного распределения. Для непрерывных с.в. есть как минимум 2 способа генерации случайных чисел из такого распределения на основе чисел из другого (известного) распределения:
Метод обратной функции
Пусть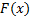 
– функция распределения, число из которого мы хотим получить, 
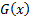– обратная функция к 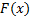(она существует на интервале 
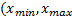) строгой монотонности ), 
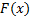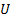– случайная величина, распределённая равномерно в 
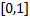. Заметим, что:
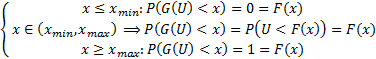
То есть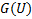 
– случайная величина, распределённая по нужному нам закону распределения.
Метод отсечения
Пусть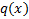 
– плотность нужного нам распределения, а 
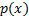– плотность какого-то популярного распределения, причём 
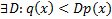. Тогда алгоритм генерации такой:
Генерируем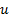 
из равномерного на 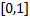распределения и 
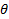из распределения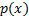
Если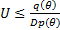 
, то возвращаемся на шаг 1. Иначе, 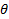– искомое число из распределения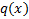
Практика:
В языке R есть функции для генерации чисел из большинства популярных распределений, например (в дальнейшем,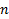 
– число генерируемых чисел):
runif(n, min = 0, max = 1)
Равномерное непрерывное распределение
rnorm(n, mean = 0, sd = 1)
Нормальное распределение
rpois(n, lambda)
Распределение Пуассона
?distributions
Чтобы посмотреть все остальные в справке
Однако, часто возникает необходимость в генерации чисел из какого-нибудь специфического распределения, для которого в языке R функция не предусмотрена.
Метод обратной функции:
1) На бумажке (или в каком-нибудь вольфраме символьно) считаем функцию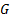 
. Для этого надо выразить 
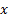через 
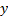из уравнения 
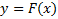для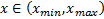 
2) Печатаем полученную функцию в скрипте языка R:
G <- function(y)
{
…
}
3) В консоли или отдельном скрипте пишем такую штуку и получаем выборку нашего распределения из 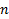значений:
x <- apply(runif(n), G)
Генерируем рандомный seed с помощью вихря Мерсена
RNGkind("Mersenne-Twister")
.Random.seed[1:6]
[1] 403 624 1744731888 -1305618895 -658111938 -1494552153
.Random.seed[1:6]
[1] 403 624 -682825554 957688151 -228424276 -1621440835
Вычисление интегралов методом Монте–Карло в пакете R. Неоднозначность в разложении подынтегральной функции и ее влияние на эффективность метода.
Теория:
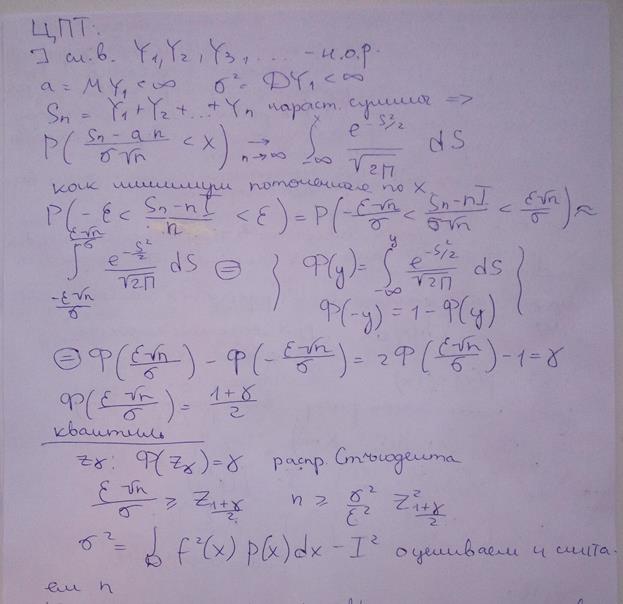
Практика в R:
#Считаем интеграл x^3 как среднее выборочное, где p(x) = 1, f(x) = x^3
fu <- function() {
mean(runif(1000)^3)
}
replicate(10,fu())
[1] 0.2558692 0.2460371 0.2469030 0.2484455 0.2374155 0.2406529 0.2424714 0.2538970
[9] 0.2479572 0.2526416