Выборка, выборочное распределение одномерной случайной величины. Построение эмпирической плотности и эмпирической функции распределения в пакете R.

Выборка, выборочное распределение одномерной случайной величины. Построение эмпирической плотности и эмпирической функции распределения в пакете R.

Теория:

Эмпирическую плотность можно оценить с помощью гистограммы, ядерных оценок.
K(x) – четная, интегрируемая:

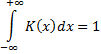
Пусть h > 0, тогда:

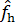(x) =

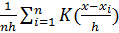
где 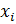, i = 1:n – значения выборки

Рассмотрим некоторые ядра:

Практика в R:

density(x, bw = "nrd0", adjust = 1,

kernel = c("gaussian", "epanechnikov", "rectangular",

"triangular", "biweight",

"cosine", "optcosine"),

weights = NULL, window = kernel, width,

give.Rkern = FALSE,

n = 512, from, to, cut = 3, na.rm = FALSE, ...)

Обязательные параметры: выборка, ядро, используя параметр kernel. Так же можно указать критерий по параметру сглаживания или его численное значение - параметр bw = "nrd0", (другие. так же указывать как строковую константу. nrd, ucv, bcv, SJ).

ecdf(x)

На вход только выборку.

Также добавив приставку d – плотность или p – функция распределения, можно получить соответственно плотность или функцию распределения указанного после приставки закона распределения:

pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
dunif(x, min = 0, max = 1, log = FALSE)

Выборочные числовые характеристики случайных величин. Оценка основных выборочных числовых характеристик в пакете R.

Теория:

Практика в R:

func.mean <- function() {

#Выборочное среднее для вектора

mean(trees$Girth)

[1] 13.24839

#Выборочное среднее для кадра данных

mean(trees)

#При отсутствующих значениях (na.rm=FALSE - NA, na.rm=TRUE - пропустит NA)

mean(c(1,2,NA))

[1] NA

mean(c(1,2,NA),na.rm=TRUE)

[1] 1.5

}

func.mediana <- function() {

#Выборочная медиана

median(trees$Girth)

}

func.quantile <- function() {

#Квантиль уровней 0, 25, 50, 75, 100 процентов - вероятность того, что нет значений выше

quantile(trees$Girth)

0% 25% 50% 75% 100%

8.30 11.05 12.90 15.25 20.60

#Квантиль уровней seq(0,1,0.1)

quantile(trees$Girth, seq(0,1,0.1))

0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%

8.3 10.5 11.0 11.2 11.4 12.9 13.7 14.2 16.3 17.9 20.6

}

func.var <- function() {

#Вычисление несмещенной выборочной дисперсии (тупо делится на n-1, а не на n) для кадра данных

var(trees)

#Для вектора

var(trees$Girth)

}

func.sqrt_disp <- function() {

#Вычисление среднеквадратичного отклонения

sd(trees$Girth)

}

func.diff <- function() {

#Находим min и max значения с помощью range и находим размах, используя diff

min_max = range(trees$Girth)

diff(min_max)

}

func.IQR <- function() {

#Выборочный междукваРтильный размах (между 1/4 и 3/4 кваНтилями)

IQR(trees$Girth)

}

Типы статистических данных. Частотные распределения. Маргинальные частотные распределения. Проблема нахождения выборочных числовых характеристик по группированным данным. Ее решение в пакете R.

Теория:

Практика в R:

Таблица частот cтроится функцией:

table(x,…)

На вход выборка или несколько выборок если хотим найти многомерное частотное распределение.

cut(x,br)

На входе выборка и массив из точек, которыми вся область значений выборки разбивается на интервалы. Функция возвращает не список x1,…,xN – т.е. выборку, а список интервалов, которым принадлежат x1,…,xN соответственно

x <- c(0,1,2,3,4,5,1,2,3,4,12,12,31,23,12,14,13,1,1,1,2,3)

range(x)

[1] 0 31

br <- seq(-1,31,4)

x.cut <- cut(x,br)

x.cut

[1] (-1,3] (-1,3] (-1,3] (-1,3] (3,7] (3,7] (-1,3] (-1,3] (-1,3] (3,7]

[11] (11,15] (11,15] (27,31] (19,23] (11,15] (11,15] (11,15] (-1,3] (-1,3] (-1,3]

[21] (-1,3] (-1,3]

Levels: (-1,3] (3,7] (7,11] (11,15] (15,19] (19,23] (23,27] (27,31]
table(x.cut)

(-1,3] (3,7] (7,11] (11,15] (15,19] (19,23] (23,27] (27,31]

12 3 0 5 0 1 0 1

y<-c('a','v','a','s','s')

table(y)

y

A s v

2 2 1

Маргинальные частоты – для многомерных частотных распределений можно посчитать частоту по какому-то одному признаку или по нескольким. Пример:

attach(iris)

i.l <-cut(Sepal.Length,breaks=6)

i.w <-cut(Sepal.Width,breaks=6)

table(i.l,i.w)

I.w

i.l (2,2.4] (2.4,2.8] (2.8,3.2] (3.2,3.6] (3.6,4] (4,4.4]

(4.3,4.9] 2 1 14 5 0 0

(4.9,5.5] 5 4 3 15 8 2

(5.5,6.1] 2 17 13 1 2 1

(6.1,6.7] 2 10 17 6 0 0

(6.7,7.3] 0 1 11 1 0 0

(7.3,7.9] 0 3 2 0 2 0

table.i <-table(i.l,i.w)

margin.table(table.i,1)

I.l

(4.3,4.9] (4.9,5.5] (5.5,6.1] (6.1,6.7] (6.7,7.3] (7.3,7.9]

22 37 36 35 13 7

margin.table(table.i,2)

I.w

(2,2.4] (2.4,2.8] (2.8,3.2] (3.2,3.6] (3.6,4] (4,4.4]

11 36 60 28 12 3

Сначала построили таблицу частот по двум параметрам, потом посчитали маргинальные частоты по первому и второму признакам. По первому – просуммировали строки, по второму столбцы

Далее для трех признаков, и маргинальные частоты по 2-м из них

table(Species,i.l,i.w)->tb.i.sp

ftable(tb.i.sp)

i.w (2,2.4] (2.4,2.8] (2.8,3.2] (3.2,3.6] (3.6,4] (4,4.4]

Species i.l

setosa (4.3,4.9] 1 0 14 5 0 0

(4.9,5.5] 0 0 2 15 8 2

(5.5,6.1] 0 0 0 0 2 1

(6.1,6.7] 0 0 0 0 0 0

(6.7,7.3] 0 0 0 0 0 0

(7.3,7.9] 0 0 0 0 0 0

versicolor (4.3,4.9] 1 0 0 0 0 0

(4.9,5.5] 5 4 1 0 0 0

(5.5,6.1] 1 11 10 1 0 0

(6.1,6.7] 2 2 8 1 0 0

(6.7,7.3] 0 1 2 0 0 0

(7.3,7.9] 0 0 0 0 0 0

virginica (4.3,4.9] 0 1 0 0 0 0

(4.9,5.5] 0 0 0 0 0 0

(5.5,6.1] 1 6 3 0 0 0

(6.1,6.7] 0 8 9 5 0 0

(6.7,7.3] 0 0 9 1 0 0

(7.3,7.9] 0 3 2 0 2 0

margin.table(tb.i.sp,c(1,3))

I.w

Species (2,2.4] (2.4,2.8] (2.8,3.2] (3.2,3.6] (3.6,4] (4,4.4]

Setosa 1 0 16 20 10 3

Versicolor 9 18 21 2 0 0

Virginica 1 18 23 6 2 0

Проблема нахождения выборочных числовых характеристик по группированным данным.

То есть у нас вместо выборки таблица частот. Для поиска числовых характеристик требуются другие формулы они просты, но получается нужно переписывать все функции R для работы с выборками под группированные данные. Вместо этого создатели языка предложили следующее решение: по группированным данным, генерировать фиктивную выборку.

a<-rbinom(10,10,0.2)

mean(a)

[1] 1.7

table(a)

a

0 1 2 3

1 3 4 2

rep(c(0,1,2,3),c(1,3,4,2))->a.fake

mean(a.fake)

[1] 1.7

a.fake

[1] 0 1 1 1 2 2 2 2 3 3

a

[1] 1 1 3 0 2 2 2 2 3 1

Метод обратной функции

Пусть 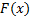– функция распределения, число из которого мы хотим получить, 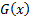– обратная функция к 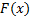(она существует на интервале 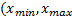) строгой монотонности 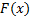), 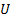– случайная величина, распределённая равномерно в 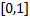. Заметим, что:

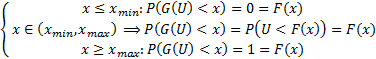
То есть 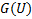– случайная величина, распределённая по нужному нам закону распределения.

Метод отсечения

Пусть 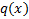– плотность нужного нам распределения, а 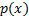– плотность какого-то популярного распределения, причём 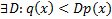. Тогда алгоритм генерации такой:

Генерируем 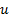из равномерного на 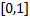распределения и 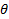из распределения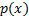

Если 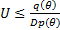, то возвращаемся на шаг 1. Иначе, 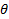– искомое число из распределения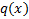

Практика:

В языке R есть функции для генерации чисел из большинства популярных распределений, например (в дальнейшем, 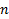– число генерируемых чисел):

runif(n, min = 0, max = 1)

Равномерное непрерывное распределение

rnorm(n, mean = 0, sd = 1)

Нормальное распределение

rpois(n, lambda)

Распределение Пуассона

?distributions

Чтобы посмотреть все остальные в справке

Однако, часто возникает необходимость в генерации чисел из какого-нибудь специфического распределения, для которого в языке R функция не предусмотрена.

Метод обратной функции:

1) На бумажке (или в каком-нибудь вольфраме символьно) считаем функцию 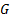. Для этого надо выразить 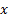через 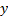из уравнени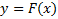я для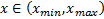

2) Печатаем полученную функцию в скрипте языка R:

G <- function(y)

{

…

}

3) В консоли или отдельном скрипте пишем такую штуку и получаем выборку нашего распределения из 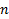значений:

x <- apply(runif(n), G)

Lambda1 lambda2

2.149147 3.528324

Постановка задачи

Пусть случайная величина Х имеет функцию распределения .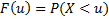

Односторонние интервалы: ­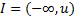– левый; ­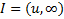– правый.

Двусторонний интервал: .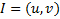

Доверительная вероятность: .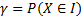

Задача: по заданной доверительной вероятности 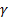требуется вычислить .

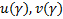Решение этой задачи находится через квантили распределения.

Квантиль распределения:

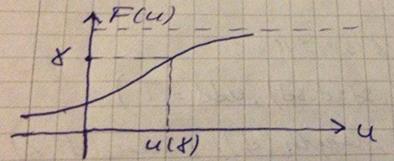
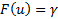– неявное уравнение. Требуется найти 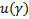– квантиль уровня .

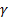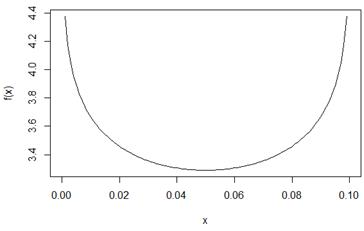
Пример

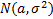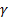, -фикс.

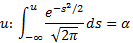
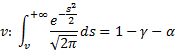
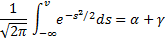
gm <- 0.9

f <- function(a) {

qnorm(gm + a, 0, 1) – qnorm(a, 0, 1)

}

curve(f, 0, 1 - gm)

Пусть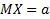

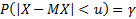
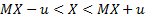
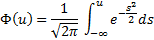
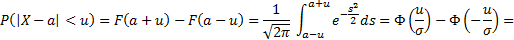
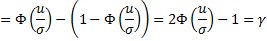
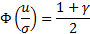
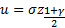
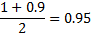
2*qnorm(0.95,0,1) # = 3.289707 – минимум функции на графике выше

Гипотезы

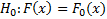– нулевая гипотеза

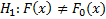– альтернативная гипотеза

Простая гипотеза – гипотеза, которой удовлетворяет только одно распределение вероятности

Сложная гипотеза – несколько распределений

Data: x.t

X-squared = 6.913, df = 10, p-value = 0.7336

chisq.test(x.t, p=pr.wrong) #отвергаем

Data: x.t

X-squared = 55.28, df = 8, p-value = 3.895e-09

15. Методы проверки нормальности данных при неизвестных параметрах распределения (вероятностная бумага, критерии Лильи – Фора).

Теория:

Практика в R:

library("nortest")

lillie.test(iris$Sepal.Width)

Z test for the mean value

data:

= -0.59725, p-value = 0.7248

Decision Accepted

Power 0.9996034

Welch Two Sample t-test

data: log(myx$MYXA30) and log(myx$MYXA60)

t = -0.37751, df = 29.213, p-value = 0.7085

Mean of x mean of y

2.807217 2.960523

Data: x by grp

Kruskal-Wallis chi-squared = 1.712, df = 2, p-value = 0.4249

Pearson's Chi-squared test

Data: tab

X-squared = 568.57, df = 12, p-value < 2.2e-16

Rho

0.9547151

Data: tab

p-value = 0.009423

0.001034782 0.656954980

sample estimates:

Odds ratio

0.05851868

Модель Гаусса-Маркова

,

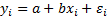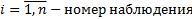
(1 вход и 1 выход)

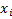– неслучайная величина

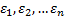– н.о.р.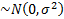

Неизвестные параметры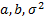

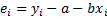– наблюдаемые погрешности

0.7143

plot(alcohol$x, alcohol$y)

abline(alcohol.lm, col="blue")

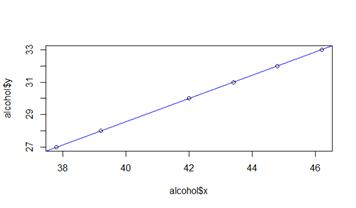
summary(alcohol.lm)

Call:

lm(formula = y ~ x - 1, data = alcohol)

Residuals:

1 2 3 4 5 6

E-14 -6.228e-16 2.552e-15 -4.459e-15 -4.270e-15 -4.081e-15

Coefficients:

Estimate Std. Error t value Pr(>|t|)

x 7.143e-01 5.524e-17 1.293e+16 <2e-16 ***

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

587.320391 -3.942494 0.008115

plot (gal$h, gal$d)

lines (gal$h, gal.lm$fitted.values)

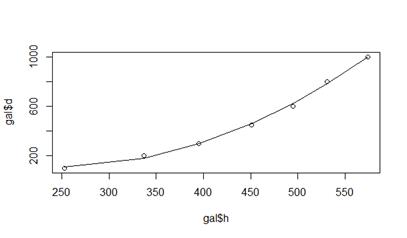
summary(gal.lm)

Call:

lm(formula = d ~ h + I(h^2), data = gal)

Residuals:

1 2 3 4 5 6 7

-9.311 19.672 3.800 -9.883 -24.198 17.992 1.928

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 5.873e+02 1.220e+02 4.813 0.008564 **

h -3.942e+00 6.134e-01 -6.428 0.003012 **

I(h^2) 8.115e-03 7.351e-04 11.040 0.000383 ***

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Shapiro-Wilk normality test

data: gal.lm$residuals

W = 0.94492, p-value = 0.6834

(gal.lm3 = update(gal.lm, . ~ . + I(h ^ 3)))

Call:

lm(formula = d ~ h + I(h^2) + I(h^3), data = gal)

Coefficients:

(Intercept) h I(h^2) I(h^3)

-6.902e+01 1.260e+00 -4.983e-03 1.056e-05

plot (gal$h, gal$d)

lines (gal$h, gal.lm3$fitted.values)

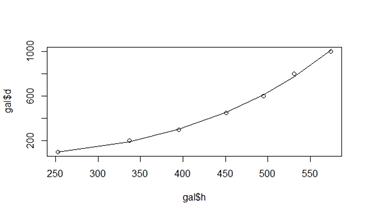
summary(gal.lm3)

Call:

lm(formula = d ~ h + I(h^2) + I(h^3), data = gal)

Residuals:

1 2 3 4 5 6 7

-1.808 6.237 -1.846 -4.108 -14.097 24.453 -8.832

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) -6.902e+01 5.020e+02 -0.137 0.899

h 1.260e+00 3.921e+00 0.321 0.769

I(h^2) -4.983e-03 9.792e-03 -0.509 0.646

I(h^3) 1.055e-05 7.872e-06 1.341 0.272

Shapiro-Wilk normality test

data: gal.lm3$residuals

W = 0.89196, p-value = 0.285

(gal.lm4 = update(gal.lm3, . ~ . - I(h ^ 3)))

Call:

lm(formula = d ~ h + I(h^2), data = gal)

Coefficients:

(Intercept) h I(h^2)

587.320391 -3.942494 0.008115

summary(gal.lm4)

Call:

lm(formula = d ~ h + I(h^2), data = gal)

Residuals:

1 2 3 4 5 6 7

-9.311 19.672 3.800 -9.883 -24.198 17.992 1.928

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 5.873e+02 1.220e+02 4.813 0.008564 **

h -3.942e+00 6.134e-01 -6.428 0.003012 **

I(h^2) 8.115e-03 7.351e-04 11.040 0.000383 ***

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Min 1Q Median 3Q Max

-4.6195 -1.1002 -0.1656 1.7451 4.1976

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) -2.977e-01 9.636e-01 -0.309 0.76

I(Height * Girth^2) 2.124e-03 5.949e-05 35.711 <2e-16 ***

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

1 2

24.997246 1.576019

Выборка, выборочное распределение одномерной случайной величины. Построение эмпирической плотности и эмпирической функции распределения в пакете R.

Теория:

Эмпирическую плотность можно оценить с помощью гистограммы, ядерных оценок.
K(x) – четная, интегрируемая:

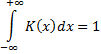
Пусть h > 0, тогда:

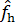(x) =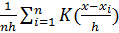

где 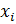, i = 1:n – значения выборки

Рассмотрим некоторые ядра:

Практика в R:

density(x, bw = "nrd0", adjust = 1,

kernel = c("gaussian", "epanechnikov", "rectangular",

"triangular", "biweight",

"cosine", "optcosine"),

weights = NULL, window = kernel, width,

give.Rkern = FALSE,

n = 512, from, to, cut = 3, na.rm = FALSE, ...)

Обязательные параметры: выборка, ядро, используя параметр kernel. Так же можно указать критерий по параметру сглаживания или его численное значение - параметр bw = "nrd0", (другие. так же указывать как строковую константу. nrd, ucv, bcv, SJ).

ecdf(x)

На вход только выборку.

Также добавив приставку d – плотность или p – функция распределения, можно получить соответственно плотность или функцию распределения указанного после приставки закона распределения:

pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
dunif(x, min = 0, max = 1, log = FALSE)