Решение задач организации СД

Распределение значений критерия организации по СЕ. В тех случаях, когда ОД состоит из нескольких частей (структурных единиц), возникает задача распределения значений критерия организации СД по отдельным СЕ. Это может быть осуществлено по степени сложности СЕ, определяемой рангом сложности, который рассчитывается с помощью матрицы сложности. Матрица сложности А_сл представляет собой квадратную матрицу с числом строк (столбцов), равным числу СЕ. Матрица заполняется в ходе сравнения по сложности отдельных СЕ в соответствии со следующим правилом: если СЕ равна сложности или сложнее сравниваемой СЕ, то всоответствующем месте ставится 1, в противном случае – 0, А_сл = [a_ij], 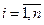; ; 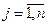n – число СЕ.

Для количественной оценки вводится понятие ранга сложности

, (14.7)

где b_ij – элемент квадрата матрицы А_сл., который получается следующим образом:

; .

Показатель готовности сложного объекта П_г определяется через показатели готовности СЕ

,

откуда

Пример. Объект диагностирования - электростанция состоит из четырех СЕ: СЕ 1, СЕ 3 кабельная сеть и генератор, СЕ 2 – регулятор напряжения, СЕ 4 – РЩ. Показатель готовности ЭС П_г=0.9.

Необходимо распределить показатель готовности по структурным единицам. Известно, что СЕ 1 и СЕ 3 одинаковы по сложности, СЕ 2 сложнее СЕ 1 и СЕ 3; СЕ 4 – самая сложная СЕ.

Составим матрицу сложности и возведем ее в квадрат

;

В соответствии с (14.7)

R_сл1 = R_сл3 = 4/26; R_сл2 = 7/26; R_сл4 = 11/26 и, следовательно,

; ;

; ;

; .

Выбор вида диагностирования. При диагностировании ЭУ, состоящих из нескольких СЕ, возникает вопрос об организации их диагностирования. Отдельные СЕ ЭУ могут диагностироваться последовательно (рис.14.11) или параллельно (рис.14.12) во времени. В некоторых случаях целесообразно разделить все СЕ объекта на группы, и тогда группы можно диагностировать последовательно (рис.14.13), а блоки, входящие в одну группу, параллельно (последовательно-параллельное диагностирование) или группы – параллельно (рис.14.14), а блоки, входящие в одну группу, – последовательно (параллельно-последовательное диагностирование).

Такое диагностирование называется смешанным. При этом целесообразно определить число каналов диагностирования СД, которое обеспечит заданный показатель готовности ОД или время диагностирования не превысит заданного значения.

Задача организации процесса диагностирования формулируется по-разному. Приведем наиболее характерные для ЭУ.

1. Определение минимального числа каналов N_min при условии, что время диагностирования объекта не превысит допустимого значения, т.е. t_д, t_д.доп.

2. Определение минимального числа каналов N_min при условии, что показатель готовности объекта не будет ниже требуемого, т.е. П_г 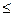П_г.тр.

Подобная задача может быть решена следующим образом. Если ОД непрерывного использования состоит из n СЕ, равноценных по значению, диагностирование осуществляется случайно-периодически идеальными ТСД, а максимальное значение показателя готовности объекта можно определить по формуле:

.

Минимальное число каналов диагностирования определяется следующим образом:

,

причем рассчитанное N_min округляется до большего целого.

Если N_min = 1, то диагностирование последовательное; если N_min = n, то диагностирование параллельное; если 1<N_min<n, то диагностирование смешанное.

При смешанном диагностировании в случае последовательно-параллельной оценки состояния объекта СЕ следует упорядочить по времени диагностирования и компановать в группы так, начиная с СЕ, имеющей наибольшее , чтобы в каждой группе максимальное число СЕ не превышало N_min.

При параллельно-смешанном диагностировании СЕ следует объединить в группы так, чтобы суммы времени диагностирования СЕ в каждой группе были по возможности одинаковыми и не превышали времени диагностирования объекта, т.е.

,

где k, m и r – число СЕ в группе; р – число групп.

Пример. ОД включает восемь СЕ; время диагностирования СЕ составляет в этом случае: ч, 2.5 ч, 0.5 ч, 3 ч, 1.5 ч, 4 ч, 2 ч, 3,5 ч. Интенсивность отказов объекта 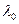= 4∙10^-4 1/ч.

Необходимо организовать процесс диагностирования таким образом, чтобы показатель готовности объекта П_г 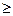0.9. Определим N_min

.

Поскольку 1<N_min<n, необходимо использовать смешанное диагностирование.

Если выбрать последовательно-параллельное диагностирование, то СЕ компонуются в три группы:

1 группа – 4 ч; 3,5 ч; 3 ч;

2 группа – 2.5 ч; 2 ч; 1.5 ч;

3 группа – 1 ч, 0.5 ч.

При этом 7,5 ч, а максимальное значение показателя готовности

.

Следовательно, такая организация процесса диагностирования удовлетворяет поставленным требованиям.

Если осуществить параллельно-последовательное диагностирование, то СЕ следует группировать следующим образом:

1 группа – 0.5 ч, 2.5 ч, 3 ч;

2 группа – 1 ч, t 1.5 ч 3,5 ч;

3 группа – 2 ч, 4 ч.

При этом 6 ч, а максимальное значение П_Г

.

Условие по показателю готовности выполняется.

Если принять параллельное диагностирование, то N_min = 8, 4 ч и П_гmax = 0.927.

При последовательном диагностировании N_min = 1, 18 ч и П_гmax = 0.59.

Сравнив полученные результаты, придем к выводу, что наибольший показатель готовности 0.927 достигается при параллельном диагностировании при 4 ч, однако, при этом необходимо иметь 8 каналов в СД. В связи с этим лучшим вариантом следует признать параллельно-последовательное диагностирование, при котором достигается показатель готовности выше требуемого 0.918 при сравнительно небольшом времени диагностирования 6 ч и требовании наличия только трех каналов в СД.

Контрольные вопросы

1. Выберите из предложенных вариантов ответ на вопрос: Что предполагает организация СД?

Ответы:

а) определение взаимосвязи между элементами СД;

б) определение требований к элементам СД;

в) определение требований к элементам СД и режимам использования диагностирования.

2. Выберите из предложенных вариантов ответ на вопрос: От каких показателей зависит критерий организации СД?

Ответы:

а) объекта и средства диагностирования;

б) объекта и средства диагностирования, ЧО, режимов использования и диагностирования;

б) объекта и средства диагностирования, ЧО, режимов использования и диагностирования, безотказности.

3. Как выглядит целевая функция при решении задач организации СД в случае обеспечения заданного значения критерия организации?

Ответы:

a) ;

б) ;

в) .

4. Чем отличается однородный марковский процесс от полумарковского?

Ответы:

а) мгновенностью перехода из состояния в состояние;

б) показателями перехода из состояния в состояние;

в) показателями состояний.

5. Определите содержание и последовательность действий методики получения выражения для критерия организации СД.

Ответы:

а) определить совокупность состояний СД - построить граф переходов; составить систему уравнений; решить систему уравнений; выбрать состояния, интересующие проектировщика; получить выражение;

б) определить совокупность состояний СД; выбрать состояние, интересующее проектировщика; составить систему уравнений; решить систему уравнений - получить выражение;

в) определить совокупность состояний СД; построить граф переходов - выбрать состояния, интересующие проектировщика ; составить систему уравнений; получить выражение.

6. Определите последовательность действий при построении модели взаимодействия ОД и ТСД.

Ответы:

а) построить временные циклограммы, выделить идентичные состояния, перенумеровать состояния - построить ориентированный граф;

б) определить исходные состояния, построить временные циклограммы, выделить идентичные состояния, построить ориентированный граф;

в) определить исходные состояния, построить временные циклограммы, выделить идентичные состояния, перенумеровать состояния, построить ориентированный граф.

7. Как выглядит критерий сложности, используемый для распределения показателей готовности по СЕ (b_ij – элементы квадрата матрицы сложности)?

Ответы:

а) ;

б) ;

в) .

8. Какой вид диагностирования используется при соотношении 1<N_min<n (n – число СЕ; N_min – минимальное число каналов)?

Ответ:

а) смешанный;

б) только параллельно-последовательный;

в) только последовательно-параллельный.

ГЛАВА 15