Прогнозирование состояния элементов эу
Методы прогнозирования
В исходном состоянии элементы изоляции имеют достаточно высокое пробивное напряжение. Вероятность безотказной работы системы изоляции, рассчитанная по математической модели, обычно близка к единице. В результате износа электроизоляционных материалов при эксплуатации пробивное напряжение снижается и соответственно уменьшается вероятность безотказной работы изоляции. Задачей, решаемой в процессе эксплуатации, является прогнозирование этого изменения.
Можно экспериментально изучить зависимость параметров распределения пробивного напряжения от времени воздействия эксплуатационных факторов, которая выражается в аналитическом виде, например, в виде полинома. По формуле определяются параметры распределения пробивного напряжения в любой момент времени, а при помощи математической модели рассчитывается вероятность безотказной работы элементов изоляции и прогнозируется срок безотказной работы. Это осуществимо при наличии достаточного количества экспериментального материала и при условии воспроизводимости экспериментов.
При недостаточности экспериментальных материалов и трудновоспроизводимых условий опытов используются другие методы. Обозначим через U(t) пробивное напряжение в момент времени t. Изменения U(t) во времени обуславливаются как внешними факторами, так и ходом физических процессов, протекающих внутри изоляции. Вид реализации U(t) зависит от начального состояния изоляции, например, от технологии изготовления. Можно предположить, что зависимость пробивного напряжения от времени линейна, т.е.
 . (13.1)
. (13.1)
Это достаточно приемлемо в связи с тем, что, как правило, при другой зависимости U(t) можно найти преобразование, приводящее имеющуюся зависимость к виду (13.1).
Для каждого элемента изменение U(t) носит определенный, неслучайный характер. Случайность в изменении U(t) состоит в том, что коэффициент 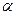 в уравнении (13.1) является случайной величиной, определяемой начальным состоянием элемента. Очевидно, что
в уравнении (13.1) является случайной величиной, определяемой начальным состоянием элемента. Очевидно, что 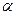 есть скорость изменения U(t):
есть скорость изменения U(t):
 .
.
Достаточно точно скорость изменения параметра можно представить в виде
 ,
,
где V(t) – некоторая детерминированная функция;  – случайный процесс.
– случайный процесс.
Не нарушая общности, принимается, что математическое ожидание процесса  является величиной постоянной и равной 1, т.е.
является величиной постоянной и равной 1, т.е.
 .
.
При этом математическое ожидание скорости x(t) задается равенством
 .
.
Износ, накопленный к моменту времени t, записывается уравнением вида:
 ,
,
где U(0) – пробивное напряжение в начальный момент времени.
Он равен интегралу от скорости износа:
 .
.
Математическое ожидание износа есть интеграл от математического ожидания скорости износа
 .
.
В частности, если  ,
,
где a, b – постоянные,
то математическое ожидание износа будет определено равенством  , т.е. износ в среднем растет как логарифм времени.
, т.е. износ в среднем растет как логарифм времени.
Если рассмотреть идеализированные модели процессов изменения пробивного напряжения, то получатся различные распределения времени безотказной работы. Наиболее подходящими для нашего случая являются следующие модели. Пусть средняя скорость износа постоянна, начальное качество элементов полностью однородно, скорость износа подвержена случайным вариациям. В этом случае можно показать, что время безотказной работы будет иметь гамма-распределение. Плотность этого распределения имеет следующий вид:
 , (13.2)
, (13.2)
где  и
и 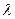 – постоянные параметры; Г(r) – гамма-функция, определяемая формулой:
– постоянные параметры; Г(r) – гамма-функция, определяемая формулой:
 .
.
Если постепенное накопление повреждений не является прямой причиной отказа, а приводит лишь к увеличению его вероятности, то время безотказной работы распределено по закону Вейбулла-Гнеденко, плотность которого имеет вид:
 , (13.3)
, (13.3)
где 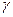 и
и  – постоянные параметры.
– постоянные параметры.
Постоянные параметры в формулах (13.2) и (13.3) определяются в результате эксперимента.
При рабочем напряжении во внутренней изоляции электрооборудования могут развиваться процессы электрического старения. Установлено, что такое старение имеет место при напряжениях электрического поля, во много раз меньших (в 5 раз и более) пробивных напряженностей, измеренных при кратковременном приложении напряжения.
С увеличением напряжения, приложенного к изоляции любого типа, темпы электрического старения возрастают, а сроки службы соответственно уменьшаются. Зависимость срока службы  от значения воздействующего напряжения U в широком диапазоне значений
от значения воздействующего напряжения U в широком диапазоне значений  может иметь сложный характер. Для области относительно малых сроков службы (от единиц до 104 ч) экспериментально установлена зависимость следующего вида:
может иметь сложный характер. Для области относительно малых сроков службы (от единиц до 104 ч) экспериментально установлена зависимость следующего вида:
 , (13.4)
, (13.4)
где А – постоянная, значение которой зависит от свойств изоляции; n – показатель степени, зависящий от конструктивных особенностей изоляции и рода воздействующего напряжения.
Например, для бумажно-масляной изоляции с резко неоднородным электрическим полем (конденсаторного типа) при напряжении промышленной частоты n = 4–8, а при постоянном напряжении n = 9–12; для масляно-барьерной изоляции со слабо неоднородным электрическим полем n 50–80.
График зависимости  , соответствующий формуле 13.4, построенный в двойном логарифмическом масштабе, т.е.
, соответствующий формуле 13.4, построенный в двойном логарифмическом масштабе, т.е.  , имеет вид прямой (рис.13.1, кривая 1). Традиционно при построении таких зависимостей оси ординат откладывают
, имеет вид прямой (рис.13.1, кривая 1). Традиционно при построении таких зависимостей оси ординат откладывают  , а по оси абсцисс –
, а по оси абсцисс –  .
.
 Для области больших сроков службы (более 104 часов) количество экспериментальных данных сравнительно невелико из-за большой зависимости и продолжительности экспериментов, поэтому ход зависимости t=f(U) в этой области определен с меньшей достоверностью. Тем не менее установлено, что по мере снижения напряжения U сроки службы в этой области увеличиваются быстрее, чем следует из 13.4, а ниже некоторого напряжения становятся неограниченно длительными (рис 13.1, кривая 2).
Для области больших сроков службы (более 104 часов) количество экспериментальных данных сравнительно невелико из-за большой зависимости и продолжительности экспериментов, поэтому ход зависимости t=f(U) в этой области определен с меньшей достоверностью. Тем не менее установлено, что по мере снижения напряжения U сроки службы в этой области увеличиваются быстрее, чем следует из 13.4, а ниже некоторого напряжения становятся неограниченно длительными (рис 13.1, кривая 2).
Такому ходу зависимости  качественно соответствует выражение
качественно соответствует выражение
 , (13.5)
, (13.5)
где Uч.р. – напряжение появления в изоляции частичных разрядов, является основной причиной электрического старения внутренней изоляции.
Интенсивность процесса электрического старения любой изоляционной конструкции зависит не только от значения воздействующего напряжения, но и от ряда факторов, не поддающихся контролю, например, от количества, размеров и расположения микронеровностей на поверхностях электродов. Поэтому срок службы изоляционной конструкции любого типа при заданном напряжении является величиной случайной. Для описания  как величины случайной обычно используют функцию распределения Вейбулла
как величины случайной обычно используют функцию распределения Вейбулла
 , (13.6)
, (13.6)
где b – параметр масштаба, численно равный сроку службы при вероятности отказа 0.632; с – параметр формы, зависящий только от стандарта распределения.
Параметр b в (13.6) пропорционален среднему значению ( математическому ожиданию) т.е.
 , (13.7)
, (13.7)
где kb – коэффициент, зависящий от параметра с (при с=10–15, kb=1.03–1.05). Поэтому, используя (13.4), можно написать
 . (13.8)
. (13.8)
Выражение (13.8) используется при статистическом анализе опытных данных о сроках службы, при оценке допустимых для изоляции рабочих напряжений или напряженностей.
Большие разбросы сроков службы, наблюдаемые в опытах с одинаковыми конструкциями, существенно усложняют задачу правильной оценки сроков службы при заданном напряжении. Дело в том, что опыты с крупногабаритными изоляционными конструкциями стоят очень дорого и требуют больших затрат времени. Поэтому, как правило, удается испытать малое количество таких конструкций, а при небольшом объеме опытных данных параметров в (13.8) получаются весьма приближенными.
Таким образом, имеется ряд формул, которые в различных случаях могут являться математическими моделями состояния изоляции, т.е. выражениями, связывающими время и вероятность безотказной работы с определенными параметрами изоляции. Выяснить, какая из этих моделей адекватна исследуемой изоляции, можно экспериментальными методами, после чего – использовать модель для прогнозирования состояния изоляции электроэнергетического оборудования.
