Выбор закона распределения наработок до отказов

Для определения вида закона распределения по статическим данным строят гистограмму. Гистограмма – график статистической плотности распределения случайной величины в виде ступенчатого многоугольника. Строится она следующим образом: на оси абсцисс откладываются интервалы 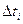. На каждом из них строится прямоугольник с ординатой, равной значению одного из показателей надежности (рис.4.2). Соединив ординаты середины интервалов 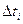, получают полигон соответствующего показателя (кривая статистической плотности). Сравнивая по внешнему виду опытные кривые с соответствующими теоретическими кривыми с учетом характера возникновения отказов, принимают гипотезу о предполагаемом законе распределения.

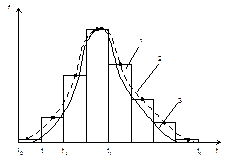
Проверку допустимости принятого теоретического закона (согласованность экспериментальной и теоретической кривых) проводят по различным критериям согласия, из которых наиболее распространенными являются критерий Колмогорова и критерий 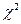(хи-квадрат) Пирсона. Первый используется в случае, когда параметры распределения известны до опыта и требуется после опыта лишь проверить согласованность теоретического и экспериментального распределений, второй – при неизвестных параметрах распределения случайной величины.

Алгоритм применения критерия 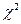при оценивании согласия теоретического и статистического распределений с учетом известных значений статистических частот 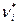(см. табл.4.3.) предполагает:

1. Определение меры расхождения

,

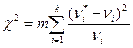где 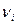– теоретическая частота; 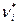– статистическая частота случайной величины в i-м интервале; к – число интервалов; m – объем выборки.

2. Нахождение числа степеней свободы

r = к - (s + 1),

где s – число параметров теоретического распределения.

Теоретическая частота и число степеней свободы зависят от вида принятого теоретического закона распределения (табл.4.3).

3. Определение вероятности согласия Р.

Вычисленные значения 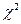сравнивают с табличными значениями (табл.4.4),соответствующими доверительной вероятности 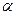= (0,9; 0,95; 0,99; 0,999). Если табличное значение больше вычисленного, гипотезу принимают, в противном случае – отвергают.

Проиллюстрируем реализацию алгоритма аппроксимации опытных данных нормальным распределением. В этом случае плотность вероятности отказа, вероятность отказа и вероятность отсутствия отказа определяется следующим образом:

,

,

,

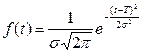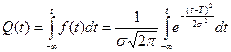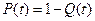где Т – математическое ожидание наработок до t_i, 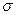– среднеквадратичное отклонение наработки от среднего значения Т.

Условные обозначения: Ф – функция Лапласа; х_i – начальное значение случайной величины в i-й выборке; x_i+1 – конечное значение случайной величины в i-й выборке.

Функция 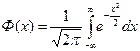табулирована в литературе [3].

Очевидно, что .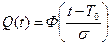

Таблица 4.3