Расчет показателей надежности элементов эу

ПРИ ПРОЕКТИРОВАНИИ

Общие положения

Расчет надежности позволяет получить количественные значения показателей надежности ЭУ. В зависимости от условий, в которых выполняется расчет надежности, и специфики ЭУ определяются различные количественные показатели. Расчет надежности может быть сведен к решению одной из двух типовых задач, сформулированных ниже.

1. Определение надежности существующих ЭУ с целью нахождения количественных показателей надежности. Для этого необходимо знать количественные показатели основных и резервных элементов и их функциональные связи, а также количественные характеристики системы обслуживания. Полученные результаты могут быть использованы для совершенствования технических решений и повышения эффективности ЭУ за счет правильной организации эксплуатации.

2. Определение надежности разрабатываемых ЭУ с целью выявления оптимальной структуры, а также количественных показателей надежности элементов, обеспечивающих требования по надежности ЭУ. Для этого необходимо знать функциональные связи между элементами, требования к надежности ЭУ и ограничения, накладываемые на массу, габариты, стоимость, обслуживание и др. Полученные результаты могут быть использованы для выбора элементов и способов их соединения. Расчет надежности ведется по структурной схеме с использованием аналитических зависимостей между исходными данными и конечным результатом. Порядок расчета надежности следующий.

1. Формулируется понятие отказа. При этом необходимо учитывать только те элементы, выход из строя которых приводит к отказу ЭУ.

2. Составляется схема расчета так, чтобы элементами расчета были конструктивно оформленные блоки.

3. Выбирается метод расчета надежности, степень достоверности расчета зависит от принимаемых допущений при выборе величины интенсивности отказов li и от полноты учета факторов, влияющих на надежность ЭУ.

4. Составляется таблица интенсивностей отказов элементов ЭУ. Для этого используются специальные табличные формы, в которые записываются сведения об элементах и данные их надежности.

5. Производится расчет вероятности безотказной работы элементов ЭУ в зависимости от времени работы и строятся соответствующие графики.

6. Вычисляется средняя наработка до отказа Т_ср.

7. Вычисляются остальные количественные показатели надежности, необходимые для характеристики элементов ЭУ.

Расчет надежности восстанавливаемого и невосстанавливаемого оборудования при различном соединении элементов можно осуществлять с использованием математического аппарата теории вероятностей. Ниже приводятся типовые случаи расчета надежности, которые часто встречаются в инженерной практике.

Расчет показателей безотказности невосстанавливаемых

Элементов ЭУ

Основным свойством надежности невосстанавливаемого оборудования является безотказность. Показателями безотказности невосстанавливаемого оборудования могут быть: вероятность безотказной работы, вероятность отказа, интенсивность отказа, средняя наработка до отказа. Наиболее распространенный вид соединений элементов электрооборудования последовательное, называемое основным. При расчете надежности элементов ЭУ имеющей, основное соединение элементов, принимают допущение, что отказ элемента является случайным и независимым. Это допущение, если режимы работы элементов не изменяются до отказа ЭУ, соответствует действительности. Так как при отказе хотя бы одного элемента происходит отказ всей ЭУ, интерес представляет лишь первый отказ элемента, независимо от того, в каком состоянии будут остальные элементы.

Исходными данными для расчета безотказности являются значения показателей безотказности элементов.

Вероятность безотказной работы при основном соединении элементов равна произведению вероятностей безотказной работы отдельных элементов в течение того же времени

,

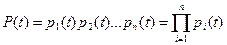где 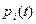- вероятность безотказной работы i-го элемента.

Соответственно вероятность отказа оборудования при основном соединении элементов

.

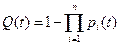Интенсивность отказов 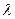при основном соединении элементов равна сумме интенсивностей отказов отдельных элементов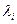

.

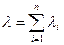Средняя наработка до отказа

.

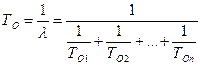При n = 2 .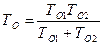

Расчет безотказности ЭУ при резервном соединении элементов ведется следующим образом. Поскольку при общем резервировании отказ ЭУ наступит при отказе всех резервных и одного основного, то при наличии резервных цепей вероятность отказа ЭУ будет равна произведению вероятностей отказа основной и резервной цепей

.

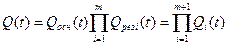Если вероятности отказов всех резервных элементов одинаковы, то вероятность отказа ЭУ

.

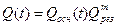На практике вероятности отказов основных и резервных элементов обычно оказываются одинаковыми, поскольку в качестве резервных выбираются такие же, как и основные. При этом вероятность отказа ЭУ будет равна 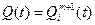и, следовательно, вероятность безотказной работы

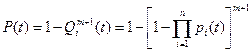, (3.1)

где n – число элементов в основной или резервной цепи;

m – число резервных цепей.

Тогда вероятность отказа ЭУ при общем резервировании

.

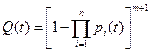При равенстве вероятностей безотказной работы всех элементов ЭУ

;

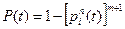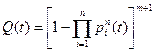. (3.2)

Для большого числа практических случаев характерен экспоненциальный закон распределения времени отказов.

Поскольку для экспоненциального закона распределения

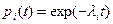
то, 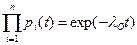, где .

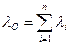В этом случае выражения 3.1 и 3.2 примут вид

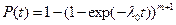и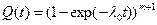

Средняя наработка до отказа при общем резервировании ЭУ

.

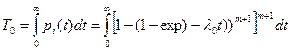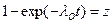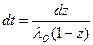Если обозначить , то и

.

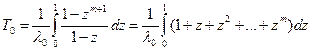Обозначив 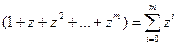, получим

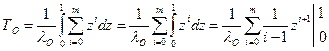
или 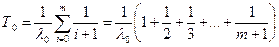. (3.3)

Интенсивность отказов ЭУ при общем резервировании будет равна

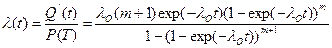. (3.4)

Для высоконадежных объектов справедливы соотношения 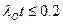и 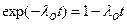и выражения для показателей безотказности будут следующими:

; ; ;

.

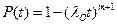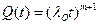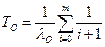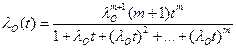При общем резервировании с дробной кратностью m=(l-h)/n, где l – общее число основного и резервного оборудования; h – число оборудования, необходимого для нормальной работы, вероятность безотказной работы

,

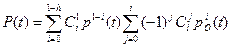где 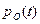– вероятность безотказной работы основного или любого резервного оборудования.

При раздельном резервировании, если каждый основной элемент имеет m резервных элементов, вероятность отказа ЭУ из-за отказа элементов i-го типа будет равна произведению вероятностей отказов i-го элемента и всех элементов, ее резервирующих, т.е.

.

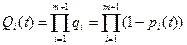Вероятность безотказной работы i-го элемента и всех его резервных при этом будет

.

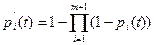Поскольку на практике основные и резервные элементы имеют одинаковую вероятность безотказной работы, то

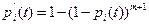. (3.5)

Так как элементы (основной и резервные) имеют основное соединение, вероятность безотказной работы оборудования при раздельном резервировании

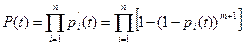. (3.6)

Если вероятность безотказной работы всех элементов будут равны, то

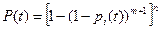. (3.7)

На практике вычисления по (3.6) выполняются следующим образом:

вычисляются по (3.5) вероятности безотказной работы элементов 1, 2, ..., i-го типов, причем ;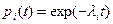

полученные значения вероятностей для каждой группы элементов перемножаются и определяется Р(t);

по вероятности Р(t) определяют все показатели безотказности.

Анализ упрощается, если безотказность высока и вероятность безотказной работы при любых t превышает 0.9. При этом допущении

.

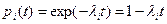В этом случае, если все элементы равнонадежны, то

.

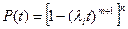Для высоконадежных элементов следует рассматривать средневзвешенную интенсивность отказов элементов:

,

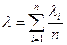из которых состоит ЭУ.

Отсюда найдем количественные показатели безотказности ЭУ

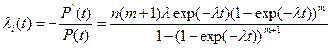
и для высоконадежных элементов

,

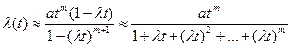где .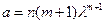

Если элементы резервированной ЭУ могут иметь два вида отказов – обрыв и короткое замыкание, то вероятность безотказной работы следует определять как сумму вероятностей возникновения благоприятных ситуаций, т.е. не приводящих к отказу ЭУ,

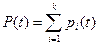(3.8)

где 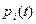– вероятность i-й благоприятной ситуации, k – число благоприятных ситуаций.

Если резервные элементы подключаются только в случае отказа основных элементов (осуществляется резервирование замещением), то вероятность безотказной работы ЭУ определяется по формуле

,

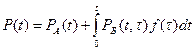где 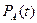– вероятность безотказной работы основных элементов;

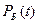– вероятность безотказной работы резервных элементов за промежуток времени 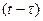при условии, что до момента они были работоспособны; 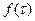– функция распределения вероятности отказа ЭУ. ЭУ с кратностью резервирования m может быть заменено ЭУ, имеющей кратность резервирования (m-1) с дополнительной одной резервной ЭУ.

Тогда вероятность безотказной работы

.

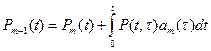где 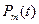– вероятность безотказной работы ЭУ, резервированной (m-1) раз в течение времени t; 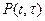– вероятность безотказной работы одной резервной ЭУ в течение времени 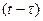при условии, что до момента она работоспособна; 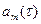– функция распеределения вероятности времени повреждения ЭУ с кратностью резервирования (m-1).

Примеры расчета показателей безотказности