Предельные теоремы в схеме Бернулли.

Итак, мы рассматривает вопрос о вероятности некоторого числа успехов в серии испытаний Бернулли заданной длины. Для нахождения этой вероятности мы используем формулу Бернулли. Рассмотрим теперь такую задачу:

Вероятность появления события А в каждом из 900 независимых испытаний равна р = 0,8. Найти вероятность того, что событие А про изойдет: а) 750 раз; б) Число успехов будет в промежутке от 700 до 750 раз. Очевидно, что использование формулы Бернулли здесь затруднительно.

Трудности возрастают, когда приходится суммировать вероятности 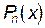для ответа на второй вопрос.

Определение 19.2.1. В отдельных случаях при больших n удается заменить формулу Бернулли приближенными формулами. Такие формулы, которые получаются при условии 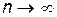, называются, асимптотическими. Соответствующие утверждения называют Предельными теоремами в схеме Бернулли. Мы рассмотрим три таких теоремы: Локальную и интегральную теоремы Муавра-Лапласа и теорему Пуассона.

Замечание 19.2.1. Теоремы, которые теперь носят имя Муавра и Лапласа были доказаны этими учеными независимо, А.де Муавр доказал эти утверждения несколько раньше, но его результаты оставались неизвестными и были обнародованы относительно недавно. Поэтому в разных учебниках эти теоремы могут называться теоремами Лапласа, Муавра-Лапласа, Муавра или просто предельными теоремами в схеме Бернулли.

Локальная терема Муавра-Лапласа.

1)Теорема применяется при достаточно большом числе испытаний. Чем больше n, тем лучше формула теоремы приближает формулу Бернулли.

2)p и q постоянны в каждом испытании

3)успехов достаточно много, их число растет с ростом n, их вероятность достаточна велика, чем ближе вероятность успеха к ½ , тем лучше приближение к формуле Бернулли

Итак, при выполнении указанных условий вероятность того, что в n испытаниях окажется ровно х успехов приблизительно равно

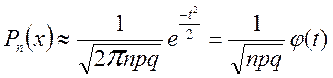, где 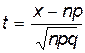, а φ (t) – функция Гаусса.

Здесь: n – число испытаний, х – число успехов

np - (статистически) среднее значение числа появлений х события А при n испытаниях, x–np – соответствующее отклонение

корень из npq – масштабирующий множитель, t – отклонение числа появлений события А от его среднего значения, измеренное в этом масштабе.

Сделаем небольшое отступление и рассмотрим отдельно функцию Гаусса (ее иногда называют локальной функцией Лапласа)

φ (t) = .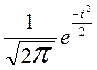

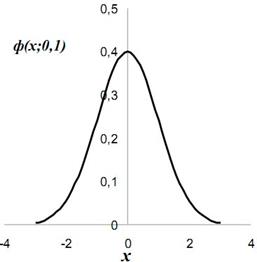
Эта функция обладает следующими свойствами:

1) Функция Гаусса четная, т.е.φ(x)=φ(-x) и ее график, соответственно, симметричен относительно оси y.

2) С ростом (убыванием) х, функция достаточно быстро стремится к нулю. Уже при х=±3,99, φ(х) = 0,0001. При х >4 функция считается равной 0.

3) Для значений функции Гаусса существуют таблицы. Ввиду четности функции они составлены только для положительных значений аргумента..

Итак, чтобы определить вероятность того, что в 50 испытаниях по схеме Бернулли при p=0.45 событие А наступило 30 раз, нужно воспользоваться таблицей значений функции Гаусса, предварительно вычислив значение аргумента t по формуле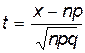

Пример 19.2.1. Вероятность поражения стрелком цели при одиночном выстреле р=0,2. Какова вероятность того, что при 100 выстрелах цель будет поражена ровно 20 раз?

Здесь p=0,2, q = 0,8, n = 100, x= 20, npq = 16

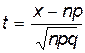= (20-100×0,2):4 = 0

j(0) » 0,4 (точное табличное значение 0,3989)

Р₁₀₀ (20) » 0,4 × ¼ = 0,1

Значение вероятности оказывается маленьким, ведь попадание точно 20 раз при 100 выстрелах – событие достаточно редкое. А попадание «около 20 раз» - будет почти достоверным событием. Так, например, 15£ х £25, включающего 11 значений близка к 1 (можно проверить по формуле Бернулли для суммы по х от 15 до 25 Р₁₀₀ (x)

То есть верно Замечание19.2.1.

Значение конкретной вероятности P_n (x) достаточно мало. Значительно больше оказывается вероятность «около х» успехов, то есть числа успехов, принадлежащего некому промежутку, содержащему х.

Замечание 19.2.2. Так как при | t| ®∞ j(t) монотонно убывает, для одной и той же серии испытаний (n фиксировано) большие отклонения х – np менее вероятны чем меньшие. Это верно для достаточно больших n.

Теперь, допустим, мы хотим оценить вероятность того, что число успехов попадет в промежуток от m₁ до m₂ . Для этого сформулируем