Формула трапеций. Геометрическая иллюстрация. Оценка погрешности Формула трапеций

b

n

Найдем коэффициенты формулы ò f (x) = (b - a)å yi H i

,

a

i=0

где H i =

1 n

(-1)n-i t(t -1)...(t - n)

dt , i=0,1,…,n при n=1.

n ò

i! (n - i)! (t - i)

(-1)1 t(t -1)

æ t 2

ö

ò

ò

ç

÷

При i = 0

H

=

1 0

0!1! t

dt = -

(t -1)dt = -ç

- t

÷

=

è

ø

1 1

(-1)0 t(t -1)

t

При i = 1

H 0

=

ò

dt

=

ò

tdt =

=

1! 0! (t -1)

b

n

Формула ò f (x) = (b - a)å yi H i

на отрезке [x0, x1] примет вид:

a

i=0

x1

æ

1 ö

h

ò f (x)dx =(x - x0)ç y0

+ y1

÷ =

( y0 + y1 )

x0

è

ø

b

æ y

y

ö

Для отрезка [a, b]: ò

n

f (x)dx =hç

+ y1+ y2

+ ... + yn-1 +

÷

(*)

a

è

2 ø

b

b

Рассмотрим погрешность: ò f (x)dx =òLn (x)dx + Rn (x)

a

a

На отрезке [x

, x ]погрешность

R = -

h3

f ¢¢(x ),

x Î[x

, x ] .

0

1

При f ¢¢(x) > 0 (*) дает значение интеграла с избытком; при f ¢¢(x) < 0 (*) дает значение интеграла с недостатком.

На отрезке [a, b] R = -

h3 n

f ¢¢(x ),

x Î[a, b] .

n

b - a

h2

M =max

¢¢

Поскольку hn=|b-a|, то

, где

.

Rn

£ M

xÎ[a,b]

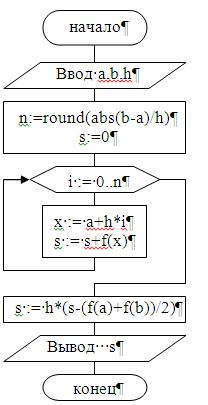
Программа численного интегрирования методом трапеций:

program lab_4_1a;

var i,n :integer;

s,h,a,b,x :real;

function f(x: real):real;

begin {функция в виде f:=[математическое выражение]} f:=sin(x); end; begin

write('Введите левую и правую границы отрезка - '); readln(a,b); write('Введите шаг - '); readln(h); n:=round(abs((b-a)/h));

s:=0;

for i:=0 to n do

begin

x:=a+h*i;

s:=s+f(x);

end;

s:=h*(s-(f(a)+f(b))/2);

writeln('Искомый определенный интеграл равен ',s:10:6); readln;

end.