I.II. Асимптотический метод расчета пластин

Для прямоугольной пластины с закреплением, отличным от шарнирного опирания, по противолежащим сторонам, применяют различные приближенные методы. Рассмотрим асимптотический метод.

В пластинках, так же как и в балках, имеет место динамический краевой эффект, который заключается в том, что закрепление влияет на форму колебания только вблизи границы, а вдали от нее форма колебания определяется произведением синусов. Благодаря этому колебания можно представить как сумму функции гармоник и быстро затухающих с удалением от границ функций, которые позволяют выполнить граничные условия.

Рассмотрим применение этого метода на примере заделанной по контуру прямоугольной пластины размерами , у которой, как и ранее, размер а соответствует оси x. Ограничимся расчетом симметричных относительно осей форм колебаний. В средней части пластины (начало координат располагается в центре тяжести пластины) принимаем

Вблизи границ :

где - быстро изменяющаяся функция, позволяющая удовлетворить условиям закрепления.

Аналогично вблизи границ :

Таким образом, общее выражение для имеет вид

В средней части пластинки функции и пренебрежимо малы и поэтому первый член выражения должен удовлетворять уравнению колебаний. Отсюда находим

Вблизи границ существенными являются первый и второй члены выражения. Учитывая, что первый член удовлетворяет уравнению, потребуем, чтобы и второй удовлетворял ему:

Выполняя дифференцирование, приходим к уравнению:

которое распадается на два уравнения:

Так как , то затухающие решения имеет только первое из этих уравнений. Решение, затухающее с удалением от стороны , имеет вид

где

В силу симметрии вблизи стороны :

Аналогично вблизи стороны :

где

и вблизи стороны :

Рассмотрим граничные условия при :

При вычислении и учтем, что практически вдоль всей стороны , за исключением окрестностей угловых точек, функция равна нулю, поэтому определяется первыми двумя слагаемыми выражения:

Для одновременного выполнения этих уравнений необходимо, чтобы определитель, составленный из коэффициентов при и 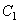, равнялся нулю, что приводит к уравнению:

Аналогично условия при приводят к уравнению:

Так как связаны с , то определяем значения и , а затем вычисляем и частоты:

Рассмотрим, например, колебания квадратной пластинки с одинаковым числом узловых линий в направлениях . В этом случае и уравнения приводят к зависимости:

,

откуда

Частоты колебаний определяются формулой:

Достаточно хороший результат получается уже для низшей частоты:

Точное значение:

Как видно из вышеизложенного, при использовании асимптотического метода погрешность возникает вследствие приближенного выполнения граничных условий вблизи угловых точек.