Регрессионный анализ. Парный. Множественный.
Для обработки результатов эксперимента очень удобно применить регрессионный анализ.
Регрессионный анализ заключается в исследовании распределения коэффициентов регрессии, определяющих случайную величину как функцию от нескольких других. Определение неизвестных коэффициентов регрессии и дисперсии осуществляется методом наименьших квадратов. Регрессионный анализ определяет зависимость между случайной и неслучайными величинами. Регрессионный анализ связан с корреляционным. Регрессионный анализ применяется для исследования поведения коэффициентов весомости при комплексной оценке качества продукции.
С помощью регрессионного анализа можно обнаружить и описать связь между выходным фактором и одним или несколькими входными факторами. В регрессионном анализе мы подбираем модели или функции распределения под наблюдаемые данные. В зависимости от данных это могут быть различные функции.
Цель анализа состоит в подборе линии и создании уравнения, которые объясняют и предсказывают развитие процесса в будущем. Существует множество методов получения аналитической формулы, максимально полно описывающей зависимость эмпирических данных, полученных из практических измерений. Это методы - подгонка линии, наименьших квадратов, частных наименьших квадратов, логистическая регрессия, пошаговая регрессия и т.д.
Регрессионный анализ бывает парный и множественный.
Парный анализ. Достаточно прост, здесь необходимо получить аналитическую формулу зависимости одной функции от одного независимого аргумента
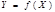
В большинстве случаев уравнение, описывающие с максимальной точностью нашу линию тренда, можно записать как полиноминальное уравнение регрессии:
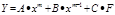
A, B, C, …,D, E, G, F – коэффициенты регрессии. Задача анализа определить эти коэффициенты. Часть коэффициентов может равняться нулю. Если не равны нулю коэффициенты G и F, уравнение регрессии выглядит как, линейное уравнение:
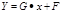
Если не равны нулю коэффициенты E, G и F, уравнение регрессии будет квадратическим и т.д.
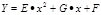и т.д.
Очень эффективно применение специальных компьютерных программ и пакетов. Наиболее доступен пакет EXCEL, а именно построение точечных диаграмм ( диаграмм разброса), определение максимально приближенного тренда и определение аналитической формулы тренда. Все расчеты компьютер делает сам. Программа расчета вложена разработчиками EXCEL.
EXCEL позволяет сразу получить аналитическую формулу максимально , описывающую траекторию тренда и коэффициент детерминации. После получения линии тренда, для получения аналитического выражения и коэффициента детерминации в разделе «параметры» необходимо поставить метки в соответствующие квадратики.
Множественный анализ. Этот анализ определяет аналитическое выражение функции нескольких аргументов. Методика его проведения более сложна и также может проводиться с помощью EXCEL.
Обычно уравнение множественной регрессии выглядит следующим образом - это уравнение линейной регрессии.
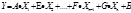
Также , исследуемый процесс может описываться экспоненциальным уравнением:
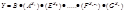
Задача исследования найти значения коэффициентов при Х и свободного члена В. В программе EXCEL есть специальные программы для решения этой задачи. Это программа ЛИНЕЙН(известные значения y; известные значения x; конст; статистика), которая определяет значения в уравнении (10.17.) и программа ЛГРФПРИБЛ(известные значения y; известные значения x; конст; статистика) для уравнения (10.18.). В программу вводят известные значения функции Y, затем известные значения аргумента Х, затем значение – конст, которое может принимать два значения: «ИСТИНА» - в этом случае в уравнении регрессии будет присутствовать значение свободного члена В, «ЛОЖЬ» - свободного члена В не будет, значение – статистика, оно также имеет два значения : «ИСТИНА» - определяются значения ошибок для коэффициентов и свободного члена, «ЛОЖЬ» - значения не определяются. В таблице 8.18. показано размещение полученных данных расчета.
Статистические методы. Параметры статистической совокупности – среднее арифметическое, размах, среднее квадратическое отклонение, среднее квадратическое отклонение среднего значения, закон распределения.
Статистические методы — математические методы описания и изучения массовых явлений, допускающих количественное выражение. Термин «статистика» от итальянского «stato» - государство. Статистика возникла как часть науки управления обществом и означала сбор данных о некоторых параметрах жизнедеятельности государства. Со временем статистика стала охватывать сбор, обработку и анализ данных о массовых явлениях вообще. Сейчас статистические методы охватывают собою практически все области науки и техники.
Центр группирования. Одной из основных характеристик статистической совокупности, дающей представление о том, вокруг какого центра группируются все значения, является среднее арифметическое. Оно определяется из выражения:
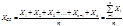
Величина рассеяния. Статические совокупности могут иметь близкие или даже одинаковые значения центра группирования, но отдельные значения величин в них могут существенно отличаться, вследствие того, что разброс значений относительно центра бывает разный. Самой элементарной характеристикой рассеяния является вариационный размах R, определяемый по формуле
R=Xmax - Xmin
где Xmax, Xmin – максимальное и минимальное значения статистической совокупности.
Показателем отклонения значения самого среднего арифметического является среднее квадратическое отклонение среднего значения S, которое еще называют среднее квадратическое отклонение результата измерения или стандартной ошибкой.
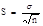
Форма распределения вероятности. Важнейший параметр статистической совокупности. Форма распределения зависит от характера и особенностей выполнения процесса, при котором получается совокупность. В производственном процессе достаточно часто проявляется нормальное распределение. Однако нормальное распределение не является единственно возможным. В зависимости от физической природы случайных величин, некоторые из них на практике могут иметь распределение другого вида, например, логарифмическое, экспоненциальное, Вейбулла, Симпсона, Релея, равной вероятности, треугольное и т.д.