Глава 2. Решение нелинейных уравнений
Отделение корней уравнения
Пусть дано уравнение, которое в общем виде записывается формулой
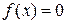 , (2.1)
, (2.1)
где f(x) любая действительная функция.
Точным корнем уравнения (2.1) на конечном или бесконечном отрезке [α,β] назовем всякое число ξ из промежутка, которое обращает функцию.f(x) в нуль. Так как уравнение может быть достаточно сложным, редко удается найти его точные корни. Задача состоит в том, чтобы найти приближенные корни и оценить, насколько точно это сделано.
Процесс нахождения приближенных корней уравнения общего вида f(x) = 0 проводится в два этапа:
1. Отделение корней, то есть установление возможно малых промежутков 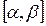 , в которых содержится один и только один корень уравнения (2.1);
, в которых содержится один и только один корень уравнения (2.1);
2. Уточнение приближенных корней.
Если ξ-точный корень, x приближенный корень уравнения (2.1), а ε точность, то для того, чтобы приближенный корень x был найден с заданной точностью ε достаточно потребовать выполнения неравенства: 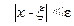 .
.
Теорема 2.1: Если непрерывная функция 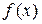 принимает значения противоположных знаков на концах
принимает значения противоположных знаков на концах 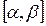 , т.е.
, т.е. 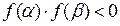 , то внутри этого отрезка содержится, по меньшей мере, один корень уравнения
, то внутри этого отрезка содержится, по меньшей мере, один корень уравнения 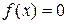 .
.
Корень 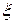 [
[ 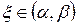 ] заведомо будет единственным, если производная
] заведомо будет единственным, если производная 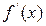 существует и сохраняет постоянный знак внутри интервала
существует и сохраняет постоянный знак внутри интервала 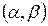 , т.е.
, т.е. 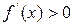 (или
(или 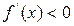 ) при
) при 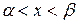 .
.
Аналитический метод отделения корней
Процесс отделения корней начинается с установления знаков функции 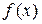 в граничных точках
в граничных точках 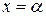 и
и 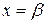 области ее существования. Затем определяются знаки функции
области ее существования. Затем определяются знаки функции 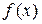 в ряде промежуточных точек
в ряде промежуточных точек 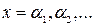 , выбор которых учитывает особенности функции
, выбор которых учитывает особенности функции 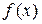 . (Имеются в виду точки, где функция имеет экстремум или разрыв) Если окажется, что
. (Имеются в виду точки, где функция имеет экстремум или разрыв) Если окажется, что 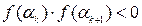 , то в силу теоремы в интервале
, то в силу теоремы в интервале 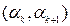 существует корень уравнения
существует корень уравнения 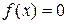 . Можно сузить полученные промежутки методом простой подстановки значений в уравнение.
. Можно сузить полученные промежутки методом простой подстановки значений в уравнение.
Пример2.1. Отделить корни уравнения
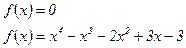
Найдем корни производной

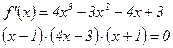 ,
,
 x1=1 x2=0.75 x3=1
x1=1 x2=0.75 x3=1
Составим таблицу. В первой строке поместим в порядке возрастания концы интервала и точки экстремумов, во второй знаки функции в этих точках.
| х | -∞ | -1 | 0.75 | ∞ | |
| Sign f(x) | + | - | - | - | + |
Уравнение имеет два корня. 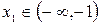 ,
, 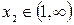 . Уменьшим промежутки, в которых находятся корни:
. Уменьшим промежутки, в которых находятся корни:
| х | -∞ | -2 | -1 | 0.75 | ∞ | ||
| Sign f(x) | + | + | - | - | - | + | + |
Следовательно, 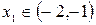 ,
, 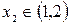 .
.
Графический метод отделения корней
Действительные корни уравнения f(x)=0 можно определить как абсциссы точек пересечения графика функции 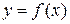 с осью Ох. Если уравнение
с осью Ох. Если уравнение 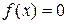 не имеет близких между собой корней, то этим способом корни легко определяются. На практике часто удобно тождественно преобразовать уравнение к виду
не имеет близких между собой корней, то этим способом корни легко определяются. На практике часто удобно тождественно преобразовать уравнение к виду 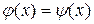 , где
, где 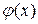 и
и 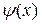 - более простые функции, чем функция
- более простые функции, чем функция 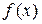 . Тогда, построив графики
. Тогда, построив графики 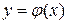 и
и 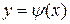 , искомые корни получаются как абсциссы точек пересечения этих графиков.
, искомые корни получаются как абсциссы точек пересечения этих графиков.
Пример 2.2
Отделить графически корни уравнения x·ln(x) -1=0. Преобразуем уравнение к виду 1/x=ln(x) и построим графики.
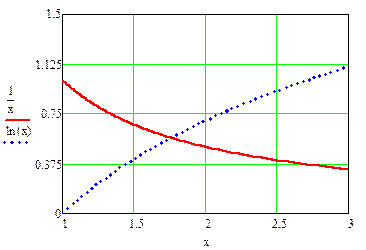 |
Рис 2.1. Графический метод отделения корней
Из графика видно, что 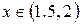 .
.
Уточнение приближенных корней
Метод половинного деления
Пусть уравнение (2.1) имеет на отрезке [a,b] один корень, а функция f(x) на данном отрезке непрерывна и f(a)·f(b)<0. Разделим отрезок [a,b] пополам точкой x1=(а+b)/2. Если f(x1)≠0 , то для продолжения вычислений выберем ту часть промежутка, где знаки функции различны. Концы полученного отрезка обозначим [a1,b1] и снова разделим отрезок [a1,b1] пополам точкой x2=( a1+ b1)/2 и т. д. В результате на каком-то этапе получим или точный корень уравнения(2.1) или бесконечную последовательность вложенных друг в друга отрезков [a1,b1], [a2,b2],… [an,bn],…таких, что
f(an)·f(bn)<0, (n=1,2,…) (2.2)
bn - an=2 -n·(b-a). (2.3)
Так как левые концы a1, a2,… ,an образуют монотонную неубывающую ограниченную последовательность, а правые концы b1 b2,…,bn образуют монотонную невозрастающую ограниченную последовательность, а расстояние между ними в силу (2.2) стремится к нулю, то у последовательностей существует общий предел . Число ξ, которое является общим пределом последовательностей {an} и {bn}, точный корень уравнения (2.1). Оценим погрешность решения на n-м шаге. Считаем до тех пор, пока длина промежутка не станет меньше заданной точности ε.
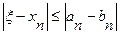
В качестве ответа возьмем середину отрезка [an,bn].
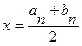 .
.
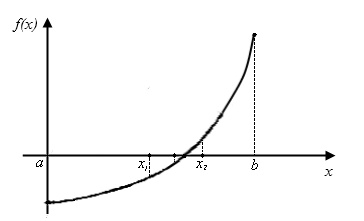
Рис.2.2. К объяснению метода половинного деления
Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, так как при увеличении точности значительно возрастает объём вычислений.
Пример 2.3. Найти, используя пакет Matchcad, методом половинного деления корень уравнения x4-x3-2x2+3x-3=0 на промежутке [1,2]
Функция koren(a,b,ε) возвращает длину отрезка, который будет меньше заданной точности ε, и значение корня на этом промежутке, если на концах отрезка [a,b] функция имеет противоположные знаки, или сообщение об отсутствии корня, в противном случае.
Метод легко реализуется на компьютере. Далее приводится листинг программы, написанной на языке, встроенном в систему Mathcad.
 Рис. 2.3. Листинг программы в Mathcad, реализующей метод половинного деления для примера 2.3
Рис. 2.3. Листинг программы в Mathcad, реализующей метод половинного деления для примера 2.3
Метод хорд
В этом методе нелинейная функция f(x) на отделенном промежутке
[a,b] заменяется хордой, проходящей через точки (a,f(a))и (b,f(b))
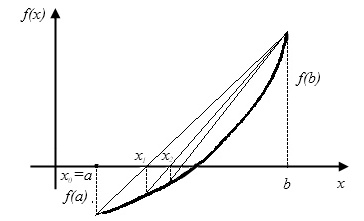
Рис.2.4. Метод хорд. Неподвижен правый конец промежутка b
Уравнение хорды: 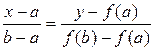 . Найдем точку пересечения хорды с горизонтальной осью. Полагая
. Найдем точку пересечения хорды с горизонтальной осью. Полагая 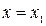 и
и 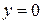 , получим
, получим
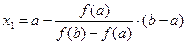 .
.
Точку x1 принимаем за новую границу отрезка, где содержится корень. Через эту точку с координатами (x1,f(x1)) и соответствующую границу предыдущего интервала (b,f(b)) опять проводим хорду, находим 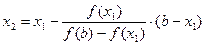 и т.д., получая последовательность x1,x2,x3,…xn,…, сходящуюся к корню уравнения.
и т.д., получая последовательность x1,x2,x3,…xn,…, сходящуюся к корню уравнения.
Вторая производная 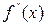 сохраняет постоянный знак на
сохраняет постоянный знак на 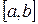 . Следовательно, возможны два случая. Если f(b)·f "(b)>0, то хорда имеет правый фиксированный конец, причем последовательность x0,x1,…xn приближается к корню слева. За начальное приближение x0, естественно, берут a
. Следовательно, возможны два случая. Если f(b)·f "(b)>0, то хорда имеет правый фиксированный конец, причем последовательность x0,x1,…xn приближается к корню слева. За начальное приближение x0, естественно, берут a
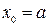 ;
; 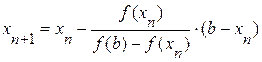 ;
; 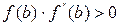 ;
;
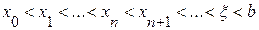 .
.
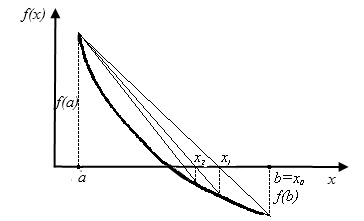
Рис.2.5. Метод хорд. Неподвижен левый конец промежутка a
Если f(a)·f "(a)>0, то хорда имеет левый фиксированный конец, причем последовательность x0,x1,…xn … приближается к корню справа. За начальное приближение x0, берут b
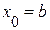 ;
; 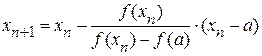 ;
; 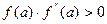 ;
;
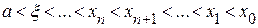 .
.
Для оценки точности можно воспользоваться формулой
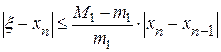 ,
,
где 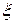 -точный корень,
-точный корень, 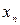 - приближенный корень,
- приближенный корень, 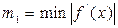 ,
, 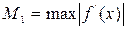 на промежутке [a,b]. Считаем до тех пор пока, не выполнится условие
на промежутке [a,b]. Считаем до тех пор пока, не выполнится условие 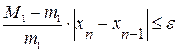 . Если имеет место неравенство
. Если имеет место неравенство 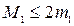 , то счет можно прекратить, когда.
, то счет можно прекратить, когда. 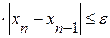
Пример 2.4. Найти методом хорд корень уравнения x4-x-1=0
Решение находим, используя пакет Mathcad.
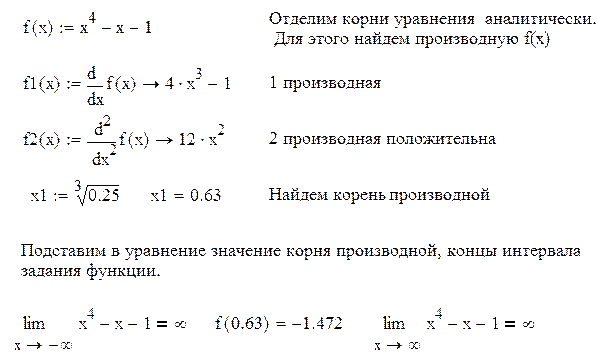
Функция монотонна на промежутках (-∞, 0.63), (0.63, ∞) и меняет на концах промежутков знак. Уравнение имеет два корня. Сузим промежутки отделения корней методом проб, т.е. подстановкой.
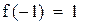 |
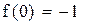 |
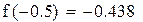 |
Первый корень принадлежит промежутку (-1,-0.5)
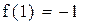 |
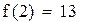 |
Второй корень принадлежит промежутку (1,1.5)
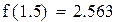 |
Будем находить корень на промежутке (-1,-0.5)
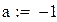 |
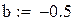 |
Вторая производная всюду положительна, функция положительна в точке a = -1, значит, этот конец неподвижен.
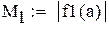 |
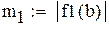 |
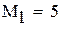 |
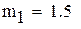 |
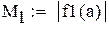 |
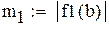 |
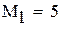 |
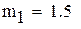 |
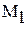 -максимальное, a -максимальное, a 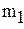 -минимальное значение модуля производной на промежутке -минимальное значение модуля производной на промежутке |
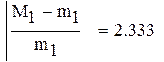 |
так как 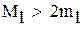 , множитель
, множитель 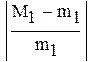
нужно учитывать при оценке точности решения,
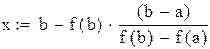 |
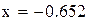 |
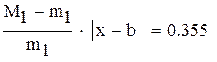 |
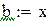 |
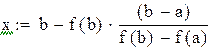 |
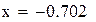 |
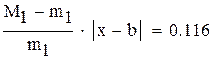 |
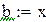 |
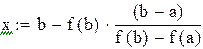 |
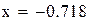 |
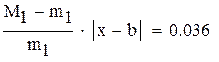 |
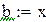 |
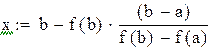 |
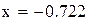 |
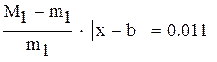 |
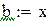 |
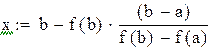 |
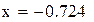 |
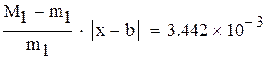 |
Нашли корень исходного уравнения 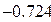 с точностью
с точностью 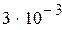 .
.
Рис. 2.6. Вычисления в Mathcad, реализующие метод хорд для примера 2.4
