Глава 1. Погрешность результата численного решения задачи
Глава 1. Погрешность результата численного решения задачи
Источники и классификация погрешностей
Погрешность решения задачи обуславливается следующими причинами:
1) математическое описание задачи является неточным, в частности неточно заданы исходные данные описания;
2) применяемый для решения метод часто не является точным: получение точного решения возникающей математической задачи требует неограниченного или неприемлемо большого числа арифметических операций; поэтому вместо точного решения задачи приходится прибегать к приближенному;
3) при вводе данных в машину, при выполнении арифметических операций и при выводе данных производятся округления.
Погрешности, соответствующие этим причинам, называют:
1) неустранимой погрешностью,
2) погрешностью метода,
3) вычислительной погрешностью.
Часто неустранимую погрешность подразделяют на две части:
а) неустранимой погрешностью называют лишь погрешность, являющуюся следствием неточности задания числовых данных, входящих в математическое описание задачи;
б) погрешность, являющуюся следствием несоответствия математического описания задачи реальности, называют, соответственно, погрешностью математической модели
Дадим иллюстрацию этих определений. Пусть у нас имеется маятник (рис. 1.1.), начинающий движение в момент t = t0 . Требуется предсказать угол отклонения φ от вертикали в момент t1.
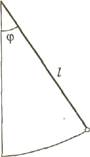
Рис. 1.1. - Маятник
Дифференциальное уравнение, описывающее колебание этого маятника, берется в виде:
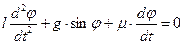 , (1.1)
, (1.1)
где l — длина маятника, g — ускорение силы тяжести, φ — коэффициент трения.
Как только принимается такое описание задачи, решение уже приобретает неустранимую погрешность, в частности, потому, что реальное трение зависит от скорости не совсем линейно; другой источник неустранимой погрешности состоит в погрешностях определения l, g, µ, t0, φ(t0), φ΄(t0). Название этой погрешности — «неустранимая» — соответствует ее существу, она неконтролируема в процессе численного решения задачи и может уменьшиться только за счет более точного описания физической задачи и более точного определения параметров. Дифференциальное уравнение (1.1) не решается в явном виде; для его решения требуется применить какой-либо численный метод. Вследствие этой причины и возникает погрешность метода.
Вычислительная погрешность может возникнуть, например, из-за конечности количества разрядов чисел, участвующих в вычислениях. Введем формальные определения.
Пусть I — точное значение отыскиваемого параметра (в данном случае — реальный угол отклонения маятника φ в момент времени t1), II — значение этого параметра, соответствующее принятому математическому описанию (в данном случае — значение φ(t1) решения уравнения (1.1)),
IIh-— решение задачи, получаемое при реализации численного метода в предположении отсутствия округлений, IIh*—приближение к решению задачи, получаемое при реальных вычислениях. Тогда
Ρ1 = II—I — неустранимая погрешность,
Ρ2 = IIh —I — погрешность метода,
Ρ3 = IIh*—IIh — вычислительная погрешность.
Полная погрешность Ρ0 получается по формуле
Ρ0= Ρ1+ Ρ2+ Ρ3
Абсолютная и относительная погрешности.
Формы записи данных.
Если а — точное значение некоторой величины а, а * — известное приближение к нему, то абсолютной погрешностью приближенного значения а* называют обычно некоторую величину Δ(а*), про которую известно, что
|а* - а| ≤ Δ(а*)
Относительной погрешностью приближенного значения называют некоторую величину δ(а*), про которую известно, что
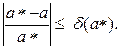
Относительную погрешность часто выражают в процентах. Если а — известное число, например π, то иногда говорят об абсолютной Δ (а) и относительной δ(а) погрешностях задания этого числа: числа Δ(а) и δ(а) называют соответственно абсолютной и относительной погрешностью числа а.
Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой слева.
Пример 1.1. У чисел а* = 0,07045, а* = 0,07045000 значащими цифрами являются подчеркнутые цифры. Число значащих цифр в первом случае равно 4, во втором — 7.
Значащую цифру называют верной в широком смысле, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.
Пример 1.2. а* = 0,06045, Δ(а*)=0,000003;
а* = 0,06045000, Δ(а*)=0,0000007;
подчеркнутые цифры являются верными.
Уславливаются называть значащую цифру верной в строгом смысле, если абсолютная погрешность не превосходит половины единиц разряда, соответствующих этой цифре.
Если все значащие цифры верные, то говорят, что число записано со всеми верными цифрами.
Пример 1.3. При а* = 0,03045, Δ(а*)= 0,000003 число а* записано со всеми верными цифрами.
Иногда употребляется термин число верных цифр после запятой: подсчитывается число цифр после запятой от первой цифры до последней верной цифры. В последнем примере это число равно 5.
Довольно часто информация о некоторой величине задается пределами ее измерения:

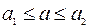 , (1.2)
, (1.2)
например, 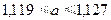 .
.
Принято записывать эти пределы с одинаковым числом знаков после запятой, Так как обычно достаточно грубого представления о погрешности, то в числах а1, а2 часто берут столько значащих десятичных цифр, сколько нужно, чтобы разность а1 — а2 содержала одну-две значащие цифр. Абсолютную или относительную погрешность обычно записывают в виде числа, содержащего одну или две значащих цифры. Информацию о том, что, а* является приближенным значением числа а с абсолютной погрешностью Δ (а*), иногда записывают в виде
а = а*± Δ(а*), (1.3)
числа а* и Δ(а*) принято записывать с одинаковым числом знаков после запятой. Например, записи
а = 1,132 ±0,004, а = 1,132 ±4*10-3
относятся к общепринятым и означают, что
1,132 - 0,004 < а < 1,132 + 0,004.
Соответственно информацию о том, что а* является приближенным значением числа а с относительной погрешностью (а*), записывают в виде
a = a*(1± δ(a*)). (1.4)
Например, записи
а = 1,132 (1 ± 0,004), а = 1,132(1 ± 4 *10-3), а = 1,132(1 ± 0,4℅)
означают, что
(1 - 0,004)1,132 < а < (1 + 0,004)1,132.
При переходе от одной из форм записи к другой надо следить, чтобы пределы измерения, указываемые новой формой записи, были шире старых, иначе такой переход будет незаконным. Например, при переходе от (1.2) к (1.3) должны выполняться неравенства
a*- Δ(a*) 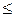 a1, a2
a1, a2 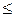 a* + Δ(a*),
a* + Δ(a*),
при переходе от (1.3) к (1.4) — неравенства
а*(1 - δ (а*)) 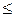 а* - Δ (а*), а* + Δ (а*)
а* - Δ (а*), а* + Δ (а*) 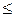 а*(1 + δ(а*)),
а*(1 + δ(а*)),
при переходе от (1,4) к (1.3) должны выполняться противоположные неравенства (пределы всегда расширяются!).
Следует различать принятую нами выше формально математическую и обиходную терминологии в рассуждении о величине погрешности. Если в постановке задачи говорится, что требуется найти решение с погрешностью 10-2, то чаще всего не имеется в виду обязательность этого требования. Предполагается лишь, что погрешность имеет такой порядок. Если, например, решение будет найдено с погрешностью 2-10-2, то такой результат, также удовлетворителен.
Вычислительная погрешность
Далее для краткости будем обозначать абсолютную погрешность числа x как Δx относительную погрешность как δХ .
1. Погрешность суммирования чисел х±Δх, у± Δy
Абсолютная: погрешность:
Δz = (x± Δx)+(y± Δy)=(x + y) ±(Δx± Δy)
Относительная погрешность:
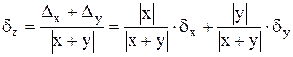
2. Погрешность вычитания чисел х±Δх, у± ΔY
Абсолютная: погрешность:
Δz = (x± Δx)-(y± Δy)=(x + y) ±(Δx± Δy)
Относительная погрешность:
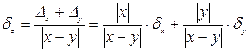
3. Погрешность умножения чисел х±Δх, у± Δy
Абсолютная: погрешность:
z = (x± Δx) (y± Δy)=xּy± yּΔx ±xּΔy± ΔxּΔy = xּy± yּΔx ±xּΔy
Относительная погрешность:
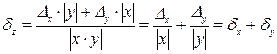
4. Погрешность деления чисел х±Δх, у± Δy
Абсолютная: погрешность:
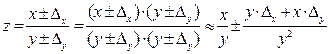
Относительная погрешность:
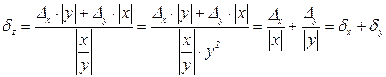
5. Погрешность функции, зависящей от одной переменной.
Абсолютная: погрешность:
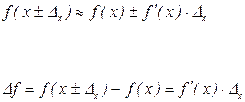
Относительная погрешность:
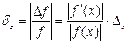 .
.
Отделение корней уравнения
Пусть дано уравнение, которое в общем виде записывается формулой
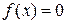 , (2.1)
, (2.1)
где f(x) любая действительная функция.
Точным корнем уравнения (2.1) на конечном или бесконечном отрезке [α,β] назовем всякое число ξ из промежутка, которое обращает функцию.f(x) в нуль. Так как уравнение может быть достаточно сложным, редко удается найти его точные корни. Задача состоит в том, чтобы найти приближенные корни и оценить, насколько точно это сделано.
Процесс нахождения приближенных корней уравнения общего вида f(x) = 0 проводится в два этапа:
1. Отделение корней, то есть установление возможно малых промежутков 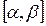 , в которых содержится один и только один корень уравнения (2.1);
, в которых содержится один и только один корень уравнения (2.1);
2. Уточнение приближенных корней.
Если ξ-точный корень, x приближенный корень уравнения (2.1), а ε точность, то для того, чтобы приближенный корень x был найден с заданной точностью ε достаточно потребовать выполнения неравенства: 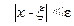 .
.
Теорема 2.1: Если непрерывная функция 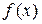 принимает значения противоположных знаков на концах
принимает значения противоположных знаков на концах 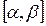 , т.е.
, т.е. 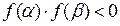 , то внутри этого отрезка содержится, по меньшей мере, один корень уравнения
, то внутри этого отрезка содержится, по меньшей мере, один корень уравнения 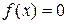 .
.
Корень 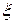 [
[ 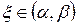 ] заведомо будет единственным, если производная
] заведомо будет единственным, если производная 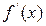 существует и сохраняет постоянный знак внутри интервала
существует и сохраняет постоянный знак внутри интервала 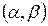 , т.е.
, т.е. 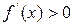 (или
(или 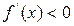 ) при
) при 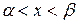 .
.
Метод половинного деления
Пусть уравнение (2.1) имеет на отрезке [a,b] один корень, а функция f(x) на данном отрезке непрерывна и f(a)·f(b)<0. Разделим отрезок [a,b] пополам точкой x1=(а+b)/2. Если f(x1)≠0 , то для продолжения вычислений выберем ту часть промежутка, где знаки функции различны. Концы полученного отрезка обозначим [a1,b1] и снова разделим отрезок [a1,b1] пополам точкой x2=( a1+ b1)/2 и т. д. В результате на каком-то этапе получим или точный корень уравнения(2.1) или бесконечную последовательность вложенных друг в друга отрезков [a1,b1], [a2,b2],… [an,bn],…таких, что
f(an)·f(bn)<0, (n=1,2,…) (2.2)
bn - an=2 -n·(b-a). (2.3)
Так как левые концы a1, a2,… ,an образуют монотонную неубывающую ограниченную последовательность, а правые концы b1 b2,…,bn образуют монотонную невозрастающую ограниченную последовательность, а расстояние между ними в силу (2.2) стремится к нулю, то у последовательностей существует общий предел . Число ξ, которое является общим пределом последовательностей {an} и {bn}, точный корень уравнения (2.1). Оценим погрешность решения на n-м шаге. Считаем до тех пор, пока длина промежутка не станет меньше заданной точности ε.
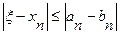
В качестве ответа возьмем середину отрезка [an,bn].
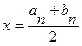 .
.
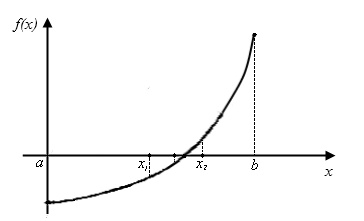
Рис.2.2. К объяснению метода половинного деления
Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, так как при увеличении точности значительно возрастает объём вычислений.
Пример 2.3. Найти, используя пакет Matchcad, методом половинного деления корень уравнения x4-x3-2x2+3x-3=0 на промежутке [1,2]
Функция koren(a,b,ε) возвращает длину отрезка, который будет меньше заданной точности ε, и значение корня на этом промежутке, если на концах отрезка [a,b] функция имеет противоположные знаки, или сообщение об отсутствии корня, в противном случае.
Метод легко реализуется на компьютере. Далее приводится листинг программы, написанной на языке, встроенном в систему Mathcad.
 Рис. 2.3. Листинг программы в Mathcad, реализующей метод половинного деления для примера 2.3
Рис. 2.3. Листинг программы в Mathcad, реализующей метод половинного деления для примера 2.3
Метод хорд
В этом методе нелинейная функция f(x) на отделенном промежутке
[a,b] заменяется хордой, проходящей через точки (a,f(a))и (b,f(b))
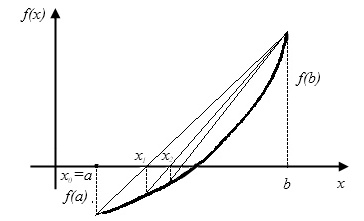
Рис.2.4. Метод хорд. Неподвижен правый конец промежутка b
Уравнение хорды: 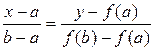 . Найдем точку пересечения хорды с горизонтальной осью. Полагая
. Найдем точку пересечения хорды с горизонтальной осью. Полагая 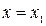 и
и 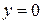 , получим
, получим
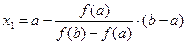 .
.
Точку x1 принимаем за новую границу отрезка, где содержится корень. Через эту точку с координатами (x1,f(x1)) и соответствующую границу предыдущего интервала (b,f(b)) опять проводим хорду, находим 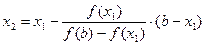 и т.д., получая последовательность x1,x2,x3,…xn,…, сходящуюся к корню уравнения.
и т.д., получая последовательность x1,x2,x3,…xn,…, сходящуюся к корню уравнения.
Вторая производная 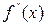 сохраняет постоянный знак на
сохраняет постоянный знак на 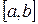 . Следовательно, возможны два случая. Если f(b)·f "(b)>0, то хорда имеет правый фиксированный конец, причем последовательность x0,x1,…xn приближается к корню слева. За начальное приближение x0, естественно, берут a
. Следовательно, возможны два случая. Если f(b)·f "(b)>0, то хорда имеет правый фиксированный конец, причем последовательность x0,x1,…xn приближается к корню слева. За начальное приближение x0, естественно, берут a
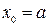 ;
; 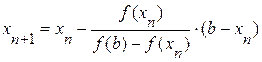 ;
; 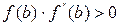 ;
;
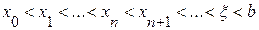 .
.
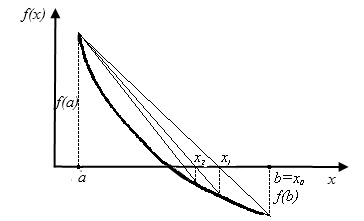
Рис.2.5. Метод хорд. Неподвижен левый конец промежутка a
Если f(a)·f "(a)>0, то хорда имеет левый фиксированный конец, причем последовательность x0,x1,…xn … приближается к корню справа. За начальное приближение x0, берут b
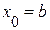 ;
; 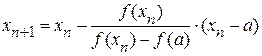 ;
; 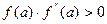 ;
;
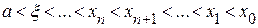 .
.
Для оценки точности можно воспользоваться формулой
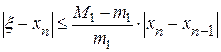 ,
,
где 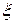 -точный корень,
-точный корень, 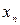 - приближенный корень,
- приближенный корень, 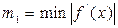 ,
, 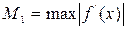 на промежутке [a,b]. Считаем до тех пор пока, не выполнится условие
на промежутке [a,b]. Считаем до тех пор пока, не выполнится условие 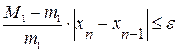 . Если имеет место неравенство
. Если имеет место неравенство 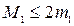 , то счет можно прекратить, когда.
, то счет можно прекратить, когда. 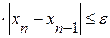
Пример 2.4. Найти методом хорд корень уравнения x4-x-1=0
Решение находим, используя пакет Mathcad.
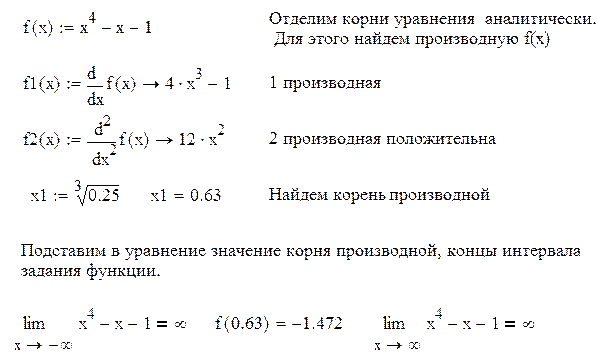
Функция монотонна на промежутках (-∞, 0.63), (0.63, ∞) и меняет на концах промежутков знак. Уравнение имеет два корня. Сузим промежутки отделения корней методом проб, т.е. подстановкой.
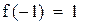 |
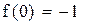 |
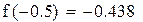 |
Первый корень принадлежит промежутку (-1,-0.5)
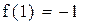 |
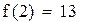 |
Второй корень принадлежит промежутку (1,1.5)
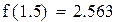 |
Будем находить корень на промежутке (-1,-0.5)
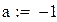 |
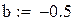 |
Вторая производная всюду положительна, функция положительна в точке a = -1, значит, этот конец неподвижен.
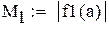 |
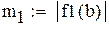 |
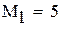 |
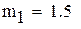 |
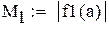 |
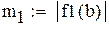 |
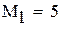 |
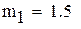 |
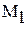 -максимальное, a -максимальное, a 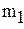 -минимальное значение модуля производной на промежутке -минимальное значение модуля производной на промежутке |
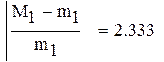 |
так как 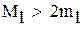 , множитель
, множитель 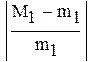
нужно учитывать при оценке точности решения,
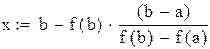 |
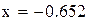 |
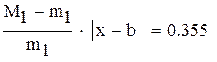 |
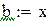 |
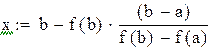 |
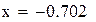 |
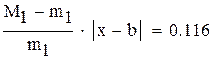 |
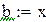 |
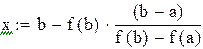 |
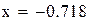 |
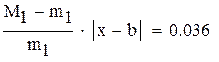 |
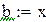 |
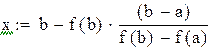 |
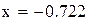 |
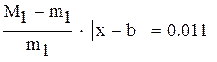 |
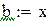 |
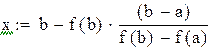 |
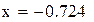 |
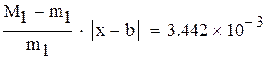 |
Нашли корень исходного уравнения 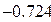 с точностью
с точностью 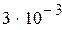 .
.
Рис. 2.6. Вычисления в Mathcad, реализующие метод хорд для примера 2.4
Метод секущих
Заменим производную функции f(x) в точке xn на функцию F(x) в этой же точке. Подставим ее вместо производной в формулу Ньютона.
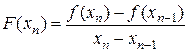 ,
,
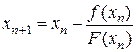 .
.
В методе секущих требуются задать для начала счета два значения x0 и x1. Отрезок [x0, x1] не обязательно должен содержать корень уравнения.
Оценка точности делается, как в обыкновенном методе Ньютона
Метод итераций
Пусть дано уравнение
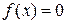 , (2.1)
, (2.1)
где 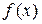 - непрерывная функция. Заменим его равносильным уравнением
- непрерывная функция. Заменим его равносильным уравнением
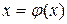 . (2.2)
. (2.2)
Выберем каким-либо способом приближенное значение корня 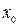 и подставим его в правую часть уравнения (2). Получим некоторое число
и подставим его в правую часть уравнения (2). Получим некоторое число 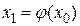 . Повторим данную процедуру с x1, получим
. Повторим данную процедуру с x1, получим 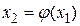 . Повторяя описанную процедуру, будем иметь последовательность чисел:
. Повторяя описанную процедуру, будем иметь последовательность чисел:
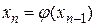 , где n=1,2,…. (2.3)
, где n=1,2,…. (2.3)
Пусть у этой последовательности существует предел 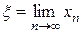 . Перейдем к пределу в равенстве (2.3). Предполагая функцию φ(х) непрерывной, найдем:
. Перейдем к пределу в равенстве (2.3). Предполагая функцию φ(х) непрерывной, найдем: 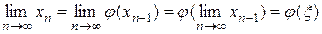 или
или 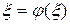 .
.
Таким образом, предел является корнем уравнения 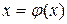 и может быть вычислен по формуле (2.3) с любой степенью точности.
и может быть вычислен по формуле (2.3) с любой степенью точности.
На рисунке дана геометрическая интерпретация метода итераций в зависимости от знака производной функции φ(х).
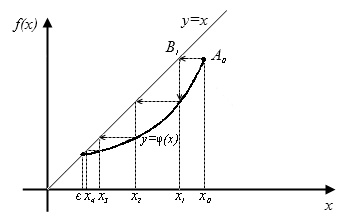
Рис 2.10 φ'(х) > 0.
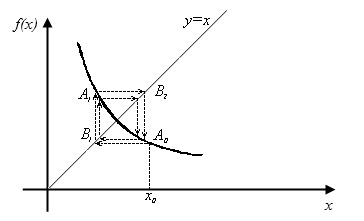
Рис.2.11 φ'(х) < 0
Достаточное условие сходимости процесса итераций определяется в следующей теореме.
Теорема 2.3: Пусть функция 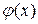 определена и дифференцируема на отрезке
определена и дифференцируема на отрезке 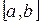 , причем все ее значения
, причем все ее значения 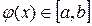 . Тогда, если существует правильная дробь q такая, что
. Тогда, если существует правильная дробь q такая, что 
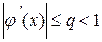 при
при 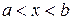 , то
, то
1. процесс итерации 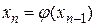 (n=1,2,..) сходится независимо от начального значения
(n=1,2,..) сходится независимо от начального значения 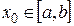 ;
;
2. предельное значение 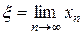 является единственным корнем уравнения
является единственным корнем уравнения 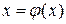 на отрезке
на отрезке 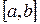 при
при 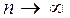 .
.
Для оценки погрешности приближения xn получается формула:
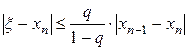 ,
,
где 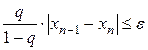 ; а
; а 
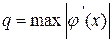 на [a,b] При заданной точности ответа ε итерационный процесс прекращается, если
на [a,b] При заданной точности ответа ε итерационный процесс прекращается, если
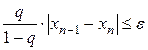 . Если q<|0.5|
. Если q<|0.5|  , то
, то 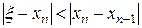 .
.
Сходимость итерационной последовательности определяется видом функции φ(х). Преобразование к виду (2.2) можно провести различными способами. Чтобы обеспечить сходимость, можно искать решение в виде
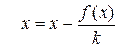 , (2.4)
, (2.4)
где k-целое число. Уравнение (2.4) это уравнение (2.1) с 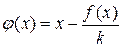 . Оно равносильно исходному уравнению (2.1). Для сходимости метода итераций по теореме 2.3 необходимо, чтобы
. Оно равносильно исходному уравнению (2.1). Для сходимости метода итераций по теореме 2.3 необходимо, чтобы 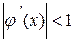 . Дифференцируем φ(х) и получаем
. Дифференцируем φ(х) и получаем 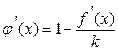 . Решаем неравенство
. Решаем неравенство 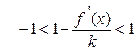 :
:
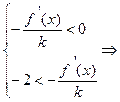
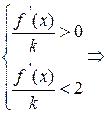
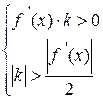 .
.
Чтобы условие сходимости выполнялось на всем промежутке [a,b], нужно взять 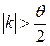 , где
, где 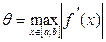 .
.
Итак, если выполняются условия 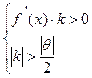 то метод итераций сходится для уравнения
то метод итераций сходится для уравнения 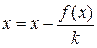
Пример 2.6. Методом итераций найти корень уравнения
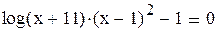
на промежутке (-10,-9,6) с четырьмя знаками после запятой.
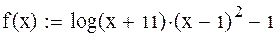
| Находим производную f(x) |
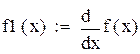
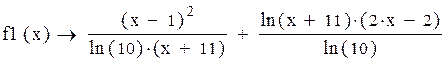
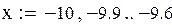

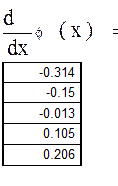
По значению производной f(x) выбираем положительное k
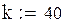
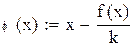
В качестве начального приближения выберем левый конец промежутка. Сделаем шесть итераций.
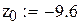
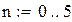
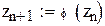
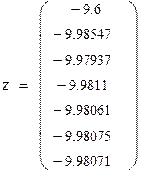
Так как значения производной φ(x) по модулю меньше 0.5, то оцениваем точность вычислений по формуле 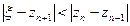
 |
Корень уравнения x = -9.98071 найден с точностью 0.000038
Рис. 2.12. Вычисления в Mathcad, реализующие метод итераций для примера 2.6
Метод итераций
Дана система, состоящая из n линейных уравнений с n неизвестными:
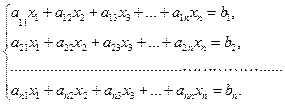 (3.1)
(3.1)
Обозначим через 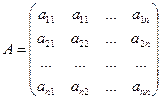 -матрицу коэффициентов системы (3.1), через
-матрицу коэффициентов системы (3.1), через 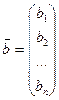 - столбец свободных членов и через
- столбец свободных членов и через 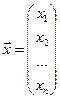 - столбец неизвестных.
- столбец неизвестных.
Тогда систему (3.1) можно записать в виде матричного уравнения
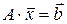 .
.
Решением системы будут числа x1, x2, …, xn. Определитель системы не равен нулю. Предполагая, что диагональные коэффициенты 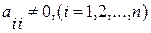 разрешим первое уравнение системы относительно x1, второе – относительно x2 и т.д. Тогда получим равносильную систему, которая называется приведенной к виду , удобному для итераций.
разрешим первое уравнение системы относительно x1, второе – относительно x2 и т.д. Тогда получим равносильную систему, которая называется приведенной к виду , удобному для итераций.
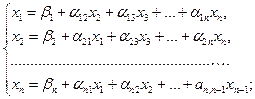 , (3.2)
, (3.2)
где 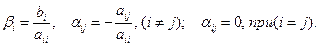 (3.3)
(3.3)
Введем в рассмотрение матрицы:
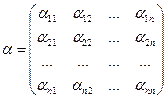 и
и 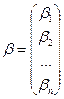 .
.
Тогда систему можем записать в матричном виде:
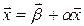 . (3.2')
. (3.2')
Заметим, что систему (3.1) можно приводить к виду (3.2) любыми линейными преобразованиями. Систему (3.2) будем решать методом последовательных приближений, используя матричную запись. За нулевое приближение принимаем, например, столбец свободных членов: 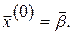 Далее последовательно строим матрицы-столбцы:
Далее последовательно строим матрицы-столбцы: 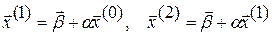 и т.д.
и т.д.
Любое (k+1)-ое приближение вычисляют по формуле:
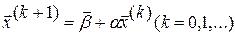 . (3.4)
. (3.4)
Если последовательность приближений 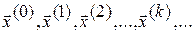 имеет предел
имеет предел 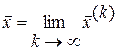 , то этот предел является решением системы (3.2). В самом деле, переходя к пределу в равенстве (3.4), будем иметь:
, то этот предел является решением системы (3.2). В самом деле, переходя к пределу в равенстве (3.4), будем иметь: 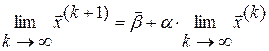 или
или 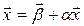 т.е. предельный вектор
т.е. предельный вектор 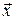 является решением системы.
является решением системы.
Напишем формулы приближений в развернутом виде:

Метод итераций – метод последовательных приближений. Процесс итерации хорошо сходится, т.е. число приближений, необходимых для получения корней системы с заданной точностью, невелико, если элементы матрицы a малы по абсолютной величине. Иными словами, для успешного применения процесса итерации модули диагональных коэффициентов системы должны быть велики по отношению к модулям недиагональных коэффициентов этой системы. Свободные члены при этом роли не играют.
Выясним, при каких достаточных условиях последовательность приближений 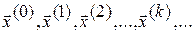 имеет предел.
имеет предел.
Теорема 3.1
Если для приведенной системы выполнено, по меньшей мере, одно из условий:
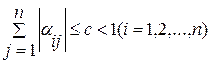 или
или 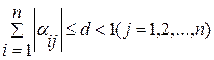 ,
,
то процесс итерации сходится к единственному решению этой системы, независимо от выбора начального приближения.
В теореме (3.1) - «с» это значение максимальной суммы модулей элементов в строках, а «d» в столбцах матрицы α. Эти числа называют нормой матрицы α по строкам и по столбцам соответственно.
Следствие из теоремы (3.1).
Для приведенной системы 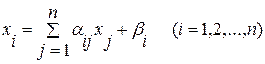
полученной из системы 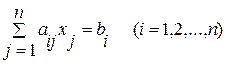 по формулам (3.3)
по формулам (3.3)
 метод итераций сходится, если выполнены неравенства
метод итераций сходится, если выполнены неравенства
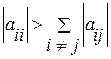 (i=1,2,…n),
(i=1,2,…n),
т.е. модули диагональных коэффициентов системы больше суммы модулей всех остальных коэффициентов.
Метод Зейделя
Метод Зейделя является модификацией метода итерации. Он заключается в том, что при вычислении (k+1)-го приближения неизвестного 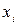 при i>1 используют уже вычисленные ранее (k+1)-е приближения неизвестных
при i>1 используют уже вычисленные ранее (k+1)-е приближения неизвестных 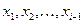
Пусть дана приведенная линейная система 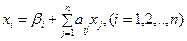
Выберем произвольно начальные приближения корней 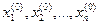 ,
,
Далее, предполагая, что k-е приближения 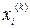 корней известны, согласно Зейделю будем строить (k+1)-е приближения корней по следующим формулам:
корней известны, согласно Зейделю будем строить (k+1)-е приближения корней по следующим формулам:
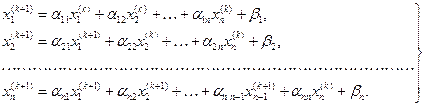
Процесс повторяется до тех пор, пока разница между двумя соседними приближениями не будет меньше необходимой точности.
Условия сходимости те же, что и для метода итераций.
Пример 3.2. Пусть дана линейная система и приближенные корни системы:
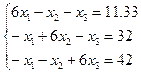 и
и 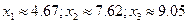 .
.
Приведем систему к виду, удобному для итераций
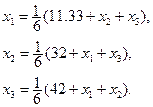
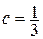 поэтому метод сходится
поэтому метод сходится
Взяв в качестве начальных приближений: 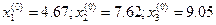 , получим:
, получим:
при k=1 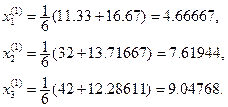
при k = 2 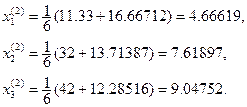
Найдем разность по модулю между соседними приближениями:
|  -
- 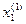 | = 0,00048
| = 0,00048
| 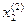 -
- 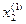 | = 0,00047
| = 0,00047
| 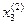 -
- 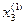 | = 0,00016
| = 0,00016
Так как для приведенной системы выполняется условие сходимости при 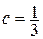 ,то полученное приближение имеет погрешность, не превышающую 0,0005.
,то полученное приближение имеет погрешность, не превышающую 0,0005.
Таким образом, в качестве решения можем принять 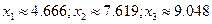 .
.
Метод релаксаций
Пусть дана система: (3.1)
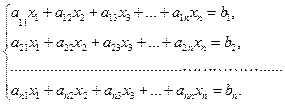
Преобразуем эту систему следующим образом: перенесем свободные члены налево и разделим первое уравнение на 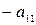 , второе – на
, второе – на 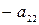 и т.д. Тогда получим систему, приготовленную к релаксации:
и т.д. Тогда получим систему, приготовленную к релаксации: 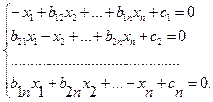 , где
, где 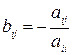
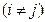 и
и 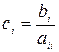 .
.
Пусть 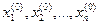 - начальное приближение решения системы. Подставляя эти значения в систему, получим в правых частях уравнений системы некоторые числовые значения . Будем называть их невязками. Невязки обращаются в нуль при подстановке корней в уравнения системы
- начальное приближение решения системы. Подставляя эти значения в систему, получим в правых частях уравнений системы некоторые числовые значения . Будем называть их невязками. Невязки обращаются в нуль при подстановке корней в уравнения системы
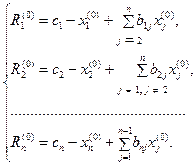 .
.
Если одной из неизвестных 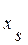 дать приращение
дать приращение 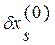 , то соответствующая невязка
, то соответствующая невязка 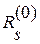 уменьшится на величину
уменьшится на величину 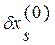 , а все остальные невязки
, а все остальные невязки 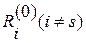 увеличатся на величину
увеличатся на величину 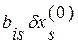 . Таким образом, чтобы обратить очередную невязку
. Таким образом, чтобы обратить очередную невязку 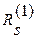 в нуль, достаточно величине
в нуль, достаточно величине 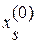 дать приращение
дать приращение 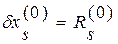 и мы будем иметь
и мы будем иметь 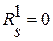 и
и 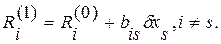
Суть метода заключается в том, чтобы на каждом шаге обращать в нуль максимальную по модулю невязку, изменяя значения соответствующей компоненты приближения. Процесс заканчивается, когда все невязки преобразованной системы будут равны нулю с заданной степенью точности.
Пример3.1: Пусть дана линейная система. Решить с точностью 0.01.
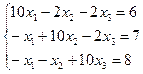 .
.
Приведем систему к виду, удобному для релаксации:
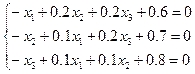 .
.
Выбирая в качестве начальных приближений корней нулевые значения 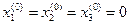 , находим
, находим 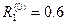 ,
, 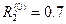 ,
, 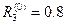 .
.
Согласно общей теории полагаем: 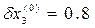 . Отсюда получаем невязки
. Отсюда получаем невязки
