Лабораторная работа 11. Вычисление функций. Построение графиков
Варианты заданий:
1. Рассчитайте значение функции, заданной в варианте с использованием элементарных функций в командном окне при заданном значении переменной.
| Вариант | Функция | Значения переменных |
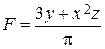 | 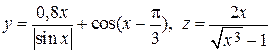 ,x= –5 ,x= –5 | |
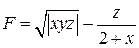 | 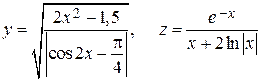 , x = 10. , x = 10. | |
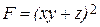 | 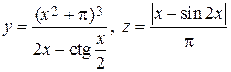 , x = 3 , x = 3 | |
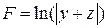 | 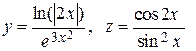 , x = –1 , x = –1 | |
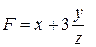 | 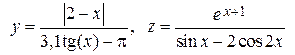 , x = 4 , x = 4 | |
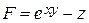 | 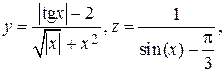 x = –8 x = –8 | |
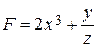 | 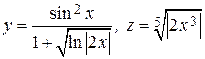 , x = 0 , x = 0 | |
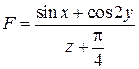 | 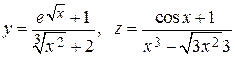 , x = –9 , x = –9 | |
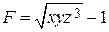 | 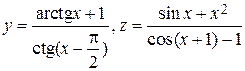 , x = 7 , x = 7 | |
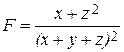 | 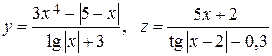 , x1 = –6 , x1 = –6 |
2. Построить графики функций y=f(x) на заданном интервале (от a до b), рассчитав значения с заданным шагом (h), для каждого графика вывести легенду, название графика, подписи осей. Графики построить в двух вариантах: 1 – в одном графическом окне на одном поле; 2 – в одном графическом окне в двух полях.
Таблица 2 Варианты задания для построения графиков
| № | Функция 1 | Функция 2 | a | b | h |
| у = sin(x) | z = exp(x+3)/5000 –1 | –2π | 2π | π /20 | |
| у = cos(x) | z = 0,00025x3-x-0,6 | –2p | 2π | π /20 | |
| у = |tg(x)| + 0,1 | z = (1+x)2 | –2π | 2π | π /20 | |
| у = (х2-1)/15 | z = 1+sin(x) | –2π | 2π | π /20 | |
| у = (хЗ–2)/15 | z = 5cos(x) | –2π | 2π | π /20 | |
| у = х2–10 | z = 0,025exp(-1,2x) | –5 | 1/10 | ||
| у = 3sin(x) | z = 0,015x3 | –5 | 1/10 | ||
| у = 4sin(x) | z = 0,05x2 | 1/5 | |||
| у = 6sin(x) | z = 0,01x3 | –10 | 1/5 | ||
| у = 2+cos(x) | z = -0,05(x2 + 10cos(x)) | –8 | 1/5 | ||
| у = sin2(x/3) | z = 0,01(x2-40sin(x)) | –8 | 1/10 | ||
| у = cos3(x) | z = sin(x) + sin(2x) | –π | π | π /8 | |
| у = 0,5х + cos2(x) | z = sin2(x) + cos(x) | –π | π | π /8 | |
| у = sin(x) + cos2(2x) | z = x(0,5 + x)exp(0,1x) | –π | π /8 | ||
| у = |sin(x)|exp(x/2) | z = 5x – x2+sin(x) | 0,5 |
Лабораторная работа 12. Программирование. Использование функций. Решение дифференциальных уравнений.
Таблица 1. Варианты заданий
| № | Система ОДУ | Начальные условия | |
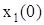 | 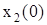 | ||
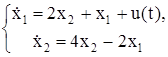 | 1.5 | 1.5 | |
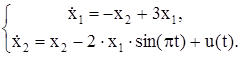 | -1 | ||
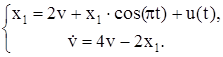 | 1.5 | 1.5 | |
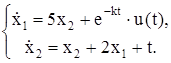 | 1.5 | ||
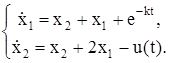 | 0.5 | 1.5 | |
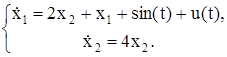 | 0.5 | ||
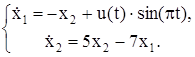 | |||
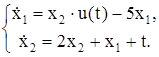 | 1.5 | ||
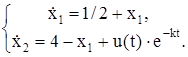 | |||
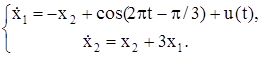 | -1 | ||
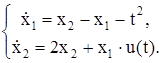 | 1.5 | 1.5 | |
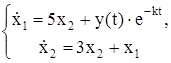 | -1 | 1.5 | |
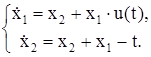 | 0.5 | ||
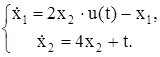 | -2 | ||
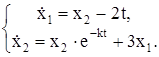 |
Лабораторная работа 13. Исследование систем управления в Scilab. Описание САУ, исследование переходных и частотных характеристик САУ.
В процессе выполнения практической работы студент (курсант) обязан:
– Выбрать дифференциальное уравнение системы из табл. 5 согласно варианту задания и вывести передаточную функцию системы.
– Выбрать задание к лабораторной работе в соответствии с вариантом задания из табл. 6.
– В теоретической части работы для указанных вариантов в задании звеньев по передаточной функции, используя преобразование Лапласа, вывести выражения для переходных и импульсных характеристик. Теоретически рассчитать импульсные и переходные характеристики указанных в задании переходных функций при заданных в задании параметрах и заданном временном интервале.
– В практической части работы собрать схемы для моделирования переходных и импульсных характеристик в среде визуального моделирования (Simulink или Xcos). Промоделировать ТДЗ и получить переходные характеристики при указанных в задании параметрах передаточных функций. Поместить полученные переходные характеристики в отчет по работе. Используя скриптовый язык, записать модули для создания указанных в задании передаточных функций. С помощью соответствующих функций получить переходные и импульсные характеристики для указанных в задании параметрах передаточных функций, поместить их в отчет по работе. Используя переходные временные характеристики, рассчитать показатели качества работы системы.
– Проанализировать полученные результаты. Сделать вывод о влиянии параметров ТДЗ на переходные и импульсные характеристики.
Таблица 6
Варианты заданий
| № в-та | Название звена | Значения параметров |
| Усилительное Интегрирующее | k = 1; 2; 5 | |
| Апрериодическое 1-го порядка Изодромное Интегрирующее с замедлением | 1) k = 1= const, T = 0,1; 0,5; 1 2) T = 0,5 =const, k = 0,5; 1; 5 | |
| Колебательное | 1) k = 1=const, T = 0.1= const, 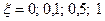 2) 2)  =const, k = 1=const, T = 0,1; 0,5; 1 3) =const, k = 1=const, T = 0,1; 0,5; 1 3) 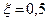 =const, T = 0,5 = const, k = 0,5; 1; 5 =const, T = 0,5 = const, k = 0,5; 1; 5 | |
| Усилительное, Интегрирующее | k = 0,5; 1; 2 | |
| Апериодическое 1-го порядка, Консервативное, Дифференцирующее с замедлением | 1) k = 2 =const, T = 0,1; 0,5; 1 2) T = 0,75=const, k = 0,5; 1; 5 |
Продолжение табл. 6
| № в-та | Название звена | Значения параметров |
| Колебательное | 1) k = 1=const, T = 0,25 = const, 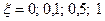 2) 2) 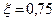 =const, k = 1= const, T = 0,1; 0,5; 1 3) =const, k = 1= const, T = 0,1; 0,5; 1 3) 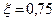 = const, T = 0.5=const, k = 0.5; 1; 5 = const, T = 0.5=const, k = 0.5; 1; 5 | |
| Усилительное Интегрирующее | k = 0,1; 0,2; 0,5 | |
| Апериодическое 1-го порядка Консервативное Дифференцирующее с замедлением | 1) k = 1= const, T = 0,1; 0,5; 0,75 2) T = 0,75 = const, k = 0,5; 1; 5 | |
| Колебательное | 1) k = 1=const, T = 0,1 = const, 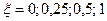 2) 2)  = const, k = 1 = const, T = 0,1; 0,5; 0,75 3) = const, k = 1 = const, T = 0,1; 0,5; 0,75 3)  = const, T = 0,5 = const, k = 0,5; 1; 5 = const, T = 0,5 = const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 0,5; 1; 2 | |
| Апериодическое 1-го порядка Консервативное Дифференцирующее с замедлением | 1) k = 1=const, T = 0,1; 0,5; 1 2) T = 0,5 =const, k = 0,5; 1; 2 | |
| Колебательное | 1) k = 0,75 = const, T = 0,25 = = const, 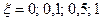 2) 2)  = const, k = 2 = const, T= 0,1; 0,5; 1 3) = const, k = 2 = const, T= 0,1; 0,5; 1 3)  = const, T = 0,75 = const, k = 0,5; 1; 5 = const, T = 0,75 = const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 1; 2; 5 | |
| Апериодическое 1-го порядка Изодромное Интегрирующее с замедлением, | 1) k = 1= const, T = 0,1; 0,5; 1 2) T = 0,5 =const, k = 0.5; 1; 5 | |
| Колебательное | 1) k = 1=const, T = 0,25 = const, 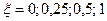 2) 2) 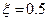 = const, k = 1 = const, T= 0,1; 0,5; 1 3) = const, k = 1 = const, T= 0,1; 0,5; 1 3)  = const, T = 0,5 = const, k = 0,5; 1; 2 = const, T = 0,5 = const, k = 0,5; 1; 2 |
Продолжение табл. 6
| № в-та | Название звена | Значения параметров |
| Усилительное Интегрирующее | k = 0,1; 0,2; 0,5 | |
| Апериодическое 1-го порядка Форсирующее 1-го порядка Изодромное | 1) k = 1=const, T = 0,1; 0,5; 1 2) T = 0,5 =const, k = 0,5; 1; 5 | |
| Колебательное Форсирующее 2-го порядка | 1) k = 1= const, T = 0,1= const, 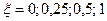 2) 2) 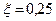 = const, k = 1 = const, T = 0,1; 0,5; 1 3) = const, k = 1 = const, T = 0,1; 0,5; 1 3) 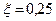 = const, T= 0,5 = const, k = 0,5; 1; 5 = const, T= 0,5 = const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 0,1; 0,25; 0.5 | |
| Апериодическое 1-го порядка Консервативное Дифференцирующее с замедлением | 1) k = 2=const, T = 0,1; 0,5; 1 2) T = 1=const, k = 0,5; 1; 2 | |
| Колебательное | 1) k = 1=const, T = 0,1=const, 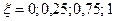 2) 2)  =const, k = 1=const, T = 0,1; 0,5; 0,75 3) =const, k = 1=const, T = 0,1; 0,5; 0,75 3)  =const, T = 0,5=const, k = 0,5; 1; 2 =const, T = 0,5=const, k = 0,5; 1; 2 | |
| Усилительное Интегрирующее Дифференцирующее | k = 0,25; 0,5; 1 | |
| Апериодическое 1-го порядка Дифференцирующее с замедлением | 1) k = 1=const, T = 0,1=const; 0,5; 0,75; 1 2) T = 0,5=const, k = 0,5; 1; 5 | |
| Колебательное | 1) k = 1=const, T = 0,5=const, 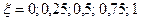 2) 2) 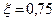 =const, k = 1=const, T = 0,1; 0,5; 1 3) =const, k = 1=const, T = 0,1; 0,5; 1 3) 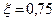 =const, T = 0,5 = const, k = 0,5; 1; 5 =const, T = 0,5 = const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 1; 1,5; 2 |
Продолжение табл. 6
| № в-та | Название звена | Значения параметров |
| Апериодическое 1-го порядка Консервативное Дифференцирующее с замедлением | 1) k = 0,75 = const, T= 0,1; 0,5; 1 2) T = 0,75 =const, k = 0,5; 1; 5 | |
| Колебательное | 1) k = 1= const, T = 0,25, 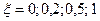 2) 2) 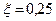 = const, k = 1= const, T = 0,1; 0,5; 1 3) = const, k = 1= const, T = 0,1; 0,5; 1 3) 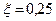 = const, T = 0,5, k = 0,5; 1; 5 = const, T = 0,5, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 0,25; 0,5; 1 | |
| Апериодическое 1-го порядка Консервативное Изодромное | 1) k = 1= const, T = 0,1; 0,5; 0,75; 1 2) T = 0,5=const, k = 0,5; 1; 2; 5 | |
| Колебательное | 1) k = 1,5= const, T = 0,25 = const, 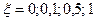 2) 2) 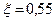 = const, k = 1= const, T = 0,1; 0,5; 1 3) = const, k = 1= const, T = 0,1; 0,5; 1 3) 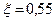 = const, T = 0,5 = const, k = 0,5; 1; 5 = const, T = 0,5 = const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 1; 2; 5 | |
| Апериодическое 1-го порядка Изодромное Дифференцирующее с замедлением | 1) k = 1= const, T = 0,1; 0,5; 1 2) T = 0,5= const, k = 0,5; 1; 5 | |
| Колебательное | 1) k = 1= const, T = 0,25 = const, 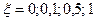 2) 2)  = const, k = 1= const, T = 0,25; 0,5; 1 3) = const, k = 1= const, T = 0,25; 0,5; 1 3)  =const, T = 0,75 = const, k = 0,5; 1; 5 =const, T = 0,75 = const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 0,1; 0,25; 0,5 | |
| Апериодическое 1-го порядка Консервативное Форсирующее 1-го порядка | 1) k = 1= const, T = 0,1; 0,5; 1 2) T = 0,5 = const, k = 0,5; 1; 5 |
Окончание табл. 6
| № в-та | Название звена | Значения параметров |
| Колебательное | 1) k = 1,5 = const, T = 0,1=const, 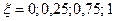 2) 2)  =const, k = 1,5 = const, T = 0,1; 0,5; 0,75 3) =const, k = 1,5 = const, T = 0,1; 0,5; 0,75 3)  =const, T = 0,25 = const, k = 0,5; 1; 2 =const, T = 0,25 = const, k = 0,5; 1; 2 | |
| Усилительное Интегрирующее | k = 0,5; 1; 2 | |
| Апериодическое 1-го порядка Консервативное Дифференцирующее с замедлением | 1) k = 1,25 = const, T = 0,25; 0,5; 1 2) T = 0,75 = const, k = 0,5; 1; 2 | |
| Колебательное | 1) k = 1= const, T = 0,25= const, 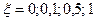 2) 2) 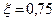 = const, k = 1, T = 0,1; 0,5; 1 3) = const, k = 1, T = 0,1; 0,5; 1 3) 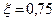 = const, T = 0,5= const, k = 0,5; 1; 5 = const, T = 0,5= const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 0,25; 0,75; 1 | |
| Апериодическое 1-го порядка Консервативное Форсирующее 1-го порядка Дифференцирующее с замедлением | 1) k = 1,5 = const, T = 0,1; 0,5; 1 2) T = 0,55 = const, k = 0,5; 1; 2 | |
| Колебательное | 1) k = 1= const, T = 0,25= const, 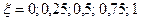 2) 2) 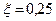 = const, k = 1= const, T = 0,1; 0,5; 1 3) = const, k = 1= const, T = 0,1; 0,5; 1 3) 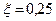 = const, T = 0,5= const, k = 0,5; 1; 2 = const, T = 0,5= const, k = 0,5; 1; 2 |
