Использование MatLab для моделирования систем

На основе передаточных функций

Использование команд языка сценариев

В среде MatLab существует несколько возможностей задания передаточных функций линейных систем управления. В случае работы с помощью командной строки либо файла сценария наиболее рационально использовать функцию tf (transfer function).

Синтаксис функции ft:

f = tf (num, den), где num – коэффициенты полинома числителя передаточной функции, идущие по убыванию степени s, а den – коэффициенты полинома знаменателя передаточной функции, идущие по убыванию степени s.

Например, передаточная функция

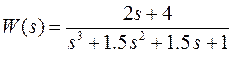(17)

вводится следующим образом:

>> n = [2 4]

n =

2 4

>> d = [1 1.5 1.5 1]

d =

1.0000 1.5000 1.5000 1.0000

>> f = tf ( n, d )

Transfer function:

2 s + 4

-------------------------

s^3 + 1.5 s^2 + 1.5 s + 1

Еще один способ задания передаточной функции (17):

>> f = tf ( [2 4], [1 1.5 1.5 1] );

Функции для получения временных характеристик на основе передаточных функций приведены в табл. 4.

Таблица 4

Функции для представления временных характеристик

Функция	Описание функции
step(f) step(f, t)	Вывод в виде графика переходной характеристики системы
impulse(f) impulse(f, t)	Вывод в виде графика импульсной характеристики системы
Примечание. f – передаточная функция; t – интервал времени, для которого будет рассчитан переходный процесс

Использование Simulink

Еще одним способом задания систем в виде передаточных функций является использование пакета Simulink, входящего в состав MatLab.

Для представления передаточной функции в Simulink используется блок Transfer Fcn. Блок передаточной характеристики Transfer Fcn задает передаточную функцию в виде отношения полиномов

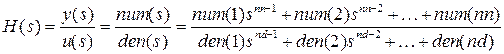, (18)

где nn и nd – порядок числителя и знаменателя передаточной функции, порядок числителя не должен превышать порядок знаменателя, num – вектор или матрица коэффициентов числителя, den – вектор коэффициентов знаменателя. Параметры блока Transfer Fcn:

– Numerator – вектор или матрица коэффициентов полинома числителя.

– Denominator – вектор коэффициентов полинома знаменателя.

– Absolute tolerance – абсолютная погрешность.

Исследование переходных характеристик осуществляется путем подачи на вход блока, представляющего передаточную функцию (блок Transfer Fcn), единичного ступенчатого сигнала (блоки Constant или Step). Входной сигнал блока должен быть скалярным. Чтобы получить переходный процесс, необходимо поместить на схему блок Scope и соединить его вход с выходом блока, переходный процесс которого необходимо получить. На рис. 6. показан пример моделирования колебательного звена с помощью блока Transfer Fcn (схема в Simulink и переходные процессы, полученные в блоке Scope). Начальные условия при использовании блока Transfer Fcn полагаются нулевыми.

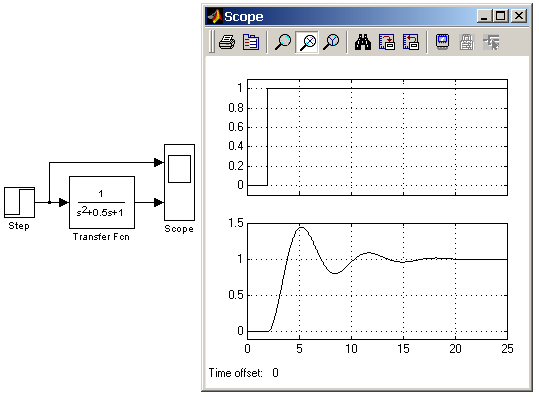
Рис. 6. Пример моделирования колебательного звена с помощью Simulink

Использование SciLab для моделирования систем на основе передаточных функций

Использование script-языка

При использовании script-языка SciLab для представления линейных систем используется функция syslin.

Синтаксис:

sl = syslin(dom, N, D)

sl = syslin(dom, H)

Параметры функции syslin:

dom – символьная переменная, которая может принимать два значения: 'c' или 'd'. dom определяет временной домен системы и может принимать следующие значения: dom='c' для систем непрерывных во времени; dom='d' для дискретно-временных систем;

N, D – полиномиальные матрицы;

H – рациональная матрица;

Выражение s = poly(0,'s') задаёт полином, соответствующий оператору Лапласа; переменная s может быть использована в дальнейшем. Наряду с таким заданием можно использовать и константу %s.

Далее приведены альтернативные способы задания двух ПФ 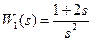и .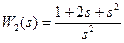

Пример 1:

s = poly(0, 's');

H1 =(1+2*s)/s^2

W1 = syslin('c', H1)

H2 = (1+2*s+s^2)/s^2

W2 = syslin('c', H2)

Пример 2:

s = poly(0, 's');

W1 = syslin('c', 1+2*s, s^2)

W2 = syslin('c', 1+2*s+s^2, s^2)

Пример 3:

W1 = syslin('c', 1+2*%s, %s^2)

W2 = syslin('c', 1+2*%s+%s^2, %s^2)

Для исследования временных характеристик используется функция csim, предназначенная для моделирования линейной системы

[y [,x]] = csim(u, t, sl),

где u – функция управления, принимает значения ‘step’ или ‘impulse’ в зависимости от вызываемой временной характеристики;

t – действительный вектор, характеризующий время; t(1) – начальное время x0=x(t(1));

sl – передаточная функция, представленная функцией syslin.

Далее рассмотрим в качестве примера моделирование апериодических звеньев первого порядка с различными значениями постоянных времени. Результат моделирования в виде переходных характеристик приведен на рис. 7.

Пример:

// построение переходных характеристик

// апериодического звена 1-го порядка

K = 1; // коэффициент усиления

T1 = 0.1; // постоянные времени

T2 = 0.5;

T3 = 1;

W1 = syslin('c', K/(T1*%s + 1));// задать ПФ

W2 = syslin('c', K/(T2*%s + 1));

W3 = syslin('c', K/(T3*%s + 1));

t = 0:0.05:5; // временной интервал

h1 = csim('step', t, W1); // моделирование подачи

h2 = csim('step', t, W2); // на вход ПФ

h3 = csim('step', t, W3); // ступенчатого воздействия

// построение графиков

plot(t, h1, 'r', t, h2, 'g', t, h3, 'b');

xgrid(2); // установка сетки на графике

// установка подписей графика и осей

xtitle('h(t)', 'time, c', 'h(t)');

legend('T=0.1', 'T=0.5', 'T=1'); // подпись легенды

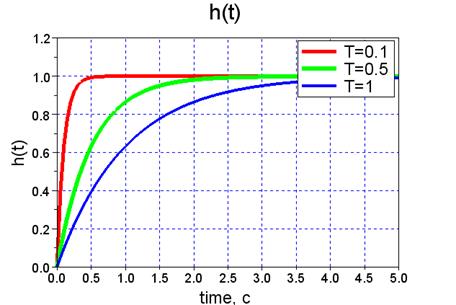
Рис. 7. Переходные характеристики апериодических звеньев в SciLab

Рекомендации по моделированию дифференцирующего