Подставив цифровые значения k R g в (10.1) получим формулу для скорости звука в воздухе

а = 20 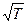(10.2.)

Следовательно, скорость звука в воздухе зависит от его абсолютной температуры. Чем ниже температура воздуха, тем меньше скорость воздуха в нем.

С подъемом на высоту, когда температура воздуха уменьшается, скорость звука тоже уменьшается. Для вычисления скорости звука на данной высоте до Н=11000м можно пользоваться формулой

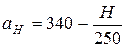, (10.3.)

где Н – высота в метрах.

Из формулы (10.2.) видно, что с уменьшением температуры воздуха его сжимаемость увеличивается, а скорость звука уменьшается. Следовательно, с подъемом на высоту сжимаемость воздуха увеличивается, т.е. на высоте воздух легче сжать, чем у земли. Из опыта следует, что величина сжатия воздуха прямо пропорциональна скорости полета и обратно пропорциональна скорости звука. Параметром, характеризующим свойство сжимаемости, является число М.

Отношение скорости полета к скорости звука на данной высоте называется числом М.

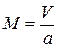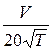или (10.4.)

Из формулы (10.4.) видно, что при постоянной скорости полета воздух перед самолетом будет сжат тем сильнее, чем меньше его температура.

Для определения числа М в полете существует специальный прибор – указатель числа М.

Изменение параметров воздуха ρ, Т и Р при увеличении скорости его течения. Рассмотрим струйку воздуха, скорость течения которой непрерывно увеличивается.

На основании уравнения Бернулли для условий сжимаемости

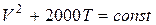(10.5.)

видно, что при увеличении скорости воздуха V, уменьшается его

температура Т, т.к. увеличение кинетической энергии воздуха происходит за счет уменьшения его внутренней энергии. Уменьшение температуры воздуха в струйке вызывает уменьшение скорости распространения звука в ней. Поэтому, говоря о скорости звука в струйке, необходимо добавлять слово «местная» т.к. речь идет о скорости звука в данном месте струйки. Изменение параметров воздуха вдоль струйки рассматриваем как адиабатический процесс. В этом случае связь между температурой и давлением выражается уравнением:

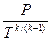= const (10.6.)

Из которого (10.6.) следует, что уменьшение температуры вызывает уменьшение давления. При понижении давления уменьшается его потенциальная энергия давления.

С увеличением скорости возрастает кинетическая энергия воздуха за счет уменьшения потенциальной энергии давления и за счет уменьшения внутренней тепловой энергии т.е. при увеличении скорости в условиях сжимаемости в струйке падает давление Р и температура Т.

Плотность воздуха вдоль струйки изменяется под действием двух факторов: изменения давления и температуры. Увеличение скорости вдоль струйки сопровождается уменьшением давления, а с уменьшением давления воздух в струйке расширяется, следовательно, его плотность уменьшается. Понижение температуры воздуха при адиабатическом течении происходит вследствие того, что внутренняя энергия воздуха расходуется на расширение и проталкивание его вдоль струйки. Следовательно, уменьшение температуры при адиабатическом течении воздуха сопровождается его расширением и уменьшением плотности. Таким образом , в результате увеличения скорости в трансзвуковом потоке давление, температура и плотность воздуха в струйке уменьшаются.

.Распространение слабых возмущений. Если источник возмущения неподвижен, то звуковые волны создаваемые им распространяются в виде концентрических сферических поверхностей, центром которых служит источник (рис.10.1).

При скорости источника, равной скорости звука (V=а), источник движется вместе с созданными им звуковыми волнами. В этом случае пространство, в котором движется источник, разделяется на две части: невозмущенную, расположенную перед источником, и возмущенную, расположенную за источником. Все возмущения (звуковые волны) концентрируются в плоскости источника и за ним. Плоскость, разделяющая невозмущенное и возмущенное пространства, называется граничной волной слабых возмущений. При V=а граничная волна представляет собой плоскость,

перпендикулярную направлению движения источника.

Когда источник движется со сверхзвуковой скоростью (V>а), он обгоняет звуковые волны созданные им. Все слабые возмущения концентрируются позади источника внутри конуса слабых возмущений. Граничная волна в этом случае представляет собой коническую поверхность. Эти поверхности называются волнами возмущения или волнами Маха.. Угол, заключенный между направлением движения источника слабых возмущений и граничной волной называется углом возмущения μ или углом Маха.

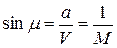(10.7.)

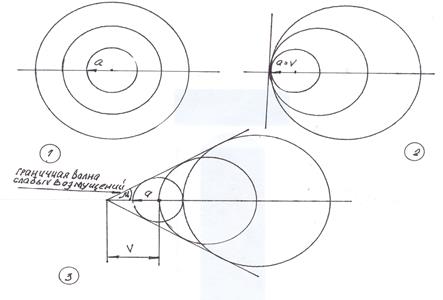
Рис.10.1. Распространение слабых возмущений. 1- источник возмущений неподвижен или движется с малой скоростью; 2 - источник возмущений движется со скоростью звука; 3 - источник возмущений движется со сверхзвуковой скоростью.
где μ – угол возмущения. Угол μ обратно пропорционален числу М. Следовательно, чем больше скорость источника возмущений тем меньше угол μ.

Скачок уплотнения или ударная волна это область характерная для сверхзвукового течения газа, в которой происходит резкое уменьшение его скорости и соответствующий рост давления, температуры и плотности. В скачке уплотнения фронт этих изменений сохраняет неизменное положение относительно тела в течении того времени, пока оно обтекается установившемся потоком. Толщина скачка уплотнения мала, её величина примерно равна длине свободного пробега молекул и составляет10 ^-5 ÷ 10 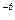⁶см. Скачки уплотнения подразделяются на прямые, косые, и местны.

Прямым называется скачок, фронт которого составляет прямой угол с направлением потока. В прямом скачке сверхзвуковой поток превращается в дозвуковой. Косой скачок образует острый угол с набегающим потоком, поток за скачком тормозится слабее, чем в прямом и с меньшими потерями механической энергии, скорость за скачком может остаться сверхзвуковой. Скачки уплотнения, создаваемые носовой частью тела, называются головными, создаваемые кормовой частью – хвостовыми. Местные скачки уплотнения образуются на поверхности тела, подразделяются на верхние и нижние.

Критическое число М. Скорость полета самолета, при которой наибольшая местная скорость обтекания на крыле по величине становится равной местной скорости звука, называется критической скоростью. Число М, соответствующее критической скорости полета называется критическим.

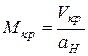(10.8.)

где V_кр - критическая скорость полета;

а_Н - скорость звука, в этом потоке на данной высоте.

Критическое число М- важный параметр в летной эксплуатации. При достижении критического М на крыльях самолёта образуются скачки уплотнения, а это вызывает изменение характеристик устойчивости и управляемости. Для обеспечения безопасности полётов на транспортных самолётах вводится ограничение по числу М. Для улучшения эксплутационных характеристик самолёта желательно увеличить критическое число М. Это можно сделать, зная влияние параметров крыла на изменение критического числа М.

Влияние формы профиля крыла на М_кр. Изменение относительной толщины и относительной кривизны профиля приводит к изменению поперечных сечений струек, обтекающих крыло данного профиля. Увеличение 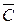и 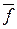вызывают уменьшение поперечных сечений струек и увеличение скорости обтекания профиля и, следовательно, уменьшение М_кр.

Уменьшение относительной толщины 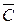и относительной кривизны 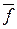профиля ведет к увеличению М_кр. При расположении наибольшей толщины профиля на 40-50% хорды число М_кр профиля увеличивается, а на 20-25% - уменьшается, поэтому скоростные профили имеют наибольшую толщину на 40-50 % хорды крыла.

Влияние угла атаки крыла на М_кр . Изменение угла атаки ведет к тем же результатам, что и изменение формы профиля т.е. увеличение α ведет к уменьшению М_кр, а уменьшение α – к увеличению М_кр профиля крыла.

Влияние стреловидности крыла на М_кр. При движении крыла со стреловидностью χ, его подъемная сила зависит не от скорости полета, а от ее составляющей 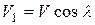В результате этого разряжение над крылом будет меньше, т.к. 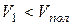. Значит и М_кр будет увеличиваться пропорционально увеличению угла стреловидности.

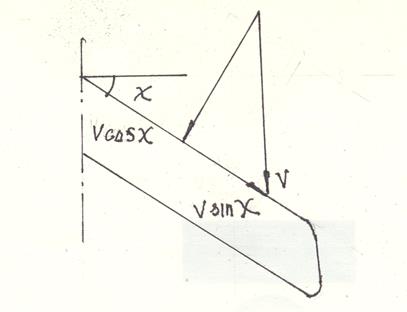
Рис. 10. 2. Влияние стреловидности крыла на М_кр.

Смешанное обтекание при наличии местных скачков обтекания.При достижении скорости равной М_кр на крыле появляются скачки уплотнения. В результате этого над профилем появляется зона дозвукового и зона

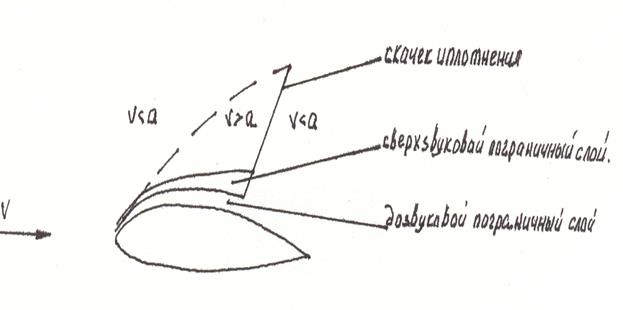
Рис.10.3.. Скачок уплотнения.

сверхзвукового потока. Зона сверхзвукового потока начинается почти у ребра атаки и заканчивается скачком уплотнения.

Точки профиля, расположенные в дозвуковом потоке у ребра обтекания являются источниками волн слабых возмущений (звуковых волн). Звуковые волны в дозвуковом потоке распространяются в виде сферических поверхностей равномерно во все стороны. По потоку звуковые волны распространяются свободно, а против потока они двигаются только до границы со сверхзвуковым потоком, где, останавливаясь, накладываются друг на друга создавая сильное возмущение – скачок уплотнения.

Вначале местный скачок возникает над профилем крыла (над крылом скорость обтекания дольше), а затем, по мере увеличения скорости полета, и под профилем. Оба скачка с ростом скорости полета перемещаются назад, при этом интенсивность их увеличивается.

Местный скачок начинается на некоторое удаление от поверхности крыла, там, где скорость пограничного слоя сверхзвуковая, поскольку непосредственно у поверхности крыла скорость частиц пограничного слоя равна нулю. Т.к. давление за скачком больше, чем перед ним, то воздух в пограничном слое, в той части слоя, где скорость потока дозвуковая, будет перемещаться против течения из области большого давления в область меньшего давления, что вызывает набухание пограничного слоя и его срыв. Это явление называют волновым срывом потому, что срыв вызван скачком – ударной волной.

Если течение в пограничном слое турбулентное, то на крыле появляется только прямой скачок уплотнения. Если течение в пограничном слое ламинарное, то вначале появляется косой скачок, за которым происходит турбулизация и отрыв пограничного слоя, в результате чего за косым скачком в области турбулентного течения пограничного слоя возникает прямой скачок уплотнения.

Этот скачок получил название λ -образного скачка. Образование косого скачка перед прямым уменьшает сопротивление, так как в этом случае поток подходит к прямому скачку с меньшей скоростью в результате потери ее при прохождении косого скачка. В этом случае прямой скачок получается менее интенсивным. Таким образом, комбинация прямого и косого скачка дает меньше сопротивления, чем один прямой скачок.

С другой стороны за косым скачком происходит более ранний отрыв потока от крыла. Это приводит к уменьшению разряжения над крылом, т.е. к уменьшению С_у.

При увеличении скорости полета происходит перемещение местных скачков уплотнения к ребру обтекания крыла, в результате чего происходит перемещение центра давления назад, а полная аэродинамическая сила, перемещаясь к ребру обтекания, отклоняется назад, уменьшая угол наклона.

Смешанное обтекание при наличии головных и хвостовых скачков уплотнения.

При скорости полета больше скорости звука лобовая часть профиля тормозит набегающей сверхзвуковой поток. Поэтому впереди крыла находится небольшая часть дозвукового потока, в которой могут распространятся волны слабых возмущений (звуковые волны), созданные точками лобовой части крыла. Звуковые волны в дозвуковом потоке распространяются против потока до границ сверхзвукового потока, где образуют головной скачок уплотнения. Одновременно с возникновением головного скачка на крыле образуются местные скачки уплотнения или хвостовые скачки. Местные скачки с ростом числа М полета сдвигаются назад. Дойдя до ребра обтекания, они останавливаются, превращаясь в хвостовой скачок.

Форма и положение головного скачка уплотнения зависят от числа М полета и формы головной части тела. Если тело тупое, головной скачок состоит из участка прямого скачка, который переходит в косые скачки, а затем, вдали от тела, в граничную волну слабых возмущений. Чем острее головная часть тела, тем меньше протяженность прямого участка и тем меньше угол наклона скачка, тем головной скачок ближе к ребру атаки тела и тем меньше волновое сопротивление. При клинообразном профиле головной скачок не имеет прямого участка и сидит на носке профиля, что даёт минимальное волновое сопротивление.

Увеличение числа М полета приводит к уменьшению прямой части головного скачка, к уменьшению его наклона, и приближению головного скачка к ребру атаки.

При сверхзвуковом полете требуются клиновидные, ромбовидные или чечевицеобразные профили. В этом случае головной скачок располагается на носке крыла, т.е. он является присоединенным, в результате чего сопротивление профиля уменьшается.

Волновое сопротивление крыла.Процесс возникновения и развития на крыле местных скачков уплотнения, а так же: развитие волнового срыва потока, вызванного скачками, называется волновым кризисом крыла. Критическое М характеризует начало развития на крыле волнового кризиса. Увеличение скорости, свыше критической, приводит к появлению нового дополнительного вида сопротивления, названного волновым сопротивлением крыла.

В таком случае лобовое сопротивление крыла состоит из профильного, индуктивного и волнового сопротивления. Волновое сопротивление есть сопротивление давления, т.к. оно обусловлено повышенной разностью давлений перед крылом и за крылом. Указанное дополнительное сопротивление крыла названо волновым потому, что процесс появления сверхзвуковых зон обтекания сопровождается возникновением ударных волн или скачков уплотнения.

С энергетической точки зрения волновое сопротивление есть результат торможения потока воздуха на скачке уплотнения. При этом кинетическая энергия потока необратимо затрачивается на нагревания воздуха в скачке. Вследствие того, что торможение потока на прямом скачке больше, чем на косом, величина волнового сопротивления крыла зависит от формы скачков, расположенных на нем. С увеличением скорости полёта уменьшается наклон косого скачка, торможение воздушного потока в нем уменьшается, а значит, будет уменьшаться и волновое сопротивление.

Влияние сжимаемости на аэродинамические характеристики прямого крыла. Рассмотрим зависимость лобового сопротивления от скорости полёта (рис.10.4.). При дозвуковом обтекании крыла С_х не зависит от числа М, то есть сжимаемость не оказывает влияние на величину лобового сопротивления. При увеличении скорости полета выше Мкр_крит в результате волнового срыва С_х резко увеличивается. Наибольшего значения С_х достигает при M=1÷1,2 (для прямого крыла). Дальнейшее увеличение скорости ведет к появлению головного и хвостового скачков уплотнения, угол наклона которых уменьшается. Поэтому уменьшается и волновое сопротивление, а значит и С_х. На прямом крыле волновой кризис и увеличение лобового сопротивления происходит на меньших скоростях, чем на стреловидных, но на скоростях более двух М, разница Су прямого и стреловидного крыла незначительна.

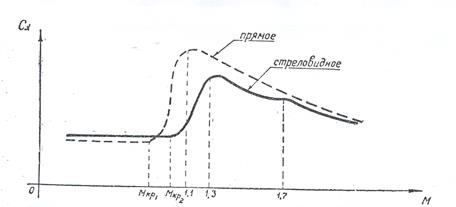
Рис.10.4. График зависимости С_х от числа М.

Зависимость С_у от числа М На скоростях полета не превышающих 0,4 М, сжимаемостью воздуха можно пренебречь, в этом случае величина разности относительных давлений по верхней и нижней частях профиля не меняется (рис.10.5 |1-2| ). При дальнейшем увеличении скорости от М=0,4 до М_кр разряжение под крылом увеличивается, увеличивается и С_у( (рис10.5 |2-3|) В результате образования скачка уплотнения на верхней части профиля разность относительных давлений продолжает увеличиваться, что ведет к дальнейшему росту С_у (рис.10.5 |3-4|)

Образование скачка уплотнения по нижней части профиля приводит к уменьшению разности давления, и следовательно, к уменьшению С_у (рис.10.5. |4-5| ) При дальнейшем увеличении М полета нижний скачок уплотнения сходит с крыла, превращаясь в хвостовой скачок уплотнения. Величина разности относительных давлений снова возрастает до М=1÷1,2, возрастает и Су (рис.10.5 |5-6|), при дальнейшем увеличении скорости (более М=1÷1,2) разность относительных давлений 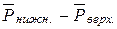уменьшается, уменьшается и С_у( рисю10.5 |6-7| ).

Аэродинамические характеристики стреловидного крыла. Как уже выяснено стреловидность крыла увеличивает критическое число М и уменьшает рост волнового сопротивления, так как скачок уплотнения на таком крыле обладает меньшей интенсивностью, чем на прямом крыле с той же относительной толщиной 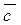, при той же скорости полета и на том угле атаки. Набегающий поток подходит к передней кромке крыла под углом

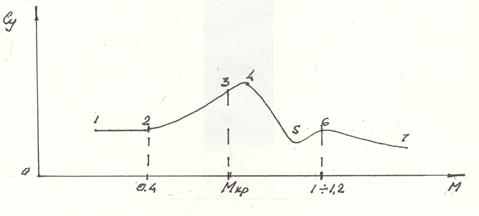
Рис.10.5 График зависимости С_у от числа М

( при виде сверху ) т.е. является косым, а это уменьшает интенсивность скачка.

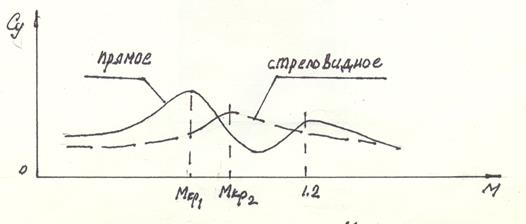Рис.10.6. График зависимости Су от числа М для прямого и стреловидного крыльев.

Особенностью обтекания стреловидного крыла является наличие зоны пониженных разряжений на передней кромке крыла и зона увеличенных разряжений на задней кромке крыла. В результате этого общее разряжение в центральной части крыла уменьшается, точка наибольшего разряжения смещается назад и уменьшается подъёмная сила по сравнению с концевыми сечениями крыла. На концевых сечениях крыла разрежение увеличивается, следовательно, увеличивается подъёмная сила, а точка наибольшего разряжения смещается вперёд. Исходя из сказанного видно, что Мкрит. центральной части крыла увеличивается за счёт меньшего разряжения, а Мкрит. концевых сечений уменьшается за счёт увеличенного разряжения. По этим причинам волновой кризис стреловидного крыла начинается на его концевых сечениях. Таким образом, подъёмная сила стреловидного крыла распределяется неравномерно: Укр. растет от центральных к концевым сечениям, у прямоугольного крыла, наоборот – в центральной части крыла подъёмная сила имеет максимальное значение уменьшаясь к концевым сечениям. Сопротивление по размаху стреловидного крыла тоже неравномерно: в центральных сечениях крыла сопротивление больше, чем в концевых сечениях. Ввиду уменьшения разряжения в центральной части крыла и увеличения его в концевых сечениях воздух в пограничном слое перетекает вдоль его размаха к концевым сечениям. .Неравномерное распределение подъемной силы, перетекание воздуха в пограничном слое вдоль размаха и особенности распределения давления на концевых сечениях приводят к набуханию пограничного слоя и его преждевременному срыву с концов стреловидного крыла по сравнению с прямым крылом. Срыв потока с концов стреловидного крыла ухудшает устойчивость и управляемость самолета на больших углах атаки.

Коэффициент С_у стреловидного крыла при дозвуковом и смешанном (трансзвуковым) обтекании меньше чем у прямого крыла, но характер его изменения более благоприятен (отсутствуют провалы). При сверхзвуковом обтекании С_у прямого и стреловидного крыла мало отличаются друг от друга (Рис10.6).

На рис.10.7. показаны характеристики 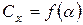для различных крыльев. На нем видно что М_кр для стреловидного крыла больше, чем для прямого. При смешанном обтекании т.е. при М>М_кр волновое сопротивление крыла создается в основном его центральными сечениями, поэтому наибольшее значение С_х стреловидного крыла будет меньше чем прямого. Уменьшение С_х после М=1,2 объясняется уменьшением угла наклона головных скачков уплотнения. При М≈1,7 вся передняя кромка стреловидного крыла становится сверхзвуковой, то есть фронт головного скачка совпадает с передней кромкой крыла. В этом случае волновое сопротивление крыла возрастает за счет концевых сечений крыла. Начиная с чисел М=2÷2,5 преимущество применения стреловидного крыла по сравнению с прямым отсутствует.

Стреловидность улучшает аэродинамические характеристики крыла при дозвуковом и трансзвуковом (смешанном) обтекании, а значит в этом диапазоне скоростей стреловидное крыло имеет преимущество перед прямым крылом.

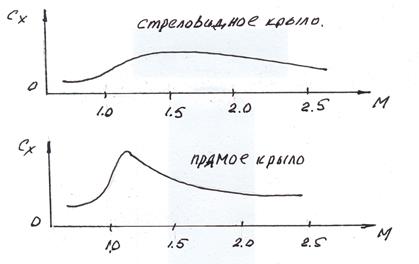
Рис.10.7. График зависимости С_х от М для прямого и стреловидного крыльев.

Особенности аэродинамики крыла малого удлинения. Для получения выигрыша в величине М_кр – удлинение крыла должно быть меньше 2÷2,5 при этом в секторе обтекания крыла наблюдается интенсивное перетекание воздуха на торцах, уменьшающие наибольшее разряжение под крылом. Поэтому на малых числах М применяются крылья с большим удлинением (С_у выше), а при М>2 различие в величине С_у небольшое, так же мало различий и в коэффициентах С_х. Но с точки зрения уменьшения

веса, увеличения жесткости и прочности на М=2÷2,5 имеют преимущества крыла малых удлинений.

Контрольные вопросы .

1. Напишите формулу скорости звука.

2. Как влияет сжимаемость воздуха на скорость звука ?

3. За счёт чего возрастает кинетическая энергия потока с увеличением его скорости ?

4. Что такое волна возмущения ?

5. Как зависит угол μ от числа М ?

6.Чем характеризуется критическая скорость самолёта ?

7.Как изменяется величина Мкрит. при уменьшении угла атаки крыла ?

8. Как образуется скачок уплотнения ?

9. Объясните причину возникновения волнового сопротивления ?

10. В чём заключается преимущество стреловидного крыла перед прямоугольным на трансзвуковых скоростях ?

Воздушные винты.

Воздушный винт служит для преобразования крутящего момента двигателя М.кр в силу тяги необходимую для поступательного перемещения самолета.

Составные части воздушного винта фиксированного шага(ВФШ).Составные части воздушного винта фиксированного шага(ВФШ) указаны на рис.11.1.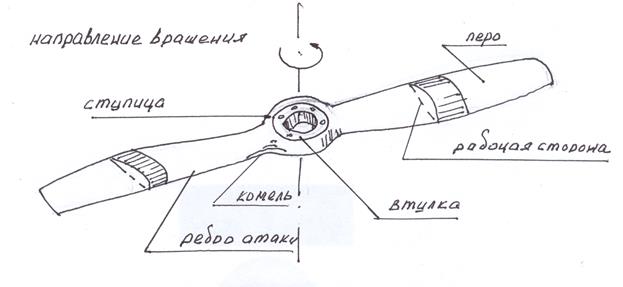

Рис.11.1. Основные части воздушного винта фиксированного шага.

Классификация воздушных винтов. Воздушные винты классифицируются:

- по числу лопастей;

- по материалу изготовления;

- по роду действия (тянущие, толкающие);

- по направлению вращения;

- по способу крепления лопастей к втулке винта (винт фиксированного шага – ВФШ, винт изменяемого шага ВИШ).

Винты изменяемого шага могут быть флюгерными, реверсивными и соосными.

Основными формами лопастей воздушных винтов (Рис. 11. 2.) являются:

- веслообразные;

- симметричные;

- саблевидные.

Рис 11.2. Основные формы лопастей воздушных винтов.

Геометрические характеристики ВВ. Лопасть воздушного винта по своим геометрическим характеристикам соответствует характеристикам крыла, поэтому основными геометрическими характеристикам ВВ являются:

- профиль лопасти;

- хорда, средняя линия;

- относительная толщина ;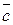

- относительная кривизна ;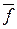

- относительный радиус элемента лопасти ¯r - -угол установки лопасти φ;

- диаметр винта ( D);

- ометаемая площадь винта.

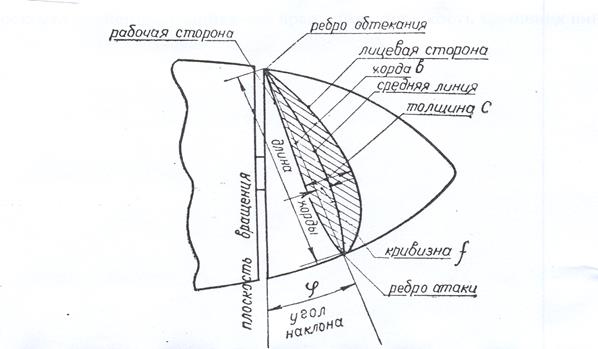
Рис. 11.3. Геометрические характеристики воздушного винта (ВВ).

Относительным радиусом элемента лопасти ¯r называется отношение радиуса элемента r к радиусу винта R: ¯r = r / R (11.1)

Угол установки лопасти винта (φ) называется угол, заключенный между плоскостью вращения и хордой элемента лопасти винта.

Угол установки замеряется на расстоянии 0,75 радиуса винта. Лопасть имеет геометрическую крутку, поэтому углы установки, по мере удаления элементов лопасти витка от комлевой части, уменьшаются.

Диаметром винта ( D) является диаметр окружности, по которой движутся концы лопастей.

Площадь, ометаемая винтом – есть площадь круга, который описывают концы лопастей.

Плоскость перпендикулярная оси вращения – плоскость вращения винта

Кинематические характеристики ВВ

Геометрический шаг винта (Н) – расстояние, проходимое ВВ за один оборот в твердой среде.

Н = 2πrtgφ; (11.2.)

Поступь винта (На) - расстояние, проходимое ВВ за один оборот в воздухе

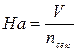; ( 11.3.)

где V - скорость полета;

п_сек - частота вращения ВВ в секунду.

Относительная поступь (λ)

λ = На / D = V / D n сек ( 11.4)

скольжение(S ) – разность между геометрическим шагом и поступью.

S =H – Ha = H – V / D n сек ; (11.5.)

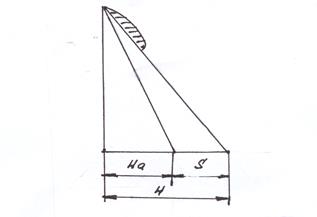
Рис. 11.4. Кинематические характеристики ВВ.

Аэродинамические силы ВВ (Рис.11.5.) Лопасть винта находится под воздействием:

- окружной скоростиU;

- поступательной скоростиV;

- результирующей скоростиW;

Эти скорости образуют треугольник скоростей со следующими углами: -угол, заключенный между результирующей скоростью W и хордой элемента лопасти называется углом атаки α;

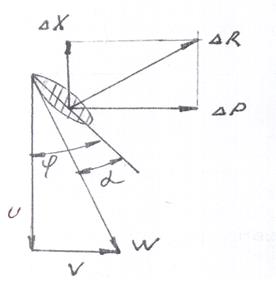
Рис.11.5. Аэродинамические силы

элемента лопасти.

- угол заключенный между плоскостью вращения (окружной скоростью и) и хордой элемента лопасти называется углом установки лопасти φ.

При обтекании лопасти воздушным потоком на каждом элементе лопасти возникает полная аэродинамическая сила элемента лопасти ∆R.

При разложении этой силы ∆R на составляющие получаем:

- в направлении параллельном оси вращения ВВ – элементарную силу тяги (∆Р);

- в направлении противоположном вращению ВВ – элементарную силу – силу сопротивления (∆Х).

Сумма элементарных сил тяги составляет силу тяги винта и определяется по формуле:

P = αrn 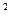D 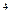(11.6.)

где, α - коэффициент тяги, учитывающий форму профиля лопасти, относительной поступи и т.д.

ρ - плотность воздуха;

D - диаметр винта;

n - частота вращения.

На самолете Ан-2 при работе на земле, на взлетном режиме тяга винта составляет 1500 кгс., АВ-2 - 1850 кгс., В.509-Д-94 – 1600 кгс.

Сумма элементарных сил сопротивления винта составляют силу сопротивления вращению лопасти винта (Х).

Сила сопротивления на плече r создает момент реактивный М реакт. винта (рис.11.6).

М_{реакт =} Х_вр.л. r к _(11.7.)

где Х_вр.л. – сопротивление лопасти

r - радиус точки приложения силы;

к - количество лопастей.

Крутящий момент Мкр. – затрачивается на преодоление момента сопротивления винта Мреакт. т.е. Мкр. = Мреакт.

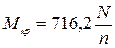(11.8.)

где N - мощность двигателя;

п - частота вращения;

Мкр. -_--крутящий момент двигателя.

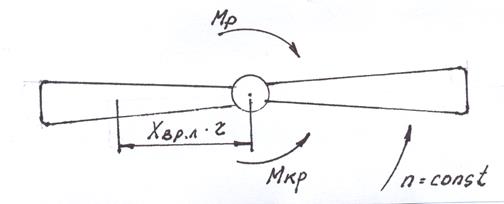
Рис.11.6. Аэродинамические силы и моменты ВВ.

Тяга ВВ. Влияние скорости полета, частоты вращения, высоты полета, угла установки лопасти φ на силу тяги ВВ.

Скольжение и поступь характеризует способность создавать тягу ВВ. На скорости равной нулю скольжение максимально и тяга ВВ максимальна. С увеличением скорости полета скольжения уменьшается и уменьшается тяга ВВ.

Положительное скольжение – положительная тяга. На больших скоростях скольжение может стать отрицательным, т.е. ВВ проходит расстояния больше чем его геометрический шаг. Отрицательное скольжение – отрицательная тяга.

При скольжении S = 0 воздух не отбрасывается, тяга равна нулю. Отсюда следует, что с увеличением скорости полета угол атаки лопастей все время уменьшается, а сила R изменяет свою величину и направление, все время поворачиваясь против часовой стрелки таким образом, что ее составляющая сила тяги Р - уменьшается до нуля, а затем ставится отрицательной т.е. при работе винта на месте угол атаки α максимальный и тяга максимальная, при увеличении скорости полёта тяга уменьшается (рис.11.7).

Влияние частоты вращения ВВ на тягу винта видно из формулы(11.6.), где тяга пропорциональна квадрату частоты вращения винта, но это справедливо только

до того, как скорость обтекания лопасти достигнет местной скорости звука (Рис.11.10.).

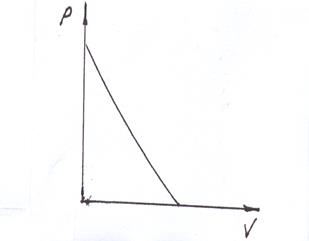
Рис. 11.7. График зависимости тяги ВВ от скорости полёта.

Если самолет летит с постоянной скоростью, а частота вращения винта увеличивается

то скольжение увеличивается, углы атаки растут, растёт и тяга (рис. 11. 8.).

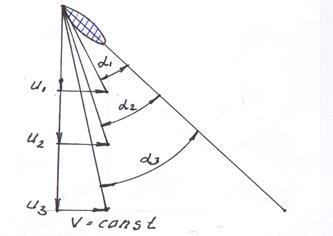
Рис. 11.8. Изменение угла атаки в зависимости от увеличения п_сек ВВ.

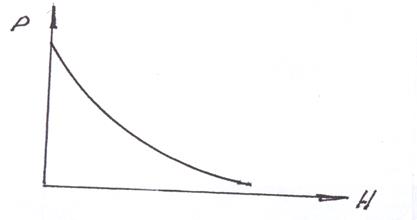
Рис. 11. 9. График зависимости силы тяги ВВ от высоты полета.

С увеличением высоты полета, в связи с уменьшением массовой плотности воздуха аэродинамические силы, а в частности, тяга ВВ уменьшается (Рис 10.9) Зависимость угла атаки, а значит и тяги ВВ от угла установки прямая – увеличение угла установки φ, увеличивает α и Р винта.

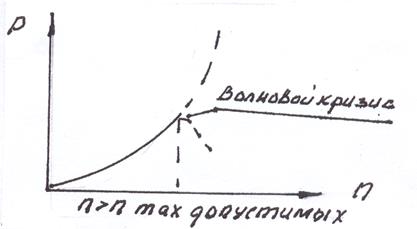
Рис. 11. 10. График зависимости Р от частоты вращения ВВ.

Полезная мощность ВВ

Полезной мощностью (тяговой мощностью) называется работа силы тяги за одну секунду.

А_{сек =} Ν_тв = PV; (11.9.)

где А_сек - работа силы тяги;

Ν_тв - полезная мощность (тяговая мощность) винта;

Р - сила тяги винта;

V - скорость самолета.

Мощность, развиваемая винтом, называется полезной потому, что она затрачивается на полезную работу – передвижение самолета в воздухе.

Из формулы (11.9.) видно, что при V=0, полезная мощность (тяговая мощность) равна нулю N=0, при определенной скорости называемой расчетной, произведение PV максимальное, при дальнейшем увеличении скорости полета, тяга падает до нуля и на этой скорости полезная мощность равна нулю.

При постоянной скорости полёта и увеличении частоты вращения ВВ увеличивается тяга (Рис 11.8) и полезная мощность воздушного винта, при уменьшении частоты вращения ВВ тяга и полезная мощность уменьшается.

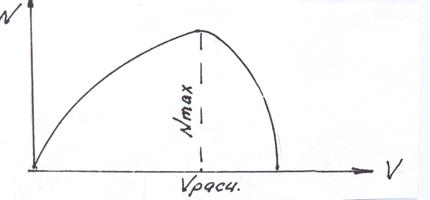
Рис.11.11. График зависимости полезной мощности от скорости полёта.

Мощность, потребная на вращение винта. Мощность, необходимая для преодоления работы сил сопротивления вращению винта за единицу времени называется мощностью, потребной на вращение винта.

N = KXв U (11.10.)

где Х_в - сила сопротивления вращению лопасти винта;

U - окружная скорость;

К - количество лопастей винта.

Для данного винта мощность потребная на вращение N_пВ зависит от:

- скорости полета;

- высоты полета;

- частоты вращения ВВ;

С увеличением скорости полета, угол атаки лопастей уменьшается, поэтому сопротивление Х_в и потребная мощность Nп.в. также уменьшается. С увеличением частоты вращения ВВ, при постоянной скорости полёта, окружная скорость увеличивается, увеличиваются и углы атаки лопастей, поэтому увеличиваются сопротивление винта и мощность потребная на вращение винта. С увеличением высоты полета плотность воздуха уменьшается, а следовательно уменьшается сопротивление и потребная мощность.

Мощность, которая снимается с носка вала называется эффективной мощность Nе. Для того, чтобы при определенной V и H двигатель поддерживал постоянную частоту вращения необходимо, чтобы эффективная мощность двигателя была равна мощности, потребной на вращение винта.

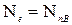(11.11.)

Коэффициентом полезного действия ВВ. Коэффициентом полезного действия (КПД) винта называется отношение полезной мощности (тяговой мощности) винта к эффективной мощности двигателя

ηв = Ν_{тв /} Nе; (11.12.)

Максимальный КПД современных винтов равен 0,8÷0,9.

На КПД ВВ влияют профиль и форма лопасти в плане. Больший КПД имеют тонкие симметричные профили с симметричной формой лопасти в плане т.к. у таких лопастей профильное и индуктивное сопротивление меньше, чем у толстых профилей. На КПД ВВ также влияют скорость, высота полета и частота вращения ВВ. При изменении скорости, высоты полета и частоты вращения ВВ, но при постоянной эффективной мощности двигателя, КПД винта меняется также как и полезная мощность винта (Рис 11.11) При увеличении скорости полета от 0 до расчетной скорости КПД (рис.11.12)

растет за счет увеличения относительной поступи λ, при увеличении скорости выше V расчетной, КПД падает в результате возрастания волновых потерь на концах лопасти и падения силы тяги. Увеличение КПД на больших скоростях полёта можно добиться увеличением Мкрит. лопасти и уменьшением частоты вращения ВВ. Мкрит. лопасти увеличивается за счет уменьшения относительной толщины профиля лопасти, для чего делают широкие, прямоугольные концы лопастей. Возможно придание лопасти саблевидной формы в плане. В этом случае лопасть работает аналогично стреловидному крылу.

Для уменьшения скорости обтекания лопасти уменьшают частоту вращения ВВ, чем добиваются уменьшения волнового сопротивления. Для этой цели применяются редукторы, которые уменьшают частоту вращения винта, не меняя частоту вращения двигателя. Для предотвращения падения тяги с увеличением скорости полёта применяют винты изменяемого шага о которых речь пойдёт в дальнейшем.

Работа винта фиксированного шага (ВФШ) на различных режимах. При постоянной частоте вращения винта мощность двигателя Nе равна мощности потребной на вращение винта N п.в.. При увеличении скорости полёта Nе и N п.в. меняются. Эффективная мощность поршневых двигателей с увеличением скорости полета немного увеличивается, (Рис.11.13) а мощность потребная на вращение винта с увеличением скорости, уменьшается т.к. уменьшаются силы сопротивления вращению винта (уменьшается угол атаки α винта и, следовательно, индуктивное сопротивление.)