Раздел 2. Случайные события и их вероятности.

Будем называть испытанием (опытом, наблюдением, измерением) некоторую совокупность действий. Предполагается, в общем случае, что испытание можно повторить неограниченное число раз.

Событием (случайным событием) называется всякий факт, который может произойти или не произойти в результате опыта. События обозначаются буквами А, B, C, D, …

Вероятностью события называется численная мера возможности появления события в результате данного опыта. Вероятность события А обозначается Р(А). Событие W, которое обязательно произойдет в результате опыта, называется достоверным: Р(W) = 1. Событие Æ, которое никогда не может произойти в результате опыта, называется невозможным: Р(Æ) = 0. Событие А, о котором нельзя заранее сказать произойдет оно или нет в результате опыта, называется случайным: 0£Р(А)£1.

Суммой событий А+В называется событие, состоящее в осуществлении хотя бы одного из событий А или В (безразлично, какого именно, или обоих, если это возможно).

События А и В называются несовместными, если они не могут произойти одновременно при одном и том же испытании. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).

Два случайных события называются противоположными, если появление одного из них равносильно непоявлению другого. Если одно из этих событий обозначить А, то другое (противоположное) обозначают А (читается «не А»). Событие А означает, что А не произошло: Р(А)+Р(А)=1.

Произведением двух событий АВ называется событие, состоящее в том, что оба события произошли одновременно. Если появление каждого из событий не зависит от того, произошло или нет другое, то события называются независимыми, и вероятность их произведения равна произведению вероятностей этих событий: Р(АВ)=Р(А)×Р(В).

Если вероятность появления события В изменяется в зависимости от того, произошло или нет событие А, то такие события называются зависимыми. Вероятность события В при условии, что событие А уже произошло, обозначается 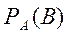. Вероятность произведения зависимых событий определяется формулой .

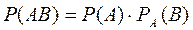Если события А и В несовместные, то Р(АВ)=0.

Формула для вычисления вероятности суммы двух событий, все равно каких, совместных или нет, имеет вид: Р(А+В)=Р(А)+Р(В)-Р(АВ).

Полной группой событий называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них.

Несколько событий в данном опыте называются равновозможными, если нет оснований считать какое-либо из них более возможным, чем другое. События 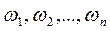называются элементарными, если они образуют полную группу событий, несовместны (то есть никакие два из них не могут произойти одновременно) и равновозможны. Если некоторое событие А происходит в результате появления одного из элементарных событий 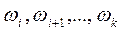, то эти элементарные события называются благоприятствующими событию А.

Классическое определение вероятности. Пусть в результате опыта может произойти одно из n элементарных событий, причем событию А благоприятствуют m из них (m£n). Тогда вероятностью события А называется отношение числа элементарных исходов, благоприятствующих появлению события А, к общему числу равновозможных элементарных исходов: Р(А)= m/n.

Пример. Из пяти букв разрезной азбуки составлено слово ДОМИК. Ребенок, не умеющий читать, рассыпал эти буквы и затем выложил три из них в произвольном порядке. Найти вероятность того, что у него получилось слово КОД. (Предполагается, что ребенок не переворачивает буквы.)

Решение. Пусть случайное событие А состоит в том, что получено слово КОД. Число равновозможных элементарных исходов равно числу размещений из 5 элементов по 3: .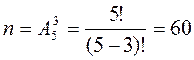

Поскольку все буквы в первоначальном слове разные, то среди 60 исходов не будет двух одинаковых, то есть слово КОД встречается только один раз: m=1, Р(А)=1/60.

В некоторых случаях не удается перечислить или посчитать все элементарные и благоприятствующие исходы. Тогда принимается какая-либо другая мера подсчета (например, площадь фигуры или объем тела). Такие вероятности называются геометрическими. Если обозначить W - пространство элементарных исходов, то можно записать .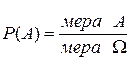

Пример. В круг радиуса R вписан квадрат. Из круга наудачу выбирается точка. Какова вероятность того, что эта точка лежит внутри квадрата?

Решение. Событие А состоит в том, что наудачу выбранная из круга точка оказалась лежащей внутри квадрата. Понятно, что посчитать количество точек внутри круга и внутри квадрата невозможно, поэтому мерой числа равновозможных элементарных исходов будет площадь круга 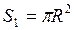, а мерой числа благоприятных исходов – площадь квадрата .

.

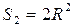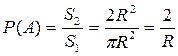Рассмотрим различные примеры решения задач с применением указанных выше формул.

Задача 1. В двух ящиках содержатся синие и красные шары: в первом ящике 6 синих и 7 красных, во втором ящике – 4 синих и 5 красных. Из каждого ящика извлекают по одному шару. Найти: 1) вероятность того, что хотя бы один из вынутых шаров будет красным; 2) вероятность того, что только один из шаров будет красным.

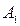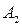Решение. Пусть событие А состоит в том, что хотя бы один их вынутых шаров красный. Обозначим за и события, состоящие в извлечении красного шара из первого и из второго ящиков соответственно. Тогда событие А будет выражено через события 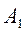и 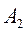формулой А= 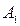+ 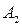, а вероятность этого события, согласно правилу нахождения вероятности суммы двух событий Р(А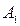)=Р( )+Р( 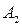) – Р( ).

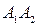События 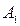и 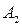- независимые, поэтому 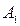Р( 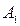)=Р( )Р( ).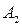

Вычислим вероятности событий. В первом ящике находится 13 шаров, из них 7 красные, следовательно Р( 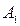)=7/13. Во втором ящике = 9 шаров, из них 5 – красные, то есть Р( 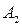)= 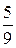. Р(А)= 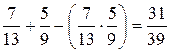. Этот же результат можно было получить, рассматривая противоположное событие`А, состоящее в том, что ни один из вынутых шаров не оказался красным: `А=` 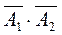, , 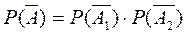Р(А)=1-Р(`А) . Подставив числовые значения 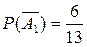, , 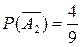получим .

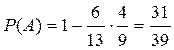Пусть событие В состоит в том, что только один из вынутых шаров оказался красным 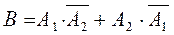. События 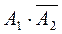и 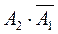несовместные, поэтому , .

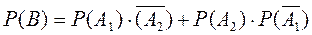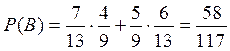Задача 2 (задача о выборке). В лотерее 10 билетов, из них 4 выигрышных. Найти вероятность того, что среди взятых наугад пяти билетов будут два выигрышных.

Решение. Пусть А – событие, состоящее в том, что среди выбранных наудачу пяти билетов оказались два выигрышных. По классическому определению вероятностей Р(А)=m/n, где n – число способов, которыми из 10 имеющихся билетов можно выбрать любые 5 все равно в каком порядке: n=. Число благоприятных исходов m равно числу способов, которыми можно выбрать два выигрышных билета из четырех имеющихся и еще три невыигрышных билета из шести: m=Р(А).

Теоретические вопросы к разделу 2.

1. Понятие случайного, достоверного и невозможного событий.

2. Вероятность суммы и произведения событий.

3. Классическое определение вероятности.

Задание к разделу 2.

а) Студент знает k вопросов из n вопросов программы. Экзаменатор задает три произвольных вопроса из имеющихся. Найти вероятность того, что студент знает ответы а) на все три вопроса; б) только на два вопроса; в) только на один вопрос; г) не знает ответа ни на один из заданных вопросов.

№
n
k

б) Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 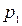, вторым - 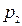, третьим - 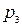. Найти вероятность того, что: а) только два стрелка попали в цель; б) все три стрелка попали в цель.

№
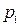	0,9	0,6	0,7	0,9	0,7	0,6	0,5	0,4	0,5	0,7
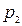	0,8	0,7	0,6	0,5	0,8	0,4	0,7	0,7	0,6	0,4
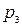	0,7	0,8	0,5	0,7	0,7	0,5	0,8	0,9	0,9	0,9