Теория вероятностей. Случайные события.
КОНТРОЛЬНАЯ РАБОТА № 4
Теория вероятностей. Случайные события.
Случайные величины.
Методические указания и задания
Задание к разделу 2.
а) Студент знает k вопросов из n вопросов программы. Экзаменатор задает три произвольных вопроса из имеющихся. Найти вероятность того, что студент знает ответы а) на все три вопроса; б) только на два вопроса; в) только на один вопрос; г) не знает ответа ни на один из заданных вопросов.
| № | ||||||||||
| n | ||||||||||
| k |
б) Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна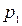 
, вторым - 
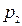, третьим - 
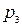. Найти вероятность того, что: а) только два стрелка попали в цель; б) все три стрелка попали в цель.
| № | ||||||||||
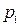 | 0,9 | 0,6 | 0,7 | 0,9 | 0,7 | 0,6 | 0,5 | 0,4 | 0,5 | 0,7 |
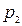 | 0,8 | 0,7 | 0,6 | 0,5 | 0,8 | 0,4 | 0,7 | 0,7 | 0,6 | 0,4 |
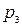 | 0,7 | 0,8 | 0,5 | 0,7 | 0,7 | 0,5 | 0,8 | 0,9 | 0,9 | 0,9 |
Задание к разделу 3.
Куплено n лотерейных билетов. Вероятность выигрыша на один лотерейный билет р=0,3. Найти а) вероятность того, что из n билетов k билетов выиграют; б) наивероятнейшее число выигрышных билетов.
| № | ||||||||||
| n | ||||||||||
| k |
Задание к разделу 4.
Дискретная случайная величина может принимать только два значения: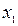 
и 
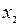, причем 
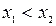. Известны вероятность 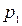возможного значения 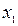, математическое ожидание М(Х) и дисперсия D(X). Найти закон распределения этой случайной величины.
| № | ||||||||||
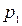| | 0,1 | 0,3 | 0,5 | 0,7 | 0,9 | 0,9 | 0,8 | 0,6 | 0,4 | 0,2 |
| М(Х) | 3,9 | 3,7 | 3,5 | 3,3 | 3,1 | 2,2 | 3,2 | 3,4 | 3,6 | 3,8 |
| D(X) | 0,09 | 0,21 | 0,25 | 0,21 | 0,09 | 0,36 | 0,16 | 0,24 | 0,24 | 0,16 |
Раздел 5. Непрерывные случайные величины.
В теории вероятностей и ее приложениях часто встречаются такие случайные величины, возможные значения которых сплошь заполняют некоторый интервал (a,b) конечный или бесконечный. Такие случайные величины называются непрерывными. Закон распределения вероятностей непрерывной случайной величины Х должен позволять находить вероятность попадания ее значений в любой интервал, Лежащий внутри (a,b). При этом вероятность попадания случайной величины в интервал (х,х+Dх) малой длины Dх>0 можно приближенно считать пропорциональной длине этого интервала: Р(х<X<x+Dх) » f(x)Dх, где функция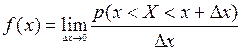 
называется функцией плотности распределения вероятностей случайной величины Х, а произведение f(x)Dх = f(x)dx – элементом вероятности.
Свойства функции плотности:
1) f(x) ³ , xÎ(-¥,+¥);
2) вероятность попадания случайной величины Х в интервал (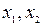 
) равна 
;
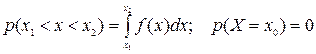3) 
.
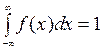Плотность распределения вероятностей вполне определяет закон распределения непрерывной случайной величины Х.
Так как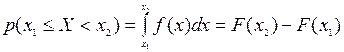 
, то функция F(x) является первообразной функции f(x): F¢(x)=f(x), откуда следует, что для непрерывной случайной величины Х функция распределения F(x) является непрерывной. Если задана функция плотности f(x), то функция распределения может быть найдена по формуле
.
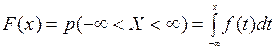Функция F(x) называется интегральной функцией, а функция f(x) – дифференциальной.
Математическим ожиданием (средним значением, центром распределения) М(Х) непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f(x):
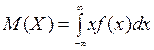
Дисперсию непрерывной случайной величины удобно вычислять по той же упрощенной формуле, что и в дискретном случае
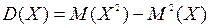, где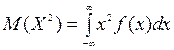 
.
Укажем некоторые из наиболее часто встречающихся законов распределения непрерывных случайных величин.
Равномерное распределение в интервале (а,b). Говорят, что случайная величина распределена равномерно в конечном интервале (а,b), если все ее возможные значения сосредоточены на этом интервале, и плотность распределения ее вероятностей на этом интервале постоянна. Функция плотности распределения задается формулой:
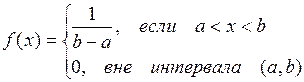
Числовые характеристики: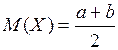 
, 
; 
.
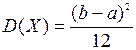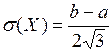Нормальный закон распределения. Плотность распределения вероятностей непрерывной случайной величины Х имеет вид:
, 
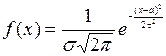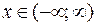, где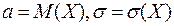 
.
Вероятность того, что случайная величина Х примет значения из интервала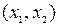 
определяется с помощью интегральной функции Лапласа
.
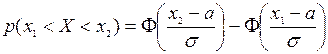Справедливо «правило трех сигм»: R(½C-а½<3s)=,9973, которое позволяет при решении практических задач применять нормальный закон распределения к случайным величинам, заданным на конечном интервале. К нормальному распределению обычно приводят задачи, связанные с распределением сумм большого числа случайных величин.
Показательный закон распределения. Плотность вероятностей определяется формулой
.
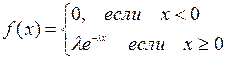Формула распределения показательного закона
.
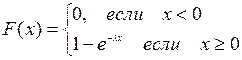Числовые характеристики: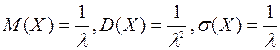 
.
К показательному закону распределения вероятностей приводит задача о распределении промежутка времени Х между двумя последовательными событиями в простейшем потоке.
Пример. Случайная величина Х задана функцией распределения
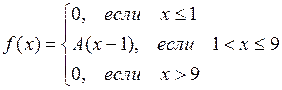
Требуется:
1) определить коэффициент А;
2) найти функцию распределения F(x);
3) схематично построить графики функций f(x) и F(x);
4) вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х;
5) определить вероятность того, что Х примет значения из интервала (8; 11).
Решение. 1)Коэффициент А можно определить из условия .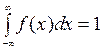
,
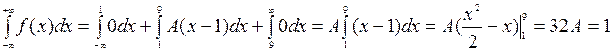откуда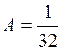 
; 
.
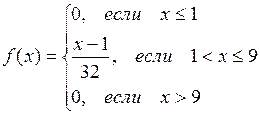2) Функцию распределения найдем из соотношения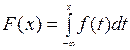 
. Если x£1, то 
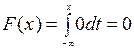; если 1<x£9, то 
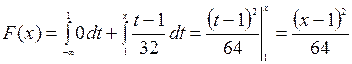; если х>9, то 
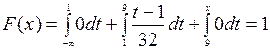. Таким образом, функция распределения имеет вид 
.
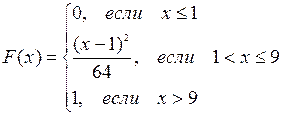3) Графики функций f(x) и F(x) изображены на рисунках.
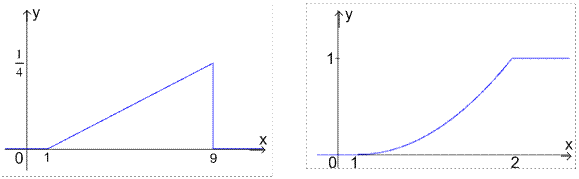
Рис 4. Функция плотности. Рис. 5. Функция распределения.
4) Найдем математическое ожидание и дисперсию случайной величины Х: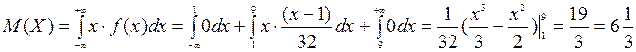 
. Для вычисления дисперсии найдем 
: 
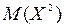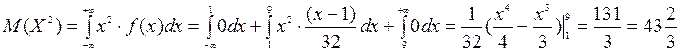Воспользуемся формулой : 
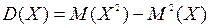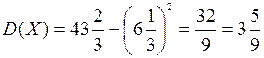. Среднее квадратическое отклонение случайной величины Х: 
.
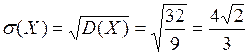5). Вероятность того, что случайная величина попадет в некоторый интервал, можно найти или с помощью функции плотности, или с помощью функции распределения. Рассмотрим оба варианта :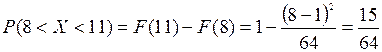 
; 
.
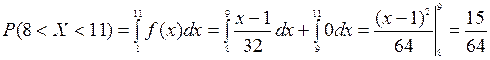Теоретические вопросы к разделу 5.
1. Функция плотности распределения вероятностей.
2. Числовые характеристики непрерывных случайных величин.
3. Функция распределения вероятностей непрерывной случайной величины.
4. Равномерное распределение .
5. Показательный закон распределения.
6. Нормальный закон распределения.
Задание к разделу 5.
Непрерывная случайная величина Х задана своей плотностью распределения вероятностей f(x). Требуется:
1) определить коэффициент А;
2) найти функцию распределения F(x);
3) схематично построить графики функций f(x) и F(x);
1) вычислить математическое ожидание, дисперсию и среднее
квадратическое отклонение случайной величины Х;
2) определить вероятность того, что Х примет значения из интервала
(a, b).
1. 
, 
.
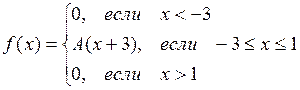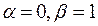2. 
, 
.
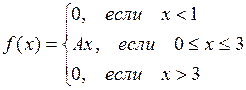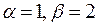3. 
, 
.
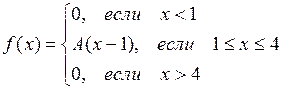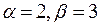4. 
, 
.
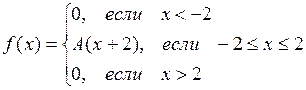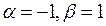5. 
, .
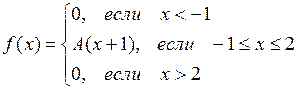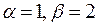6. 
, 
.
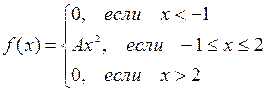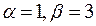7. 
, 
.
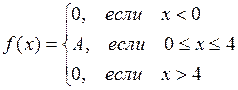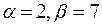8. 
, 
.
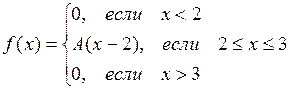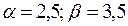9. 
, 
.
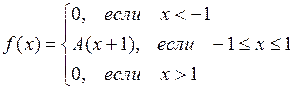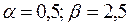10. 
, 
.
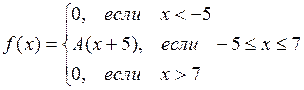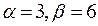КОНТРОЛЬНАЯ РАБОТА № 4
Теория вероятностей. Случайные события.
Случайные величины.
Методические указания и задания