Модели систем массового обслуживания

Содержание.

Введение ........................................................................................................................... 1

1 Модели систем массового обслуживания............................................................... 4

1.1 Предметная область теории телетрафика....................................................... 4

1.1.1 Информационные процессы и конфликты обслуживания......................... 4

1.1.2 Основные определения теории систем массового обслуживания............. 5

1.1.3 Модели потока требований............................................................................ 9

Нестационарный пуассоновский поток............................................................... 12

Примитивный поток.............................................................................................. 13

Поток с ограниченным последействием.............................................................. 13

Поток Эрланга........................................................................................................ 13

1.1.4 Поток освобождений серверов.................................................................... 14

1.2 Модели систем массового обслуживания..................................................... 15

1.2.1 Математическое введение в теорию цепей Маркова. (Markov’s chain ).. 15

Непрерывные цепи Маркова................................................................................. 18

1.2.2 Классификация систем массового обслуживания..................................... 22

1.2.3 Формула Литтла. (Little)............................................................................... 22

1.3 Анализ систем массового обслуживания с марковскими потоками требований. 24

1.3.1 Система М/M/1. Анализ................................................................................ 24

1.3.2 Cистема с конечным накопителем: M/M/1:N............................................. 27

1.3.3 Система с несколькими серверами: M/M/m................................................ 29

1.3.4 Система обслуживания с m серверами явными потерями: M/M/m/Loss. 32

1.3.5 Система обслуживания M/M/m:K/M конечное число источников нагрузки, m серверов и конечный накопитель................................................................................... 33

1.3.6 Система типа M/M/m:m................................................................................. 35

1.4 Вероятность занятия серверов....................................................................... 36

1.5 Сравнительные характеристики моделей Эрланга и Энгсета................... 36

1.6 Примеры анализа систем связи...................................................................... 38

1.7 Системы с неполнодоступным включением серверов............................... 39

1.8 Основы марковской теории сетей массового обслуживания..................... 47

1.8.1 Анализ систем массового обслуживания без явных потерь..................... 47

1.8.2 Анализ сетей массового обслуживания с блокировками. Метод вероятностных графов Ли. 52

2 Анализ и оптимизация коммутационных систем................................................ 54

3 Анализ систем с произвольным законом распределения времени обслуживания 60

4 Сравнение характеристик качества обслуживания в сетях с коммутацией каналов и коммутацией пакетов............................................................................................................ 64

4.1 Анализ времени доставки сообщений в сети с коммутацией каналов..... 64

4.2 Анализ времени доставки сообщений в сетях с коммутацией пакетов.... 70

5 Анализ характеристик каналов с интеграцией речи и данных.......................... 75

5.1 Метод производящих функций...................................................................... 75

5.2 Модели интеграции речи и данных.............................................................. 77

5.2.1 Интеграция на основе обслуживания в порядке поступления................ 77

5.2.2 Интеграция с абсолютным приоритетом.................................................... 81

5.2.3 Интеграция на основе стратегии подвижной границы........................... 84

6 Система типа G/G/1................................................................................................. 89

7 Анализ систем массового обслуживания с приоритетами................................. 95

7.1 Дисциплины обслуживания. Модель с приоритетами............................... 95

7.2 Основная модель расчета среднего времени ожидания.............................. 96

7.3 Дисциплины обслуживания с приоритетами, зависящими от времени. 101

7.4 Оптимизация назначения приоритетов...................................................... 104

Список используемой литературы.......................................................................... 108

Введение

В курсе «Теория телетрафика» рассматриваются процессы обработки информации в телекоммуникационных сетях с точки зрения теории систем массового обслуживания. Основными понятиями системы массового обслуживания (СМО) являются заявки (требования) и серверы, называемые также обслуживающими приборами. Заявки образуют входной поток на входе СМО и работа системы состоит в обслуживании этих заявок, затрачивая на каждую некоторое время. Если число серверов недостаточно для обслуживания всех поступивших заявок, то возникает конфликт, разрешение которого состоит в том, что часть заявок отбрасывается или помещается в очередь. Поэтому в зарубежной литературе, обычно используется термин Queuing Theory (теория очередей).

В телекоммуникационных системах заявка ассоциируется, прежде всего, с попыткой абонента получить доступ к ресурсам системы для передачи или приема сообщений. Например, снимая трубку телефонного аппарата, абонент телефонной сети порождает сигнал, который является заявкой на обслуживание его этой сетью. Если аппарат включен через блокиратор, и снявший трубку не услышит ничего – то сеть отказывает ему в обслуживании, заявка отбрасывается. Наличие гудка означает, что заявка принята и абонент получает обслуживание. Абонент телефонной сети порождает заявки и другого типа – набор номера вызываемого абонента. Эта заявка также может быть удовлетворена, если ресурсы сети позволят установить соединение между всеми телефонными станциями, которые обеспечивают передачу речевого сигнала от телефона вызывающего до телефона вызываемого абонента. Однако, это произойдет не всегда. Заявка на установление соединения может быть не удовлетворена. Вероятность такого события для абонентов телефонной сети рассматривается как характеристика качества обслуживания этой сети и расчет вероятности отказа в обслуживании является одной из важнейших задач теории телетрафика. Рассмотрим теперь пользователей другой, компьютерной сети, например Internet. Здесь качество сети ассоциируется с другой характеристикой – временем доступа к тому или иному ресурсу. Причиной замедления работы являются образующиеся в маршрутизаторах очереди, состоящие из пакетов, в которые упакована вся передающаяся по сети информация. В компьютерных сетях заявка на передачу информации от одного узла к другому даже в случае нехватки ресурса, как правило, не отбрасывается, а помещается в очередь на ожидание освобождения необходимого ресурса. Поэтому характеристикой качества обслуживания в этом случае считают время нахождения заявки в очереди на обслуживание. Задача расчета времени ожидания также решается в теории телетрафика.

Таким образом, изучив основные методы теории телетрафика, вы сможете рассчитать характеристики качества обслуживания в телекоммуникационных системах, управлять основными параметрами качества обслуживания реальных сетей и систем и измерять их, а также предложить оптимальные с точки зрения качества обслуживания технические решения при проектировании новых сетей и систем. Вопросы построения сетей с гарантированным качеством услуг являются предметом внимания ITU-International Telecommunication Union (Международного Союза Электросвязи) особенно в связи с развертывание работ по созданию глобальных сетей третьего и четвертого поколений в третьем тысячелетии.

ITU выделяет Traffic Engineering в явном и неявном виде как одно из важнейших направлений деятельности специалистов по телекоммуникациям и посвящает ему целый ряд рекомендаций, определения и методики из которых будут использованы далее в настоящем пособии. В этом отношении наш взгляд на теорию телетрафика не всегда совпадает с классическим изложением, принятым в отечественной литературе. В прекрасном учебнике по теории телетрафика [1] вы найдете при необходимости терминологию и подходы к решению задач, относящихся к классической телефонии.

Изложенный ниже курс лекций был впервые прочитан автором для студентов специальности «Сети связи и системы коммутации» Нижегородского государственного технического университета в 1998/1999 учебном году. С текстом лекций были ознакомлены многие преподаватели и специалисты. Всем им автор выражает глубокую благодарность. Особенно признателен автор профессорам МТУСИ А.П.Пшеничникову и Ю.В. Лазареву, доцентам НГТУ А.Б. Зуеву и А.А. Кочеткову за ценные замечания, существенно способствующие улучшению рукописи. Автор благодарит также всех своих студентов, кому пришлось воспринимать изложенный курс на слух и внесших вклад в появление его письменной реализации.

Эрл

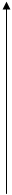120

Час

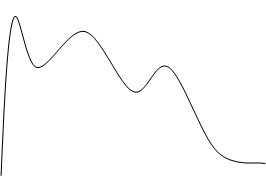
Рис.1.2. Результаты измерения интенсивности нагрузки на нескольких городских АТС.

В американской литературе вы можете встретить и другую единицу измерения интенсивности нагрузки, называемую CCS – Centrum (or hundred) calls second (гектосекундозанятия). Это число отражает работу серверов в сто секундных единиц измерения в течение часа.

Вы всегда можете пересчитать CCS в Эрланги по формуле

36 CCS=1 Эрланга

Всюду выше мы говорили о реально измеренной нагрузке, которая соответствует совершенной СМО работе. Такая нагрузка называется обычно обслуженной нагрузкой. Если часть поступивших требований не была обслужена системой ввиду перегрузки серверов, то можно ввести понятия потенциальнойнагрузки и поступающей нагрузки. Потенциальная нагрузка – это гипотетическая обслуженная СМО нагрузка в предположении, что все требования были обслужены. Поступающая нагрузка определяется как произведение среднего числа поступающих требований в единицу времени на среднее время одного обслуживания. Разность между потенциальной и обслуженной нагрузкой называют потерянной, а разность между поступающей и обслуженной – избыточной нагрузкой.

Ненулевое значение потерянной или избыточной нагрузки говорит о ненулевой вероятности блокировки или пропуска требований или ненулевом значении задержки требований во входной очереди. Как было уже отмечено выше, значения вероятности блокировки или пропуска, а также параметры функции распределения задержки, чаще всего среднее значение задержки, определяют так называемые показатели качества обслуживания (QoS-Quality of Service).

Важными характеристиками системы массового обслуживания являются ее производительность и пропускная способность.

Пропускная способность системы - это интенсивность обслуженной нагрузки при заданном качестве обслуживания.

Производительность системы - это предельное, статистически усредненное число обслуживаний в единицу времени при заданном качестве обслуживания.

1.1.3 Модели потока требований

Поступающие на вход системы массового обслуживания требования (заявки, запросы) образуют поток дискретных событий, полностью определяемый множеством моментов времени их поступления 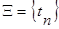. Для детерминированного потока значения t_n задаются таблицей или формулой. На практике этот поток случайный и значения моментов поступления запросов есть значения случайной величины, задаваемой функциями распределения вероятности t_n либо интервала между поступлениями Dt : .

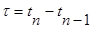В зависимости от вида функции распределения вероятности потоки требований наделяют соответствующими названиями. В общем случае случайные потоки можно классифицировать по наличию или отсутствию трех основных свойств: стационарности, последействия и ординарности.

Стационарность - независимость вероятностных характеристик от времени. Так вероятность поступления определенного числа требований в интервал времени длиной t для стационарных потоков не зависит от выбора начала его измерения.

Последействие - вероятность поступления требований в интервале (t₁ , t₂) зависит от событий, произошедших до момента t₁.

Ординарность - вероятность поступления двух и более требований за бесконечно малый интервал времени Δt есть величина бесконечно малая более высокого порядка, чем Δt.

К основным характеристикам случайных потоков относят ведущую функцию, параметр потока и интенсивность потока.

Ведущей функцией потока 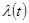называют математическое ожидание числа требований в промежутке времени (0,t).

Параметр потока вместе с интенсивностью потока являются важнейшими характеристиками темпа поступления требований. Это плотность вероятности поступления требований в момент времени t и характеризуется тем, что вероятность поступления хотя бы одного требования в бесконечно малом промежутке времени пропорциональна с точностью до бесконечно малой более высокого порядка длине этого промежутка. 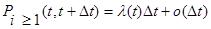. Откуда:

.

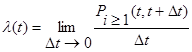Для стационарного потока параметр потока постоянный и равен:

.

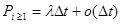Интенсивность потока учитывает возможную неординарность потока, т.е. одновременно поступающие требования и определяется как математическое ожидание числа вызовов в единицу времени в данный момент. Для ординарных потоков интенсивность потока и есть его параметр.

Пуассоновский (простейший) поток запросов

Стационарный ординарный поток без последействия называют простейшим. Он задается набором вероятностей P_i(t) поступления i требований в промежутке длиной t.

Можно показать, что при этих предположениях формула для P_i(t) дается формулой Пуассона (Poisson):

.

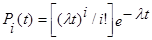Проанализируем основные характеристики пуассоновского потока. Рассмотрим отношение P_i(t)/P_i-1(t). При i ≤ λt вероятность растет, а при обратном соотношении – убывает. Графики функции распределения Пуассона в зависимости от величины λt для различных значений k приведены на рис. 1.3.

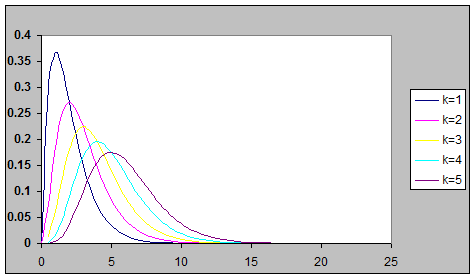
Рис. 1.3. Графики Пуассоновского распределения в зависимости от lt для различных k.

Наряду с распределением P_i(t) используют вероятности поступления не менее i требований в интервал t или не более i требований за время t:

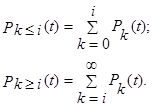
Если рассмотреть закон распределения вероятностей промежутка между поступлением соседних требований τ, то можно показать, что

.

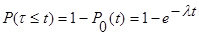Дифференцируя, получаем плотность распределения вероятностей: .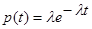

Случайная величина с такой плотностью вероятностей называется экспоненциально - распределенной (с показательным распределением). Математическое ожидание экспоненциально распределенной случайной величины равно

,

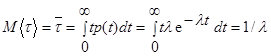а дисперсия и среднеквадратическое отклонение соответственно будут равны:

,

.

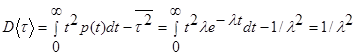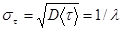Определим математическое ожидание и дисперсию числа требований за промежуток t :

,

.

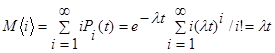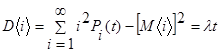Одним из важных свойств пуассоновского потока является аддитивность.

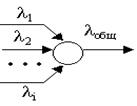Если образовать поток заявок как объединенный из нескольких пуассоновских потоков, то его суммарная интенсивность будет равна сумме интенсивностей каждого отдельного потока _.

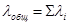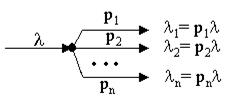При разъединении пуассоновского потока на несколько потоков так, что каждое требование исходного потока с вероятностью p_i (Sp_i =1) поступает на i-тоенаправление, поток i направления будет также пуассоновским с интенсивностью lp _i.

Примитивный поток.

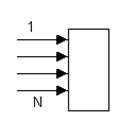
Это ординарный поток, параметр которого прямо пропорциона­лен числу свободных источников N_i =(N-i). Здесь N – общее число источников требований, i- число обслуживаемых в данный момент источников. Для примитивного потока параметр потока определяется как λ_i=αN_i=α(N-i) с некоторым коэффициентом α. Среднее значе­ние параметра примитивного потока: 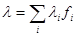, где f_­i - вероятность того, что об­служивается i источников. Средняя интенсивность потока заявок от одного источника: .

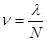Поток Эрланга

Частный случай и получается “просеиванием” потока Пальма. Если отбрасывать каждую вторую заявку – то получается поток Эрланга второго порядка, если каждую третью – третьего порядка и т.д.

Простейший пуассоновский поток можно рассматривать как поток Эрланга первого порядка. Обозначим p_n(t) плотность вероятности промежутка между заявками. Можно получить что: .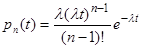

Закон распределения для потока Эрланга n-го порядка:

,

.

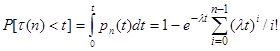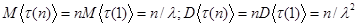Нормируем масштаб времени так, чтобы параметр потока не зависел от n .

Τ_н (n)=τ(n)/n ; интенсивность Λ_n

Нормированный поток Эрланга n – го порядка:

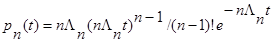
Обобщенный поток Эрланга n –го порядка .

Если τ(n) есть сумма случайных величин, каждая из которых распределена по показательному закону с параметром λ_i

,

,

, .

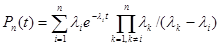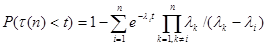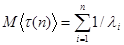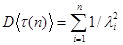Теорема 1.

Состояния неприводимой цепи Маркова либо все невозвратные, либо все возвратные нулевые, либо все возвратные ненулевые. В случае периодической цепи все состояния имеют один и тот же период.

Вторая теорема рассматривает вероятности достижения состояний в стационарном (то есть не зависящем от начального распределения вероятностей) режиме. Соответствующее распределение вероятностей также называют стационарным. Нахождение стационарного распределения вероятностей достижения состояний одна из основных задач теории телетрафика.

Теорема 2.

Для неприводимой и апериодической цепи Маркова всегда существуют предельные вероятности, не зависящие от начального распределения вероятностей. Более того, имеет место одна из следующих двух возможностей:

А) все состояния цепи невозвратные или все возвратные нулевые, и тогда все предельные вероятности равны нулю и стационарного состояния не существует;

Б) все состояния возвратные ненулевые и тогда существует стационарное распределение вероятностей:

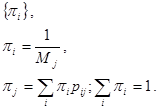
Состояние называется эргодическим, если оно апериодично и возвратно ненулевое. Если все состояния цепи Маркова эргодичны, то вся цепь называется эргодической. Предельные вероятности эргодической цепи Маркова называют вероятностями состояния равновесия, имея в виду, что зависимость от начального распределения вероятностей полностью отсутствует.

Цепь Маркова с конечным числом состояний (конечная цепь), удобно изображать в виде ориентированного графа, называемого диаграммой переходов (рис.1.5). Вершины графа ассоциируются с состояниями, а ребра с вероятностями переходов.

Вычисления вероятностей достижения состояний производится прямыми методами или с помощью z-преобразования.

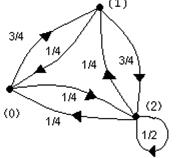
Рис. 1.5 Цепь Маркова.

Введем матрицу вероятностей переходов и вектор-строку вероятностей на шаге n

.

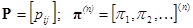Распределение вероятностей на произвольном шаге тогда будет подчиняться матричному соотношению:

.

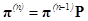Оно позволяет рекуррентно вычислять все вероятности состояний. Для нахождения предельного распределения (стационарного) нужно решить уравнение:

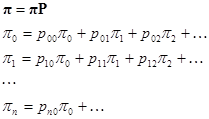
Его можно решать как систему линейных алгебраических уравнений, если цепь конечна.

Для примера, показанного на рис.1.5, имеем:

.

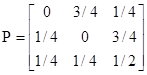и решение матричного уравнения сводится к решению системы трёх уравнений:

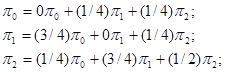
Коэффициенты первого уравнения в этой системе дополняют до единицы сумму коэффициентов второго и третьего уравнений; это свидетельствует о линейной зависимости между ними. Поэтому для решения системы уравнений нужно ввести дополнительное нормирующее условие. В данном примере: .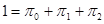

Решая систему полученных уравнений, имеем:

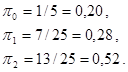
Уравнение для вероятности достижения состояния в переходном режиме решить значительно труднее. Некоторого упрощения можно достигнуть, используя z – преобразование. Применим его к уравнению для переходных вероятностей

.

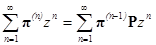Обозначая соответствующие преобразования, получим: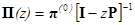

Все полученные здесь математические результаты относились к однородным Марковским процессам, где вероятности переходов не зависят от времени. В более общем случае такая зависимость имеет место.

Рассмотрим вероятности перехода системы из состояния i на m-том шаге в состояние j на n-том шаге для n > m.

Можно показать, что эти вероятности связаны между собой, так называемым уравнениями Чепмена-Колмогорова.(Chapman - Kolmogorov)

.

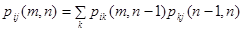Для однородных цепей Маркова эти уравнения упрощаются так как

.

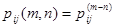И сводятся к анализируемым выше.

Непрерывные цепи Маркова.

Случайный процесс X(t) с дискретным множеством значений образует непрерывную цепь Маркова, если

.

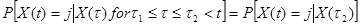Будущие состояния зависят от прошлого только через текущее состояние. Для непрерывный цепей Маркова основным также является уравнение Чепмена –Колмогорова, для однородной цепи имеющее вид: .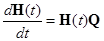

Здесь матрица H(t)= [ p_ij(t)] - матрица вероятностей перехода из состояния i в состояние j в момент времени t , а матрица Q называется матрицей интенсивностей переходов. Ее элементы имеют следующий смысл: если в момент времени t система находилась в состоянии E_i , то вероятность перехода в течение промежутка времени (t,t+Δt) в произвольное состояние E_j задается величиной q_ij(t)Δt + o(Δt), а вероятность ухода из состояния E_i величиной -q_iiΔt + o(Δt).

Таким образом, интенсивности переходов можно вычислять как соответствующие пределы при стремлении к нулю длительности временного интервала.

Наиболее важным для дальнейшего использования является класс непрерывных цепей Маркова называемых «процессами гибели - размножения»(Birth – death process). Для таких систем из состояния k возможны переходы только в состояния k, k-1 и k+1 в следующие моменты времени:

· в момент t объем популяции был равен k и в течение времени (t,t+Δt) не произошло изменения состояния

· в момент t объем популяции был равен k-1 и в течение времени (t,t+Δt) родился один член популяции

· в момент времени t объем популяции был равен k+1 и в течение времени (t,t+Δt) погиб один член популяции

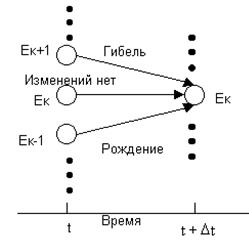
Рис. 1.6. Возможные переходы в состояние Ек.

Будем искать вероятность того, что в момент времени t объем популяции равен k , обозначив его P_k(t). Можно записать соотношения для вероятности достижения со­стояния k в момент времени t+Δt:

.

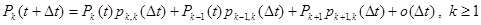Определим граничные и нормирующие условия:

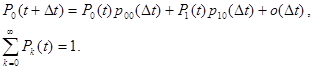
Выразим вероятности переходов за интервал Δt через интенсивности

Вер(+1)=λ_kΔt+o(Δt) ; Вер(-1)=μ_kΔt+o(Δt).

Вероятность нуля рождений 1- λ_kΔt+o(Δt) , а нуля гибелей 1- μ_kΔt+o(Δt).

Таким образом, вероятность того, что состояние k сохранится неизменным, будет равно произведению [1- λ_kΔt+o(Δt)][ 1- μ_kΔt+o(Δt)].

Тогда уравнения Чепмена-Колмогорова приобретают вид

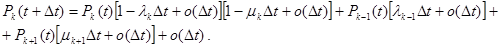
Раскрывая скобки и проводя деление на Δt, получим:

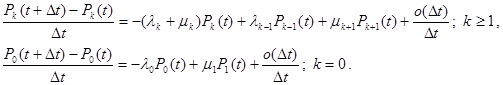
В пределе получается система дифференциально-разностных уравнений, решение которой будут играть важную роль для практических задач.

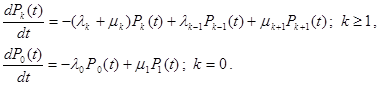
В соответствие этой системе уравнений можно поставить наглядную диаграмму интенсивностей переходов, которая аналогична диаграмме переходов для дискретных цепей Маркова (Рис 1.7.)

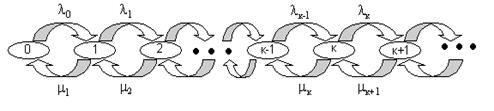
Рис.1.7. Диаграмма интенсивностей переходов для процесса размножения и гибели.

Овалам здесь соответствуют дискретные состояния, а стрелки определяют интенсивности потоков вероятности (а не вероятности!) переходов от одного состояния к другому.

Имеет место своеобразный «закон сохранения»:

Разность между суммой интенсивностей, с которой система попадает в состояние k и суммой интенсивностей, с которой система покидает это состояние должна равняться интенсивности изменения потока в это состояние (производной по времени).

Применение закона сохранения позволяет получать уравнения для любой подсистемы Марковской цепи типа процесса «гибели-размножения». Особенно эффективным оказывается построение решений в стационарном, установившемся режиме, когда можно полагать что вероятности в произвольный, достаточно отдаленный момент времени, остаются постоянными.

Приравнивая производную по времени нулю, получаем систему разностных уравнений

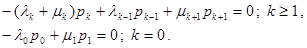
Полагая, что интенсивности λ_-1 =λ_-2 = λ_-3 =…0; μ₀ = μ_-1 = μ_-2 = μ_-3 =…=0, второе уравнение выписывать отдельно далее не потребуется. Итак, стационарный режим в цепи Маркова будет описываться системой разностных уравнений и условием нормировки для вероятностей

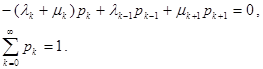
Нетрудно видеть, что эти уравнения легко выводятся из закона сохранения интенсивностей вероятностей. В стационарном режиме разность потоков равна нулю и полученные выше уравнения приобретают смысл уравнений равновесия или баланса, как их и называют.

.

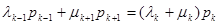Интенсивность потока вероятностей в состояние k равна интенсивности потока из этого состояния.

Решать уравнение баланса можно, сначала определив при k =0 значение

.

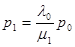Затем, построив систему уравнений для k =1, можно получить .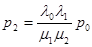

Далее получаем

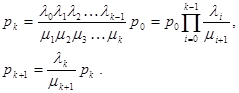
Из условия нормировки: .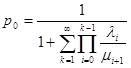

Система, описываемая полученными выше выражениями, будет иметь стационарные вероятности состояний, когда она эргодическая. Это условие может быть выражено через соотношение интенсивностей. Необходимо и достаточно, чтобы существовало некоторое значение k , начиная с которого выполнялось неравенство

.

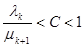Для большинства реальных систем массового обслуживания это неравенство выполняется.

A/b/c :d/e/f

a –распределение поступающего потока запросов.

b– закон распределения времени обслуживания.

Типовые условные обозначения:

М – экспоненциальное (Марковское) распределение,

D – детерминированное распределение,

E^k – эрланговское распределение k-го порядка,

HM^k – гиперэкспоненциальное,

HE^k – гиперэрланговское распределение порядка k,

GI – произвольное распределение независимых промежутков между заявками,

G – произвольное распределение длительностей обслуживания.

c –структура системы обслуживания (обычно число серверов).

d –дисциплина обслуживания (параметры после двоеточия иногда опускают).

Обычно используется сокращенное символическое обозначение, например FF вместо FIFO, LF, PR и т.п.

e –максимальное число запросов, воспринимаемое системой, может употребляться символ ¥.

f –максимальное число запросов к системе обслуживания.

В некоторых публикациях последними символами отражают качественные характеристики системы обслуживания. Некоторые общие результаты и основы математического аппарата, необходимого для анализа можно получить, рассматривая системы G/G/m.

Формула Литтла (Little).

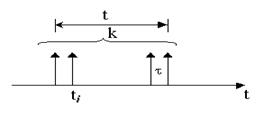
Рассмотрим временную диаграмму работы системы массового обслуживания (рис. 1.8), отразив на ней последовательность поступления требований, помещение требований в очередь и обработки серверами системы.

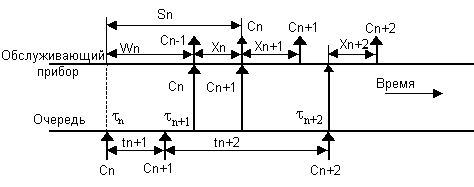
Рис. 1.8 Временная диаграмма работы системы массового обслуживания.

В общем случае ясно, что с увеличением числа требований растет время ожидания. Установим соотношение между средним числом требований в системе, интенсивностью потока и среднего времени пребывания в системе. Обозначим число поступающих в промежутке времени (0 , t) требований как функцию времени α(t).

Число исходящих из системы заявок (обслуженных) на этом интервале обозначим δ(t). На рисунке 1.9 показаны примеры функциональных зависимостей этих двух случайных процессов от времени.

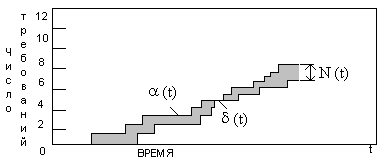
Рис. 1.9 Зависимость между средним числом требований в системе, интенсивностью потока и средним времени пребывания в системе.

Число требований, находящихся в системе в момент t будет равно:

.

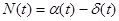Площадь между двумя рассматриваемыми кривыми от 0 до t - дает общее время, проведенное всеми заявками в системе за время t.

Обозначим эту накопленную величину γ(t) . Если интенсивность входного потока равна λ, а средняя интенсивность за время t: 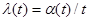,то время, проведенное одной заявкой в системе, усредненное по всем заявкам будет равно:

.

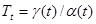Наконец, определим среднее число требований в системе в промежутке (0,t):

.

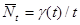Из последних трех уравнений следует, что: 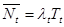, (где ).

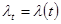Если в СМО существует стационарный режим, то при t→ ∞ , будут иметь место соотношения:

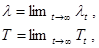
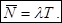
Последнее соотношение означает, что среднее число заявок в системе равно произведению интенсивности поступления требований в систему на среднее время пребывания в системе. При этом не накладывается никаких ограничений на распределения входного потока и времени обслуживания. Впервые доказательство этого факта дал Дж.Литтл и это соотношение носит название формула Литтла.

Интересно, что в качестве СМО можно рассмотреть только очередь из заявок в буфере. Тогда формула Литтла приобретает иной смысл - средняя длина очереди равна произведению интенсивности входного потока заявок на среднее время ожидания в очереди: .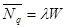

Если наоборот рассматривать СМО только как серверы, то формула Литтла дает:

,

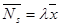где 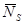– среднее число заявок в серверах, а 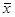– среднее время обработки в сервере.

В любом случае: .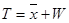

Одним из основных параметров, которые используются при описании СМО, является коэффициент использования (utilization factor). Это фундаментальный параметр, так как он определяется как отношение интенсивности входного потока к пропускной способности системы. Поскольку пропускная способность СМО содержащей m серверов может быть определена как: 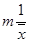, то коэффициент использования может быть определен как:

.

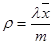Нетрудно видеть, что коэффициент использования равен в точности интенсивности нагрузки, если СМО с одним сервером и в m раз меньше для систем с m серверами. Величина коэффициента использования равна среднему значению от доли занятых серверов и .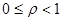

Если в СМО типа G/G/1 существует стационарный режим и можно определить вероятность того, что в некоторый случайный момент сервер будет свободный, то

.

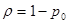Чтобы рассмотреть более тонкие результаты теории телетрафика нам понадобится ряд математических моделей.

Теперь перейдем к рассмотрению самой простой из задач анализа СМО – рассмотрим систему типа M/M/1.

1.3 Анализ систем массового обслуживания с марковскими потоками требований.

В этом разделе вы познакомитесь с методами расчета характеристик качества обслуживания QоS систем массового обслуживания, если они могут быть описаны моделью с марковским потоком требований на входе, т.е. интервалы времени между поступлениями соседних требований являются случайной величиной с экспоненциальным распределением.

Система М/M/1. Анализ.

Как было описано при классификации систем, это система с пуассоновским входным потоком заявок, экспоненциальным законом распределения времени обслуживания и одним сервером.

На рис. 1.10 приведена простейшая схема такой системы. Она содержит буфер, который может хранить очередь бесконечной длины, состояние которой может быть отождествлено с числом заявок, содержащихся в очереди в каждый момент времени.

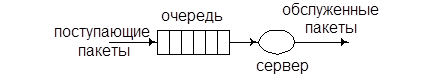
Рис. 1.10 СМО типа М/М/