Тема 2.1. Математическое ожидание и дисперсия случайной величины.

Под случайным событием, связанным с некоторым опытом понимается всякое событие, которое при осуществлении этого опыта либо происходит, либо не происходит.

Классическое определение вероятности: 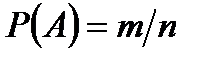вероятностью события 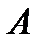называется отношение числа исходов 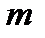, благоприятствующих наступлению данного события 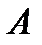, к числу 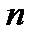всех исходов несовместных.

Невозможное событие 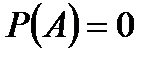; Достоверное событие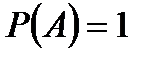

Основные теоремы теории вероятностей и их следствия:

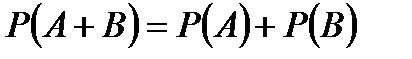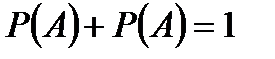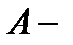Т.1: ; Следствие: где противоположное событие

Т.2: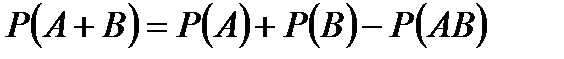

Вероятность наступления события 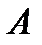, вычисленная в предположении, что событие 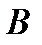уже произошло, называется условной вероятностью события 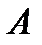при условии 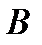и обозначается: 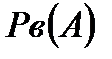или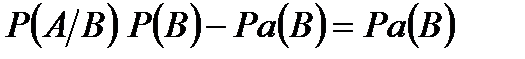

Формула полной вероятности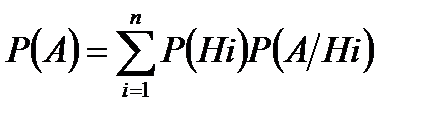

Вероятность совместного появления независимых событий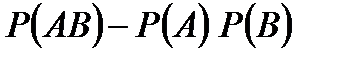

Вероятность совместного появления зависимых событий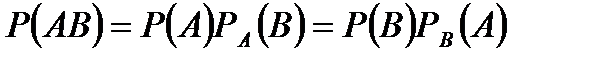

Формула полной вероятности

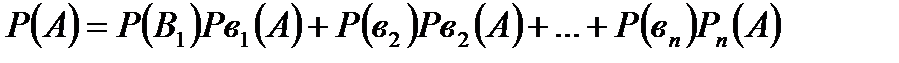где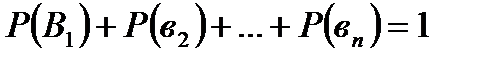

Формула Байеса: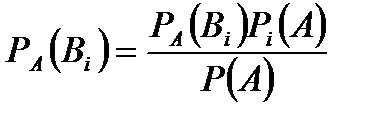

Где 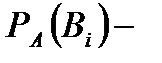вероятность каждой из гипотез после испытания, в результате которого наступило событие А;

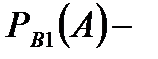условная вероятность события А после наступления события ;

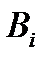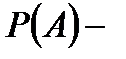находится по формуле полной вероятности

Формула Бернулли: ,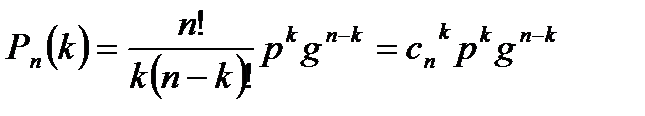

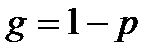
Определение: случайной величиной называется функция, заданная на множестве исходов данного опыта.

Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа, которая эта величина принимает с определенными вероятностями.

Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей. 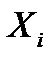, а вторая – вероятности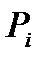

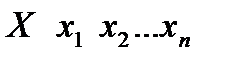
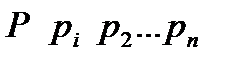где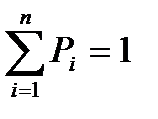

Характеристикой среднего значения случайной величины служит математическое ожидание.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений и их вероятности:

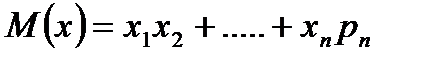
Свойства:

1)

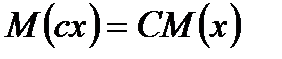
2)

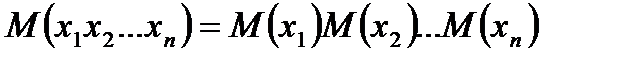
3)

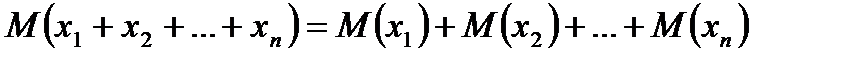
Математическое ожидание биноминального распределения равно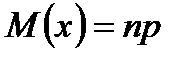

Характеристики рассеяния возможных значений случайной величины вокруг математического ожидания – дисперсия, среднее квадратичное отклонение. Дисперсия случайной величины: 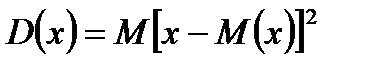или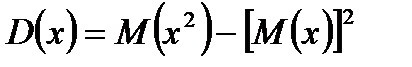

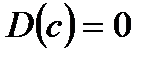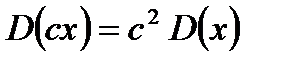Свойства: 1) ; 2) ; 3)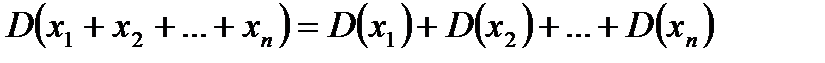

Дисперсия биноминального распределения:npq

Средним квадратичным отклонением случайной величины называют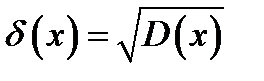

Задача: Найти математическое ожидание дискретной случайной величины Х, заданной законом распределения:

Х -4 6 10

Р 0,2 0,3 0,5

Решение:

Найти математическое ожидание равно сумме произведений всех возможных значений Х на их вероятности.

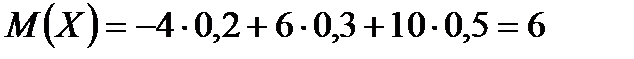
Задача: Случайные величины X и Y независимы. Найти дисперсию случайной величины 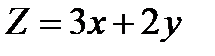, если известно, что .

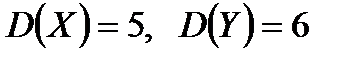Решение:

Так как величины X и Y независимы, то независимы также и величины 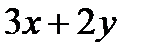. Используя свойства дисперсии 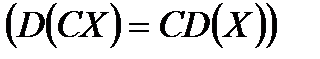, получим:

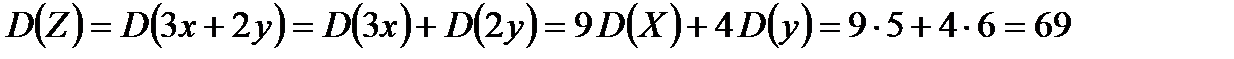
Задача: Найти дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения:

Х -5 2 3 4

Р 0,4 0,3 0,1 0,2

Дисперсию можно вычислить исходя из ее определения, но мы воспользуемся формулой: 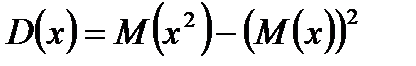, которая быстрее ведет к цели. Найдем математическое ожидание Х: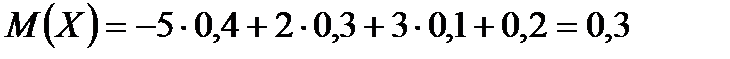

Напишем закон распределения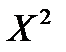

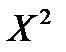25 4 9 16

Р 0,4 0.3 0,1 0,2

Найдем математическое ожидание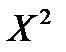

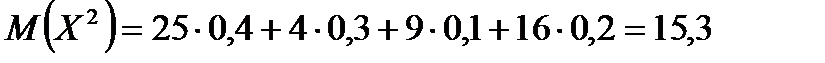
Найдем искомую дисперсию: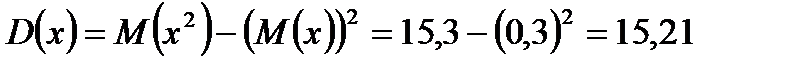

Найдем искомое среднее квадратичное отклонение

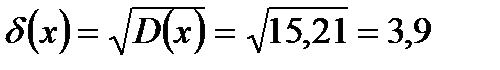
Вопросы для самопроверки:

1. Что служит характеристикой среднего значения случайной величины?

2. Что называется математическим ожиданием случайной величины?

3. Перечислить свойства математического ожидания.

4. Чему равно математическое ожидание биноминального распределения?

5.Что является характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания?

6.Что называется дисперсией случайной величины?

7. Свойства дисперсии?

8.Чему равна дисперсия биноминального распределения?

9. Что называют квадратичным отклонением?

10.Чему равно среднее квадратичное отклонение случайной величины?