Математическое ожидание и дисперсия непрерывной случайной величины.

1) Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на вероятности этих значений.

В теории вероятности и во многих ее приложениях большое значение имеют различные числовые характеристики случайных величин. Основными из них являются математическое ожидание и дисперсия.

1. Математическое ожидание случайной величины и его свойства.

Рассмотрим сначала следующий пример. Пусть на завод поступила партия, состоящая из N подшипников. При этом:

m1 - число подшипников с внешним диаметром х1,

m2 - число подшипников с внешним диаметром х2,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

mn - число подшипников с внешним диаметром хn,

Здесь m1+m2+...+mn=N. Найдем среднее арифметическое значение xср внешнего диаметра подшипника. Очевидно,

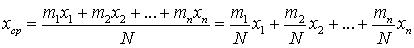
Внешний диаметр вынутого наудачу подшипника можно рассматривать как случайную величину 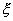, принимающую значения х1, х2, ..., хn, c соответствующими вероятностями p1=m1/N, p2=m2/N, ..., pn=mn/N, так как вероятность pi появления подшипника с внешним диаметром xi равна mi /N. Таким образом, среднее арифметическое значение xср внешнего диаметра подшипника можно определить с помощью соотношения

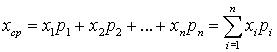
Пусть 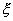- дискретная случайная величина с заданным законом распределения вероятностей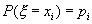

Значения х1 х2 . . . хn

Вероятности p1 p2 . . . pn

Математическим ожиданием 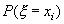дискретной случайной величины 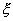называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е. *

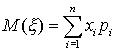(39)

Возвращаясь к разобранному выше примеру, мы видим, что средний диаметр подшипника равен математическому ожиданию случайной величины 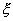- диаметру подшипника.

Математическим ожиданием 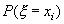непрерывной случайной величины 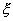с плотностью распределения 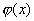называется число, определяемое равенством

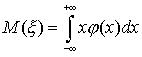(40)

Интеграл должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)

При этом предпологается, что несобственный интеграл, стоящий в правой части равенства (40) существует.

Рассмотрим свойства математического ожидания. При этом ограничимся доказательством только первых двух свойств, которое проведем для дискретных случайных величин.

1°. Математическое ожидание постоянной С равно этой постоянной.

Доказательство. Постоянную C можно рассматривать как случайную величину 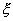, которая может принимать только одно значение C c вероятностью равной единице. Поэтому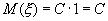

2°. Постоянный множитель можно выносить за знак математического ожидания, т.е.

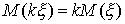
Доказательство. Используя соотношение (39), имеем

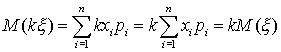
3°. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:

(41)

4°. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин **:

(42)

Дальше...

* в случае, если множество возможных значений дискретной случайной величины образует бесконечную последовательность x1, x2, ..., xn, ..., то математическое ожидание этой случайной величины определяется как сумма ряда

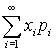
причем требуется, чтобы этот ряд абсолютно сходился.

** Под суммой (произведением) двух случайных величин и понимают случайную величину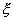

и 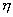понимают случайную величину

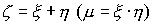
, возможные значения которой состоят из сумм (произведений) каждого возможного значения величины 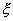и каждого возможного значения величины .

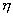2) Дисперсией непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называется определенный интеграл

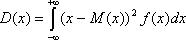
или

.

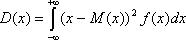
При вычислении дисперсии НСВХ также можно пользоваться формулой

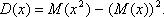
Вопрос 15

Числовые характеристики случайной величины: центральные и начальные моменты, среднее квадратическое
отклонение, мода и медиана, асимметрия и эксцесс, квантиль, процентная точка.

Начальный момент к-го порядка случайной величины Х есть математическое ожидание к-ой степени этой случайной величины:

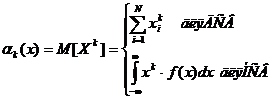
При К=0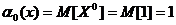

К=1 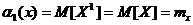- математическое ожидание;

К=2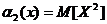

Центрированной случайной величиной 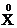называется случайная величина, математическое ожидание которой находится в начале координат(в центре числовой оси), т.е М[ 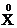]=0

Операция центрирования(переход от нецентрированной величины Х к центрированной )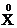

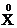=Х – m_x

Центральный момент порядка k случайной величины X есть математическое ожидние k-й степени центрированой случайной величины :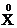

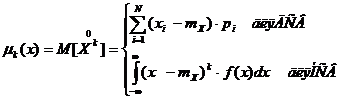
При К=0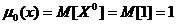

К=1 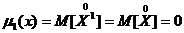- математическое ожидание;

К=2 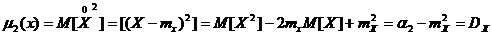-дисперсия.

Среднее квадратическое отклонениеслучайной величины Х характеризует ширину диапазона значений Х и равно:

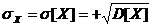
СКО измеряются в тех же физических единицах, что и случайная величины.

Правило 3 .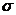

[ ]

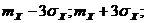Математическое ожидание и дисперсия (или СКО)- наиболее часто применяемые характеристики случайной величины. Они характеризуют наиболее важные черты распределения: его положение и степень разбросанности значений. Для более подробного описания используются начальные и центральные моменты высших порядков. Кроме математического ожидания на практике часто применяются и другие характеристики положения распределения значений.

Модаслучайной величины равна ее наиболее вероятному значению, т.е. то значение, для которого вероятность p_i (для дискретной случайной величины) или F(x) (для непрерывных случайных величины) достигает максимума:

F(x=max), p(X=M₀)= max

Распределение с одним максимумом плотности распределения называется «универсальным». Если многоугольник распределения или кривая распределения имеют более одного максимума, распределение называют «полимодальным». Если распределение обладает не максимумом, а минимумом, то оно называется «антимодальным».

Медианаслучайной величины Х равна такому ее значению, для которого выполняется условие p{X<Me}=p{X 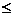Me}. Медиана , как правило, существует только для непрерывных случайных величин. Значение Me может быть определено как решение одного из следующих

Уравнений:

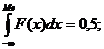
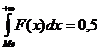
F(Me)= 0,5

В точке Me площадь, ограниченная кривой распределения, делится пополам.

Квантиль 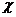_pслучайной величины Х- это такое ее значение, для которого выполняется условие

P{X<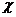 _p }=F( 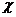_p )=p

Очевидно, что медиана – это квантиль _0,5.