Классификация задач оптимизации.

КУРС ЛЕКЦИЙ

по дисциплине «Методы оптимизации»

для студентов заочной формы обучения

по направлению 230201

«Информационные системы и технологии»

Воронеж 2013

Формализация задач определения оптимальных вариантов.

Под оптимизацией будем понимать процедуру определения в соответствии с установленными критериями наилучшего (оптимального) варианта из множества допустимых.

При этом объектами оптимизации могут быть различные технические и механические конструкции, системы, технологические и производственные процессы, информационные потоки, грузопотоки, маршруты.

Будем в дальнейшем называть их просто объектами, оптимальный вариант которых необходимо определить.

Каждый объект характеризуется набором параметров. При этом различают внешние, внутренние и выходные параметры.

Выходные параметры – величины, характеризующие свойства объекта и определяющие степень выполнения им своего функционального назначения (мощность, коэффициент усиления).

Внешние параметры - величины, характеризующие свойства внешней по отношению к объекту среды и оказывающие влияние на его функционирование (температура окружающей среды, параметры входных сигналов, напряжение источников питания).

Внутренние параметры - величины, характеризующие свойства отдельных элементов проектируемого объекта.

Совокупность внутренних и внешних параметров называется входными параметрами объекта.

Например, для вычислительной системы выходные параметры – производительность системы, коэффициенты нагрузки оборудования, вероятность решения поступающих задач и т. д.; внутренние параметры – емкость ЗУ, быстродействие процессоров; внешние параметры – интенсивность поступления задач и т. д.

Входные параметры делятся на управляемые (варьируемые) и неуправляемые. Варьируемые параметры в процессе оптимизации изменяются, вызывая, в свою очередь, изменение выходных параметров. В дальнейшем мы будем говорить только о варьируемых параметрах объекта. Обозначим их:

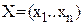
Т.е., X – это вектор варьируемых параметров. Они могут иметь различную физическую интерпретацию.

Различают задачи структурной и параметрической оптимизации.

Структурная оптимизация связана с определением оптимальной структуры объекта (т. е. перечень входящих в него элементов и способов их взаимосвязи между собой).

При параметрической оптимизации определяется значение параметров объекта заданной структуры, при которых достигается наилучшее сочетание его свойств.

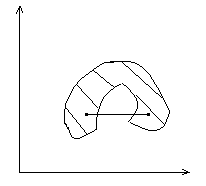
В общем виде задача оптимизации записывается следующим образом:

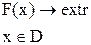
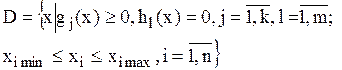(1)

Здесь X = (x₁, …x_n) – вектор варьируемых параметров объекта; F(x) – целевая функция – функция, характеризующая важные и существенные свойства объекта и являющаяся критерием оценки качества каждого из вариантов. Ее еще называют критерием оптимальности, критерием эффективности, показателем качества объекта и т. д. На основании вычисления F(x) анализируются и сравниваются между собой различные варианты объектов.

В процессе оптимизации объект должен удовлетворять различным требованиям (конструктивным, техническим, экономическим и т. д.), которые формализуются в виде системы ограничений.

Ограничения на варьируемые параметры вида x_imin £ x_i £ x_imax называют прямыми ограничениями. Здесь x_imin и x_imax верхние и нижние допустимые значения для i-го управляемого параметра.(так, например, если x_i – количество товара, то x_i ³ 0 и т. д.)

Ограничения вида g_i (x) ³ 0, h_l (x) = 0 – называют функциональными ограничениями и являются какими-либо функциями от входных параметров.

Совокупность функциональных и прямых ограничений образуют допустимую область D или область допустимых решений и значения варьируемых параметров должны принадлежать допустимой области.

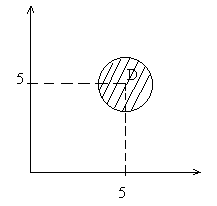
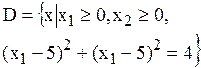
Область допустимых решений называется выпуклой, если для любой пары точек ÎD отрезок прямой линии, соединяет эти точки, тоже полностью Î D.

В противном случае - область невыпуклая.

Таким образом, решение задачи оптимизации сводится к определению значений управляемых параметров x₁ … x_n ,обеспечивающих экстремум (max или min) целевой функции F(x) и удовлетворяющих системе ограничений. Такой вектор X называется оптимальным решением. Задачи определения экстремальных значений параметров на допустимом множестве параметров носят еще название задач математического программирования.

Пример.

Для приведенной выше вычислительной системы оптимизационная задача может быть сформулирована следующим образом:

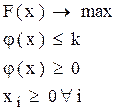
где F(x) – производительность системы

x_i – интенсивность поступления i-го типа задач

j(x) – средняя длина очереди

Необходимо определить интивности поступления каждого типа заявок, обеспечивающих максимальную производительность вычислительной системы, если средняя длина очереди не должна превышать k.

Обратим внимание. Целевая функция F(x) – не обязательно функция, заданная в аналитической форме, в виде какого-либо аналитического выражения. В общем виде критерий оптимальности представляет собой некоторый механизм, позволяющий по значениям входных параметров определить значения наиболее существенных характеристик объекта. (некоторое отображение между множествами входных и выходных параметров)

При этом математическая модель объекта проектирования может быть:

1) функциональной, представляющей собой систему уравнений, которая отображает физические или информационные процессы в объекте;

2) аналитической, представляет собой совокупность аналитических зависимостей между входными и выходными параметрами;

3) алгоритмической, представляет собой алгоритм вычисления выходных параметров по значениям входных параметров (“черный ящик”);

- имитационной, частном случае алгоритмической модели, отражает поведение объекта при заданных изменяющих во времени параметрах.

Обобщенная схема принятия оптимальных решений.

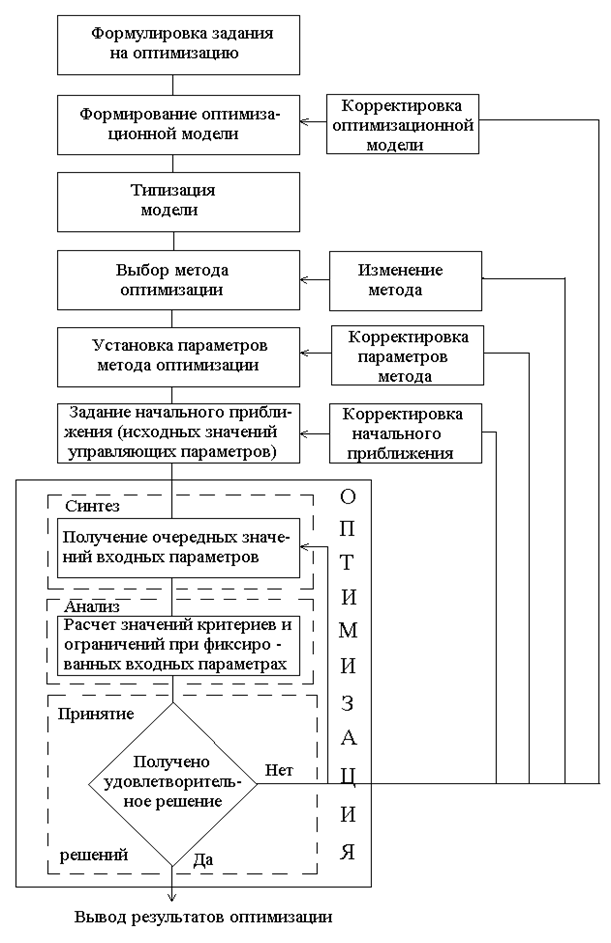
На этапе формирования задания на оптимизацию осуществляется содержательная постановка задачи, т.е. определяются наиболее важные варьируемые параметры, требования к ним, определяются критерии оптимальности. На этом этапе дается словесная, начальная постановка задачи. Обычно этот этап выходит за пределы математики.

Построение оптимизационной модели связано с формализацией содержательной постановки задачи, т.е. с записью ее с использованием математических соотношений в форме (1). При этом необходимо определить взаимосвязи между входными и выходными параметрами и задать критерии оптимальности и функциональные ограничения в аналитической или алгоритмической форме. Этот этап связан также с нормированием (или нормализацией) управляющих параметров. Различают линейную нормализацию

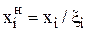, где x_i – константа, равная единице измерения параметра x_i и логарифмическую нормализацию

.

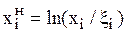Преимущество логарифмической нормализации – оперирование относительными приращениями параметров.

Типизация модели связана с ее преобразованием и приведением к виду, пригодному для использования стандартных оптимизационных процедур.

Выбор метода оптимизации – очень важная задача, оказывающая большое влияние на результат оптимизации. Задачи оптимизации и методы делятся классы, для каждого из которых разработаны свои алгоритмы решения. Но даже в рамках одного класса для решения оптимизационных задач могут быть использованы различные оптимизационные процедуры. Не существует универсального алгоритма, эффективно решающего все оптимизационные задачи. Один и тот же алгоритм при решении различных задач может показывать различную эффективность. Поэтому на практике часто используется многометодный режим решения задач оптимизации.

Далее устанавливаются параметры (постоянные величины) в зависимости от выбранного метода.

Выбор начального приближения, также играет важную роль. От качества начального приближения зависит результат оптимизации.

Сам процесс оптимизации представляет собой итерационную последовательность процедур синтеза, анализа и принятия решений. На этапе синтеза в соответствии с выбранным алгоритмом определяются очередные значения входных параметров (т.е., синтезируется очередной вариант сочетания значений параметров). Этап анализа связан с оценкой полученного варианта, т.е. с вычислением значений показателей качества и ограничений, соответствующих полученным значениям входных параметров. На этапе принятия решений определяется, является ли данный вариант удовлетворительным. Если получаем приемлемый вариант, процесс оптимизации заканчивается, если нет – продолжается, т.е. осуществляется переход на следующую итерацию. Обычно в вычислительных процедурах оптимизации проверка качества получаемого варианта осуществляется автоматически. При этом на начальном этапе оптимизации определяется критерий останова алгоритма, при выполнении которого он заканчивает работу. На каждой итерации осуществляется автоматическая проверка критерия останова и в случае его невыполнения итерационный процесс оптимизации продолжается.

Если критерий останова выполнен (алгоритм оптимизации закончил работу), но проектировщика данный вариант объекта не устраивает, можно осуществить следующие действия:

1) скорректировать начальное приближение;

2) изменить параметры метода;

3) изменить метод;

4) скорректировать оптимизационную модель.

Прикладные линейные модели

Рассмотрим основные приемы построения математических моделей для некоторых типовых задач линейного программирования.

1. Задача определения производственного плана.

Для изготовления n видов продукции A₁,…,A_n необходимы ресурсы S₁,…,S_m (сырье, рабочая сила, оборудование и т.д.). Заданы значения a_ij, которые характеризуют количество ресурса S_i , необходимого для выпуска единицы продукции A_j. Запас каждого ресурса S_i ограничен и равен b_i . От реализации единицы продукции A_j может быть получена прибыль c_j. Необходимо так составить производственный план (т.е. определить, сколько продукции каждого вида необходимо выпустить), чтобы общая прибыль от производства всей продукции была максимальной.

Исходные данные задачи можно удобно представить в виде табл.1:

Таблица 1

Ресурсы	Виды продукции	Запасы ресурсов
A1	A2	…	An
S1 S2 … Sm	a11 a21 ... am1	A12 a22 ... am2	... ... ... ...	A1n a2 n ... amn	b1 b2 ... bm
Прибыль	c1	c2	…	cn

Обозначим через x_j количество продукции A_j, которое необходимо выпустить по плану. Тогда математическая модель данной задачи имеет следующий вид:

c₁x₁+ c₂x₂+...+ c_nx_n ®max;

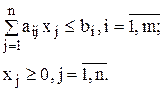
Здесь целевая функция – это общая прибыль от производства всей продукции. Каждое i-е ограничение характеризует общее количество ресурса S_i для производства всей продукции, которое не должно превышать величины b_i. Кроме ограничения по ресурсам, в условия задачи (а, следовательно, и в ее математическую модель) могут вводиться дополнительные ограничения на планируемый выпуск продукции (ограничения по ассортименту, условия комплектности и т.д.).

Пример. Требуется определить, в каком количестве необходимо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4 для изготовления которой требуются ресурсы трех видов: трудовые ресурсы, сырье, финансы. Нормы расхода ресурсов каждого вида для выпуска единицы продукции, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в табл. 2. Количество расходуемых ресурсов не должно превышать имеющихся запасов.

Таблица 2

Ресурсы	Виды продукции	Запасы ресурсов
Прод. 1	Прод. 2	Прод.3	Прод.4
Трудовые
Сырье
Финансы
Прибыль

Математическая модель для решения данной задачи будет иметь следующий вид:

F=7x₁+3x₂+6x₃+12x₄®max;

3x₁+x₂+2x₃+4x₄ £440;

x₁+8x₂+6x₃+2x₄ £200;

x₁+4x₂+7x₃+2x₄ £320;

x_j ³0, j= .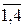

2. Задача о смесях.

Имеется набор компонентов A₁,…,A_n, при сочетании которых в разных пропорциях образуются различные смеси. В состав каждого компонента входят вещества P₁,…,P_m. Через a_ij обозначим количество вещества P_i в единице компонента A_j. В смеси необходимо обеспечить содержание вещества P_i (обозначим его через b_i ). Цена единицы компонента A_j равна c_j. Необходимо определить состав смеси (т.е., количество компонентов каждого вида), цена которой окажется минимальной. Исходные данные задачи представлены в табл.3:

Таблица 3

Вещества	Компоненты смеси	Минимально необходимое количество веществ
A1	A2	…	An
P1 P2 … Pm	a11 a21 ... am1	A12 a22 ... am2	... ... ... ...	A1n a2 n ... amn	b1 b2 ... bm
Цена	c1	c2	…	cn

Обозначим через x_j количество компонента A_j, которое необходимо включить в смесь. Тогда математическая модель данной задачи имеет следующий вид:

c₁x₁+ c₂x₂+...+ c_nx_n ®min;

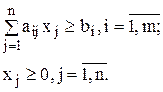
Здесь целевая функция характеризует цену смеси, которая должна быть минимальной. Каждое i-е ограничение характеризует общее количество вещества P_i в смеси. Кроме ограничений по содержанию отдельных веществ в смеси, в задаче могут быть использованы ограничения по имеющимся запасам отдельных компонентов или по предельным нормам их включения в смесь. Могут задаваться также пропорции, в которых некоторые из компонентов должны входить в состав смеси.

Пример Фирма занимается составлением диеты, состоящей из трех продуктов (мясо, крупы, молоко) и содержащей не более 26 единиц углеводов, не менее 16 единиц витаминов и не более 60 единиц белков. Как дешевле всего достичь этого при указанных в табл. 4 количествах углеводов, витаминов и белков в единице каждого продукта?

Таблица 4

Вещества	Виды продуктов	Предельное количество веществ в диете
Мясо	Крупы	Молоко
Углеводы
Витамины
Белки
Цена

Математическая модель данной задачи имеет вид:

F=6x₁+x₂+x₃®min;

2x₁+4x₂+5x₃ £26;

4x₁+2x₂³16;

12x₁+3x₂+x₃ £60;

x_j ³0, j= .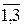

3. Задача о комплектах.

Пусть планируется производство комплектных изделий. Каждое изделие содержит m видов деталей, причем деталей первого вида - k₁ единиц, деталей второго вида k₂ единиц, деталей j-го вида k_j единиц. Изделия могут изготавливаться n различными исполнителями. Пусть в единицу времени i-й исполнитель может изготовить a_ij элементов j-го вида. Сдаче подлежат только комплектные изделия. Каждый i-й исполнитель работает не более b_i часов. Определить такой план загрузки исполнителей, чтобы общее число выпускаемых комплектных изделий было максимальным.

Обозначим через 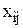- время изготовления деталей j-го вида i-м исполнителем. Тогда общее число деталей j-го вида, изготавливаемых всеми исполнителями, определится в виде

, .

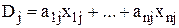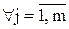Общее количество изделий, для выпуска которых хватит деталей j-го типа при условии, что k_j единиц расходуется на одно изделие равно

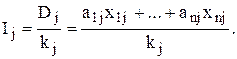
Тогда общее число комплектов определится следующим образом:

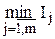
В результате математическую модель задачи можно сформулировать в виде:

=

, ;

.

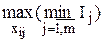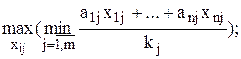
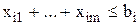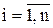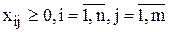Для формализации данной постановки в виде задачи линейного программирования введем новую переменную:

,

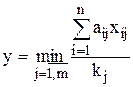что равносильно записи

.

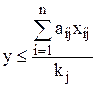
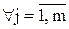Тогда окончательный вид математической модели задачи:

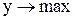
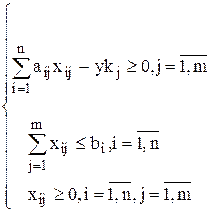
Симплекс-метод

Основным методом решения ЗЛП является симплексный метод. Перед его использованием ЗЛП необходимо привести к канонической форме записи. При этом используются следующие приемы:

1. Для перехода от задачи максимизации к задаче минимизации целевую функцию необходимо умножить на –1.

2. Переменные, на которых не наложено ограничение неотрицатель-ности, заменяются во всех ограничениях и в целевой функции разностью двух неотрицательных переменных

x_j = u_j- w_j u_j, w_j ³ 0.

3. Переход к ограничениям с неотрицательными правыми частями осуществляется умножением левой и правой частей ограничений с отрицательными правыми частями на –1. При этом знаки соответствующих неравенств меняются на противоположные.

4. Переход от ограничений-неравенств к ограничениям-равенствам производится путем введения дополнительных неотрицательных переменных. При этом если знак неравенства £, дополнительная переменная прибавляется к левой части ограничения, а если ³, то вычитается. Таким образом, ограничение-неравенство

a_i1x₁ + a_i2x₂ +…+ a_inx_n £ b_i

преобразуется в ограничение-равенство

a_i1x₁ + a_i2x₂ +…+ a_inx_n + x_n+1 = b_i (x_n+1 ³ 0),

где x_n+1 – дополнительная переменная, x_n+1³0.

Ограничение-неравенство:

a_i1x₁ + a_i2x₂ +…+ a_inx_n ³ b_i

преобразуется в ограничение-равенство следующим образом:

a_i1x₁ + a_i2x₂ +…+ a_inx_n - x_n+1 = b_i (x_n+1 ³ 0)

В каждое ограничение-неравенство вводится своя дополнительная переменная. Число вводимых дополнительных неотрицательных переменных равно числу преобразуемых неравенств.

Рассмотрим ЗЛП в канонической форме:

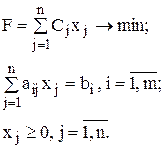
Вектор X = (x_1,…, x_n), удовлетворяющий системе ограничений ЗЛП, называется допустимым решением или планом.

План, X^*=(x₁^*,…,x_n^*), при котором целевая функция принимает оптимальное значение, называется оптимальным.

Перепишем ЗЛП в векторной форме.

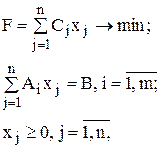
где A₁,…,A_n – m-мерные вектор-столбцы, составленные из коэффициентов при переменных в системе ограничений:

.

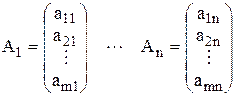B – вектор-столбец свободных членов системы ограничений:

.

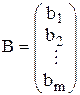План X = (x_1,…, x_n) называется опорным планом ЗЛП, если система векторов А_j, входящих в разложение 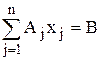с положительными коэффи-циентами x_j , линейно независима. Так как векторы А_j являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше, чем m.

Симплексный метод решения ЗЛП основан на переходе от одного опорного плана к другому, при котором значение целевой функции убывает. Указанный переход возможен, если известен какой-нибудь исходный опорный план. Такой план можно легко указать, если ЗЛП записана в форме:

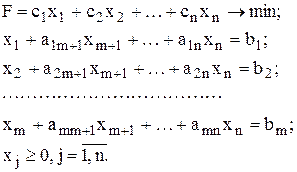
Векторная форма данной задачи имеет вид:

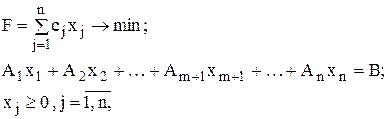
где

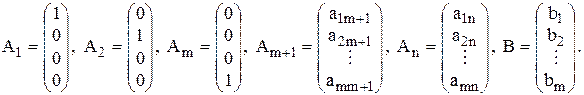
Переменные, которые входят только в одно уравнение системы ограничений с коэффициентом равным 1, называют базисными переменными (в рассматриваемом примере это переменные x₁… x_m). Остальные переменные называются свободными. Тогда, приравнивая базисные переменные соответствующим правым частям ограничений, а свободные переменные нулю, получим опорный план X = (b₁, b₂,…, b_m,0 ,…,0), определяемый системой единичных векторов, А₁,…, А_m , которые образуют базис m-мерного пространства.

Для удобства расчетов в симплексном методе все данные по задаче аносят в симплекс-таблицу:

Таблица 5

xd	сd	B	с1	c2	…	cn
X1	x2	…	xn
xd1	cd1	b1	A11	a12	…	a1n
xd2	cd2	b2	A21	a22	…	a2n
…	…	…	…	…	…	…
xdm	cdm	bm	Am1	am2	…	amn
F		D1	D2	…	Dn

В верхнюю строку таблицы заносятся коэффициенты при всех переменных в целевой функции. В первом столбце таблицы записываются базисные переменные в той последовательности, в которой они входят в систему ограничений, во втором – коэффициенты целевой функции при базисных переменных, в третьем – правые части всех ограничений, в последующих столбцах – коэффициенты при соответствующих переменных в системе ограничений. В нижней строке таблицы записываются оценки по каждой переменной, определяемые следующим образом: 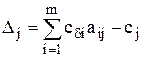. Очевидно, что для базисных переменных оценки равны нулю.

На каждой итерации симплекс-метода осуществляется вывод из базиса какой-либо переменной и включение в него другой переменной с соответствующим пересчетом элементов таблицы. Перед решением задачи ее необходимо привести к канонической форме.

Основные шаги симплекс – метода:

1. Определение начального опорного плана.

2. Составление симплекс-таблицы.

3. Вычисление оценок .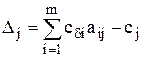

4. Анализ оценок.

4.1. Если 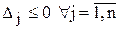, то получено оптимальное решение.

4.2. Если существует хотя бы одна оценка D_j > 0 , для которой 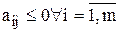, то целевая функция не ограничена снизу на множестве допустимых решений (ЗЛП не имеет решения).

4.3. Из всех оценок D_j > 0 выбирается максимальная: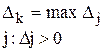

Переменная x_k, которой соответствует максимальная оценка, стано-

вится на текущей итерации базисной, а k-й столбец объявляется

ведущим столбцом.

5. Определение ведущей строки. Для этого находятся отношение правых частей ограничений к положительным элементам ведущего столбца и среди них выбирается минимальное:

.

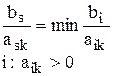S-я строка объявляется ведущей строкой. Элемент, находящийся в симп-

лекс-таблице на пересечении s-й строки и k-го столбца a_sk, называется ведущим элементом.

6. Пересчет элементов симплекс-таблицы.При этом элементы ведущей строки a_s1,…, a_sn, b_s делятся на ведущий элемент a_sk. Пересчет остальных элементов осуществляется по правилу прямоугольника.

	k-й столбец		j-й столбец
s-я строка	ask		аsj
i-я строка	aik		аij

Пусть a_sk – ведущий элемент. Элемент a_ij– пересчитывается следующим образом:

.

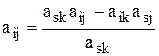7. Переход к шагу 3

Оптимальное решение определяется следующим образом: базисные переменные приравниваются соответствующим правым частям, остальные нулю.

Пример

x₁-x₂-3x₃®min

2x₁-x₂+x₃ £ 1

4x₁-2x₂+x₃ ³ -2

3x₁+x₃ £ 5

x₁, x₂, x₃ ³ 0

Приведем к каноническому виду

x₁-x₂-3x₃®min

2x₁-x₂+x₃+x₄ = 1

-4x₁+2x₂-x₃+x₅ = 2

3x₁+ x₃+x₆ = 5

x₁, x₂, x₃ ³ 0

Составим “симплекс-таблицу”:

xб	Сб	b		-1	-3
x1	x2	x3	x4	x5	x6
x4				-1
x5			-4		-1
x6
	-1
x3	-3			-1
x5			-2
x6						-1
-3	-7			-3
x3	-3
x2	-1		-2
x6						-2	-1
-15				-7	-4
x3	-3
x2	-1	11/3				-1/3	1/3	2/3
x1		1/3				-2/3	-1/3	1/3
-46/3				-19/3	-11/3	-1/3

Оптимальное решение:

x₁=1/3; x₂=11/3; x₃=4; x₄=0; x₅=0; x₆=0.

Метод искусственного базиса

Как было указано выше, решение ЗЛП симплексным методом начинается с указания какого-либо первоначального опорного плана. Для ЗЛП, записанной в канонической форме, можно непосредственно указать опорный план, если среди векторов A_j, компонентами которых служат коэффициенты при переменных в системе ограничений данной задачи, есть m единичных (т.е., имеются m базисных переменных). Однако для многих ЗЛП, записанных в канонической форме, не всегда можно сразу определить опорный план. Рассмотрим задачу

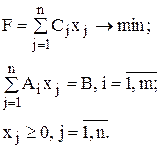
Пусть в данной задаче среди векторов

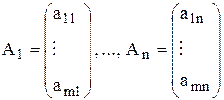нет единичных.

В данном случае к каждому i-му уравнению системы ограничений добавляется неотрицательная переменная x_n+i , называемая искусственной переменной. Так как введение искусственных переменных, в отличие от дополнительных, меняет множество решений задачи, то они вводятся также и в выражение для целевой функции с очень большим коэффициентом M > 0 (тогда в процессе решения задачи минимизации искусственные переменные будут стремиться к нулю). В результате получается задача, называемая расширенной по отношению к исходной:

;

;

.

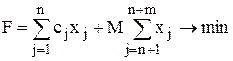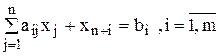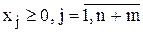В результате может быть указан первоначальный опорный план. Искусственные переменные приравниваются к правым частям (x_n+i=b_i), остальные – нулю ( 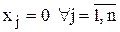). Тогда целевая функция примет вид:

,

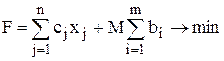а оценки D_j в данном случае будут складываться из двух частей, одна из которых зависит от М, а другая не зависит:

.

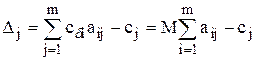Исходные данные расширенной задачи заносят в симплекс-таблицу, которая содержит на строку больше, чем обычная. В последнюю, (m + 2)-ю строку оценок таблицы записывают коэффициенты при M, а в (m + 1)-ю - слагаемые, не содержащие M.

Так как знак D_j определяется знаком коэффициента, стоящего при M, ведущий столбец (и соответственно базисную переменную) выбирают по наибольшему положительному элементу (m + 2)-й строки таблицы. Пересчет симплекс-таблицы при переходе от одного опорного плана к другому производят по общим правилам симплексного метода. Итерационный процесс по (m + 2)-й строке ведут до тех пор, пока

1) либо все искусственные переменные не будут исключены из базиса;

2) либо не все искусственные переменные будут исключены, но (m + 2)-я

строка не содержит больше положительных элементов.

В первом случае полученное базисное решение соответствует некоторому опорному плану исходной задачи, (m+2)-я строка таблицы вычеркивается и решение задачи продолжают обычным симплексными методом. Во втором случае, если элемент, стоящий в (m + 2)-й строке столбца B положителен, задача не имеет решения, если он равен нулю, то базис содержит по крайней мере один из векторов искусственного базиса.

Если в процессе решения задачи какая-либо искусственная переменная выводится из базиса, то соответствующий столбец симплекс-таблицы можно вычеркнуть и не пересчитывать (т.к. эту переменную не имеет смысла вводить ни в один из последующих базисов).

Рассмотренный метод построения начального опорного плана называется методом искусственного базиса.

Таким образом алгоритм метода включает следующие шаги:

1. Составляется расширенная задача

2. Находится опорный план решения задачи

3. С использованием симплекс-метода искусственные переменные исключаются из базиса. В результате получается некоторый опорный план исходной задачи.

4). Нахождение оптимального плана исходной задачи с использованием симплекс-метода.

Пример:

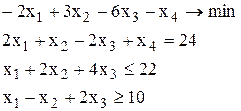
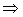
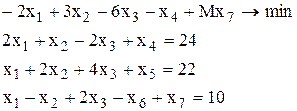
xб	Сб	b	-2		-6	-1			M
x1	x2	x3	x4	x5	x6	x7
x4	-1				-2
x5
x7	M			-1				-1
-24		-4
		-1				-1
x4	-1							-1
x5			-1
x3	-6		1/2	-1/2				-1/2
-64	-4
x4	-1		5/2				1/2
x6			-1/2				1/2
x3	-6	11/2	1/4	1/2			1/4
-68	-2	-8			-2

Ответ: x^*=(0; 0; 11/2; 35; 0; 1).

Двойственность в линейном программировании

Каждой ЗЛП можно поставить в соответствие двойственную в соответствии с следующими правилами:

1) если целевая функция F исходной задачи стремится к минимуму, то целевая функция Ф двойственной задачи – к максимуму и наоборот;

2) число переменных двойственной задачи равно числу ограничений исходной, число ограничений двойственной задачи равно числу переменных исходной. Каждому i-му ограничению исходной задачи соответствует переменная y_i двойственной задачи (двойственная переменная), а каждой j-й переменной исходной задачи соответствует j-е ограничение исходной задачи;

3) коэффициентами при переменных целевой функции двойственной задачи являются правые части ограничений исходной задачи, а правыми частями ограничений двойственной задачи являются коэффициенты при целевой функции в исходной задаче;

4) матрица коэффициентов при двойственных переменных в системе ограничений двойственной задачи является транспонированной матрицей коэффициентов при переменных в ограничениях исходной задачи;

5) для удобства построения двойственных задач рекомендуется в исходной задаче ограничения-неравенства записывать со знаком “£ ” при максимизации и со знаком “ ³” при минимизации;

6) каждому i-му ограничению – неравенству исходной задачи соответствует в двойственной задаче условие неотрицательности (y_i³0), а ограничению -равенству - переменная y_i произвольного знака;

7) неотрицательной переменной исходной задачи x_j³0 соответствует в двойственной задаче j-е ограничение – неравенство, а произвольной переменной x_j - равенство. При этом если двойственная задача подлежит минимизации, неравенство записывается со знаком “ ³”, а если двойственная задача подлежит макси