Двойственной задаче об использовании ресурсов
В гл. 2 рассмотрена задача об использовании ресурсов. (экономико-математическая модель и содержательная интерпретация этой задачи I представлены в левой части табл. 5.1). В приведенной модели 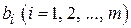 обозначает запас ресурса
обозначает запас ресурса 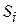 ;
; 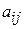 − число единиц ресурса
− число единиц ресурса 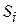 потребляемого при производстве единицы продукции
потребляемого при производстве единицы продукции 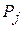
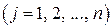 ;
; 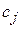 − прибыль (выручка) от реализации единицы продукции
− прибыль (выручка) от реализации единицы продукции 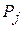 (или цена продукции
(или цена продукции 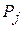 ).
).
Предположим, что некоторая организация решила закупить ресурсы 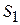 ,
, 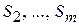 предприятия и необходимо установить оптимальные цены на эти ресурсы
предприятия и необходимо установить оптимальные цены на эти ресурсы 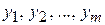 .
.
Очевидно, что покупающая организация заинтересована в том, чтобы затраты на все ресурсы 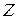 в количествах
в количествах 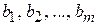 по ценам соответственно
по ценам соответственно 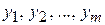 были минимальны, т.е
были минимальны, т.е
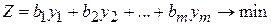 .
.
С другой стороны, предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не менее той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию. На изготовление единицы продукции 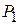 расходуется
расходуется 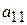 единиц ресурса
единиц ресурса 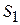 ,
, 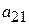 единиц ресурса
единиц ресурса 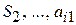 единиц ресурса
единиц ресурса 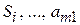 единиц ресурса
единиц ресурса 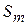 по цене соответственно
по цене соответственно 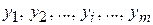 . Поэтому для удовлетворения требований продавца затраты на ресурсы, потребляемые при изготовлении единицы продукции
. Поэтому для удовлетворения требований продавца затраты на ресурсы, потребляемые при изготовлении единицы продукции 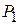 , должны быть не менее ее цены
, должны быть не менее ее цены 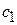 , т.е.
, т.е.
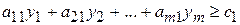 .
.
Аналогично можно составить ограничения в виде неравенств по каждому виду продукции 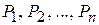 . Экономико-математическая модель и содержательная интерпретация полученной таким образом двойственной задачи II приведены в правой части табл. 1.
. Экономико-математическая модель и содержательная интерпретация полученной таким образом двойственной задачи II приведены в правой части табл. 1.
Таблица 1.
| Задача I (исходная) | Задача II (двойственная) |
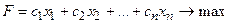 при ограничениях: при ограничениях: 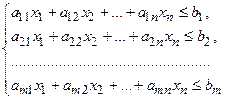 и условии неотрицательности и условии неотрицательности 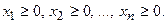 Составить такой план выпуска продукции Составить такой план выпуска продукции  , при котором прибыль (выручка) от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов , при котором прибыль (выручка) от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов | 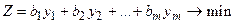 ) при ограничениях: ) при ограничениях: 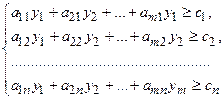 и условии неотрицательности и условии неотрицательности 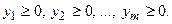 Найти такой набор цен (оценок) ресурсов Найти такой набор цен (оценок) ресурсов 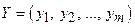 , при котором общие затраты на ресурсы будут минимальными при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли (выручки) от реализации этой продукции , при котором общие затраты на ресурсы будут минимальными при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли (выручки) от реализации этой продукции |
Цены ресурсов 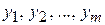 в экономической литературе получили различные названия: учетные, неявные, теневые. Смысл этих названий состоит в том, что это условные, "ненастоящие" цены. В отличие от "внешних" цен
в экономической литературе получили различные названия: учетные, неявные, теневые. Смысл этих названий состоит в том, что это условные, "ненастоящие" цены. В отличие от "внешних" цен 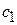 ,
, 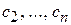 на продукцию, известных, как правило, до начала производства, цены ресурсов
на продукцию, известных, как правило, до начала производства, цены ресурсов 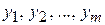 являются внутренними, ибо они задаются не извне, а определяются непосредственно в результате решения задачи, поэтому их чаше называют оценками ресурсов.
являются внутренними, ибо они задаются не извне, а определяются непосредственно в результате решения задачи, поэтому их чаше называют оценками ресурсов.
Пример выполнения задания
Задача
Пусть задана математическая модель в стандартном виде задачи линейного программирования:
12x1 + Зx2 ≤ 264;
4x1 + 5x2 ≤ 136; (1)
Зx1 + 14x2 ≤ 266;
x1 ≥ 0; x2 ≥ 0.
Z = 6x1 + 4x2 → МАХ.
Решение
Составим по модели (1) математическую модель двойственной задачи. Для этого выпишем расширенную матрицу задачи (1):
x1 x2 св.ч.
А= 
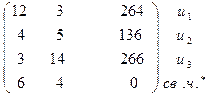
 (2)
(2)
Математические модели взаимно-двойственных задач связаны между собой по правилам:
1) одна из задач содержит столько неравенств-ограничений (или равенств), сколько неизвестных у другой;
2) расширенные матрицы обеих задач транспонированы по отношению друг к другу;
3) одна задача имеет ограничения 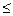 и целевую функцию на максимум, а другая – ограничения
и целевую функцию на максимум, а другая – ограничения 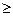 и целевую функцию на минимум;
и целевую функцию на минимум;
4) свободные члены системы ограничений и коэффициенты целевой функции меняются местами;
5) каждому ограничению-неравенству соответствует неотрицательная двойственная переменная, а равенству – переменная без ограничения знака ( и наоборот).
Из (2) получаем двойственную задачу в виде:
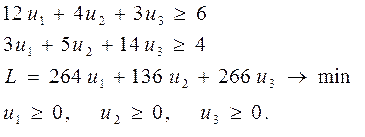 (3)
(3)
Двойственная задача линейного программирования имеет простой экономический смысл. В исходной задаче неравенства описывали ограничения по ресурсам и требовалось найти план, обеспечивающий максимум прибыли при заданных нормах расхода каждого ресурса на изделие.
В двойственной задаче переменные 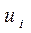 имеют смысл оптимальных цен единицы каждого ресурса. Ограничения означают, что стоимость сырья, израсходованного на единицу изделия j (j=1,2), должна обеспечивать его продавцу прибыль не менее, чем прибыль от продажи единицы этого изделия. Цель заключается в том, чтобы общая стоимость ресурсов была минимальной с точки зрения покупателя.
имеют смысл оптимальных цен единицы каждого ресурса. Ограничения означают, что стоимость сырья, израсходованного на единицу изделия j (j=1,2), должна обеспечивать его продавцу прибыль не менее, чем прибыль от продажи единицы этого изделия. Цель заключается в том, чтобы общая стоимость ресурсов была минимальной с точки зрения покупателя.
Таким образом, двойственная задача заключается в определении оптимальных оценок (условных цен) единицы каждого ресурса при условии минимальной суммарной стоимости ресурсов.
Справедливы две теоремы двойственности.
Первая (основная) теорема. Если одна из двойственных задач имеет оптимальное решение, то и другая его имеет, причем значения их целевых функций для оптимальных решений совпадают. Если одна из двойственных задач не имеет оптимального решения, то двойственная ей задача противоречива.
Из основной теоремы двойственности вытекает, что существование оптимальных решений двойственных ЗЛП гарантируется наличием хотя бы одного допустимого плана для каждой из двойственных задач, причем оптимальные значения целевых функций совпадут.
Отсюда следует, что решение обеих двойственных задач симплекс-методом можно совместить в одних симплекс-таблицах. Кроме того, зная решение одной из двойственных задач, можно найти решение другой задачи, пользуясь второй теоремой двойственности.
Вторая теорема двойственности. Для оптимальных решений пары симметричных двойственных задач выполняются две группы сопряженных условий:
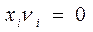 , (4)
, (4)
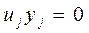 , (5)
, (5)
где 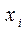 и
и 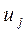 – основные и двойственные переменные, а
– основные и двойственные переменные, а 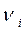 и
и 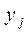 – дополнительные выравнивающие переменные (искусственный базис двойственной и исходной задач соответственно).
– дополнительные выравнивающие переменные (искусственный базис двойственной и исходной задач соответственно).
В нашем примере
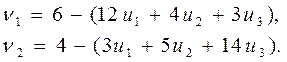 (6)
(6)
Получаем из (4) и (5) систему
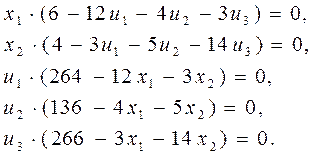 (7)
(7)
Подставим в (7) найденные выше х1=19, х2=12, для двойственных переменных получим систему линейных алгебраических уравнений
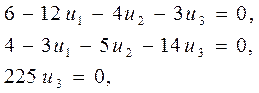 (8)
(8)
решая которую, находим решение двойственной задачи:
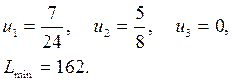
Задача 2.
Рассмотрим модель ценообразования, которая базируется на балансе спроса и предложения.
Пусть имеем m технологических процессов. Каждый из них описывается вектором 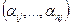 , где
, где 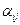 – выпуск i-го продукта на каждую единицу интенсивности j-го технологического процесса. Пусть j-й процесс требует на каждую единицу интенсивности процесса
– выпуск i-го продукта на каждую единицу интенсивности j-го технологического процесса. Пусть j-й процесс требует на каждую единицу интенсивности процесса 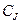 единиц труда. Задача состоит в том, чтобы найти интенсивности z1, z2,…,zm:
единиц труда. Задача состоит в том, чтобы найти интенсивности z1, z2,…,zm:
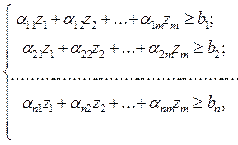 (9)
(9)
где bi – необходимый выпуск i-го продукта, i =1,…,n. При этом общие затраты труда должны быть минимальными:
с1z1+c1z2+…+cmzm→min. (10)
Определение оптимальных цен продуктов основывается на решении задачи, которая является двойственной к задаче (9) – (10).
Пусть Цi – цена единицы i-го продукта, тогда двойственная задача имеет вид:
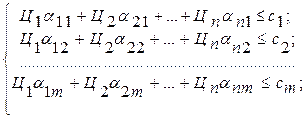 (11)
(11)
b1Ц1+b2Ц2+…+bnЦn→max. (12)
Экономическая интерпретация двойственной задачи: стоимость выпуска продукции в каждом технологическом процессе не должна превышать затраты труда (условия (11)). Общий выпуск продукции максимизируется (условие (12)).
Рассмотрим пример ценообразования по двойственной задаче.
Пусть n =2, m =3 и матрица 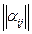 имеет вид:
имеет вид:
Таблица 2.
| Технологические процессы | z1 | z2 | z3 | Необходимый выпуск bi |
| Продукт 1 | ||||
| Продукт 2 | ||||
| Затраты труда сj |
Прямая задача:минимизация затрат труда
К =31Z1+11Z2+12Z3→min
при ограничениях:
z1+z2+2z3≥21; 2z1+z2+z3≥12.
Решение задачи: z1 =0; z2 =3; z3 =9, К =141.
Двойственная задача:максимизация выпуска
W =21Ц1+12Ц2→max
при ограничениях:
Ц1+2Ц2≤31; Ц1+Ц2≤11; 2Ц1+Ц2≤12.
Решение задачи:z1 =0; z2 =3; z3 =9; W =141.
Таким образом, К =W, что соответствует теории двойственности.
Задание к практическому занятию:
Базовый уровень:
Задание 1. Для условий таблицы 5.3. сформулировать двойственную задачу и решить ее.
Таблица 3. Варианты заданий
| Вариант | Задача | Вариант | Задача |
Z(X)=x1+4x2+x3®max, 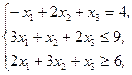 xj³0, j=1,2,3 xj³0, j=1,2,3 | Z(X)=-2x1-2x2-2x3®min, 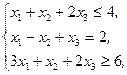 xj³0, j=1,2,3 xj³0, j=1,2,3 | ||
Z(X)=2x1+x2-x3®min, 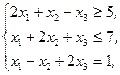 xj³0, j=1,2,3 xj³0, j=1,2,3 | Z(X)=-3x1-2x2-2x3®min, 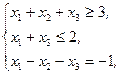 xj³0, j=1,2,3 xj³0, j=1,2,3 | ||
Z(X)=x1-x2+x3®max, 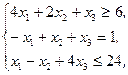 xj³0, j=1,2,3 xj³0, j=1,2,3 | Z(X)=-2x1+8x2+3x3®min, 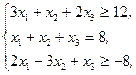 xj³0, j=1,2,3 xj³0, j=1,2,3 | ||
Z(X)=5x1+2x2+x3®max, 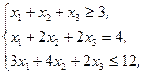 xj³0, j=1,2,3 xj³0, j=1,2,3 | Z(X)=6x1+7x2+9x3®min, 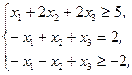 xj³0, j=1,2,3 xj³0, j=1,2,3 | ||
Z(X)=x1-8x2-3x3®max, 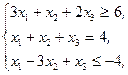 xj³0, j=1,2,3 xj³0, j=1,2,3 | Z(X)=5x1+2x2+x3®max, 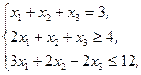 xj³0, j=1,2,3 xj³0, j=1,2,3 |
Повышенный уровень:
Задание 2.
В заданиях 2.1.- 2.4. методом Гомори (или методом ветвей и границ) найти оптимальные решения задач целочисленного линейного программирования. Дать геометрическую интерпретацию процесса решений задач.
Задание 2.1. 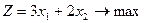 Задание 2.2.
Задание 2.2. 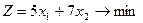
при ограничениях: при ограничениях:
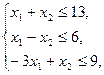
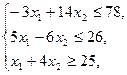
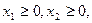
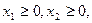
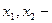 целые числа.
целые числа. 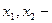 целые числа.
целые числа.
Задание 2. 3. 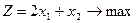 Задание 2. 4.
Задание 2. 4. 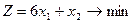
при ограничениях: при ограничениях:
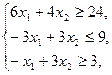
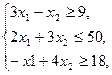
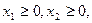
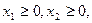
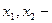 целые числа.
целые числа. 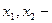 целые числа.
целые числа.
Вопросы для самостоятельной работы
Базовый уровень:
- Дайте характеристику двойственных ЗЛП.
- Сформулируйте алгоритм составления двойственной задачи.
- Сформулируйте основные теоремы теории двойственности.
- Каков экономический смысл теории двойственности?
- Что называют объективно обусловленными оценками?
- Чем отличаются задачи целочисленного программирования, от других ЗЛП?
Повышенный уровень:
- В чем суть метода ветвей и границ?
8. В чем состоит метод Гомори?
9. Сколько оптимальных решений может иметь задача целочисленного программирования?
