Решение задачи методом потенциалов
1. Введем вспомогательные величины, называемые потенциалами:
- 
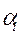– потенциалы поставщиков (строк),
-βj– потенциалы потребителей (столбцов).
Проставим буквенные обозначения для потенциалов: для поставщиков
2. Потенциалы вычисляются из условия:
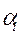+ βj = Cij – для заполненных клеток, где Сij – тарифы этих клеток. В нашей задаче:
|
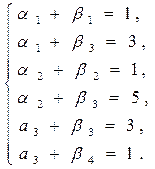
3. Значение одного из потенциалов выбираем произвольно. Например,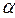 
1 = 0. Тогда значения остальных потенциалов легко найдутся из указанной системы:
β1=1; β3 = 3;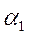 
= 2; 
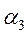= 0; β3 = -1; β4 = 1.
Эти значения потенциалов проставим в таблице 4.6 сверху и слева.
4. Проверим план на оптимальность. Оптимальный план должен удовлетворять условию:
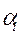+ βj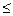 
Cij – для пустых клеток.
Проверяем все пустые клетки:
клетка (1;2) 0 + (-1) < 2;
|
клетка (2;1) 2 + 1 > 2;
клетка (2;4) 2 + 1 = 3;
клетка (3;1) 0 + 1 < 8;
клетка (3;2) 0 + (-1) < 6;
Как показывают вычисления, для клетки (2;1) условие оптимальности не выполняется, следовательно план не оптимален и его нужно улучшать. Для этого загружаем «неоптимальную» клетку (2;1) (или одну из них, если их несколько) за счет перераспределения груза в других клетках.
Для того чтобы осуществить перераспределение груза, построим цикл пересчета к «неоптимальной» клетке.
Циклом называется многоугольник, у которого:
1) все стороны лежат в строках и столбцах;
2) все углы прямые;
3) все вершины лежат в заполненных клетках, а одна вершина – в свободной неоптимальной клетке;
4) в цикл включены лишь те клетки, где находятся его вершины.
Циклы пересчета могут иметь следующую форму (рис. 2):
1) 2) 3)
| |
Рисунок 2
Число их вершин обязательно четно. «Неоптимальная» клетка может находиться в любой вершине цикла. Для определенности «неоптимальная» клетка каждого цикла отмечается вопросом или знаком «+».
По циклу будем перемещать поставку. Для нахождения величины этой поставки сначала проставим знаки в вершинах цикла: в «неоптимальную» клетку ставим знак «+»(плюс), а далее, совершая обход по циклу, чередуем знаки «-» (минус) и «+»(плюс) в его вершинах. Из клеток, отмеченных знаком «-» (минус), выбираем наименьшую поставку.
В нашей задаче цикл, составленный к клетке (2;1),. В него входят клетки (2;1), (1;1). (1;3). (2;3). Наименьшая из поставок, отмеченных знаком «-», равна 10: min {100;10} = 10. Перемещаем ее по циклу. При этом прибавляем по 10 единиц к поставкам, находящимся в вершинах со знаком «+», вычитаем по 10 единиц из поставок, находящихся в вершинах со знаком «-». В результате всех этих перемещений приходим к новому плану
Таблица 4.
| Базы | Потребители | Запасы | |||
| β1 = 1 В1 | β2 = 0 В2 | β3 = 3 В3 | β4 = 1 В4 | ||
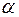 1 =0; А1 | 90 1 | 2 | 30 3 | 4 | |
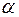| 2=1; А2 | 10 2 | 70 1 | 5 | 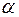3 | |
| 3=0; А3 | 8 | 6 | 20 3 | 20 1 | |
| Потребности |
Этот план является опорным, т. к. удовлетворяет всем признакам опорного плана:
1) соблюдены балансы по всем строкам и столбцам;
2) число заполненных клеток равно: m + n -1 = 6;
3) из заполненных клеток (или их части) нельзя образовать ни
одного замкнутого цикла.
Стоимость перевозок, соответствующая полученному опорному плану, уменьшается:
Z = 1·90 + 3·30 + 2·10 + 1·70 + 3·20 + 1·20 = 250 (тыс. руб.), т. е. новый опорный план лучше (дешевле) предыдущего.
Выясним, оптимален ли полученный план, с помощью метода потенциалов повторяя весь ход рассуждений, начиная с пункта 1.
Вычисляем новые потенциалы поставщиков и потребителей с помощью системы уравнений,
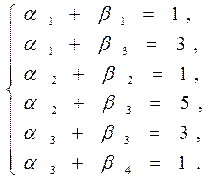
Ответ.Оптимальный план перевозок:
x11= 90; x13 = 30; x21 = 10; x22 = 70; x33 = 20; x34 = 20.
Расходы по его осуществлению минимальны и составляют Zmin = 350 тыс. руб.
Замечание. Количество таблиц при решении транспортной задачи может оказаться любым. Это зависит от того, насколько первый опорный план окажется близким к оптимальному. Может случиться, что первая же таблица будет соответствовать оптимальному плану. Это устанавливается методом потенциалов.
Транспортная задача всегда имеет оптимальное решение (один или несколько опорных оптимальных планов).
Задание к практическому занятию:
Базовый уровень:
Задание 1
В транспортной задаче, где запасы поставщиков описываются вектором А(50;70), потребности – вектором В (30;40;50), а стоимость перевозки единицы груза от поставщиков потребителям задана матрицей
Д =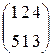 
, найти общую стоимость допустимого плана перевозок,
полученного по методусеверо-западного угла.
Ответ: 250
Задание 2
В транспортной задаче, где запасы поставщиков описываются вектором А(50;70), потребности – вектором В (35;50;35), а стоимость перевозки единицы груза от поставщиков потребителям задана матрицей
Д = 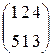, найти общую стоимость допустимогоплана перевозок,
полученного по методу северо-западного угла.
Ответ: 1)170
Задание 3
В транспортной задаче, где запасы поставщиков описываются вектором А(60;60), потребности – вектором В (35;50;35), а стоимость перевозки единицы груза от поставщиков потребителям задана матрицей
стоимость оптимального плана перевозок равна:
Д = 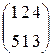, найти общую стоимость оптимального плана перевозок,
Ответ: 1) 120
Повышенный уровень:
Задание 4. Решить методом потенциалов транспортные задачи (табл. 5).
Таблица5. Варианты задания
| Вариант | Задача | Вариант | Задача | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Задание 5. Решить методом потенциалов транспортные задачи с ограничениями на пропускную способность (табл. 6).
Таблица 6. Варианты задания
| Вариант | Задача | Вариант | Задача | ||||||||||||||||||||||||||||||||||||||||||||||||||
x21£500, x44³500
| x21£500, x44³1000
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
x21£25, x32³20
| x42£50, x24³50
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
x23£30, x32³30
| x44£100, x23³50
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
x33£100, x42³100
| x43£50, x21³100
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
x32£100, x43³100
| x11£20, x33³30
|
Вопросы для самостоятельной работы
Базовый уровень:
1. Чем отличается постановка транспортных задач от других ЗЛП?
2. Перечислите и охарактеризуйте основные методы построения опорного плана.
3. В чем суть метода потенциалов для решения транспортных задач?
Повышенный уровень:
4. Дайте экономическую интерпретацию метода потенциалов.
5. Можно ли решать транспортные задачи графическим или симплексным методами?
Задание для самостоятельной работы:
Базовый уровень:
Имеются три пункта поставки однородного груза 
и пять пунктов 
потребления этого груза. На пунктах 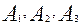находится груз соответственно в количестве 
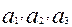тонн. В пункты 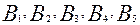требуется доставить соответственно 
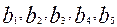тонн груза. Затраты на перевозку 1 тонны груза между пунктами поставки и потребления приведены в матрице Д (в рублях).
,
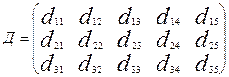где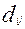 
– есть стоимость в рублях перевозки 1 тонны груза от поставщика с номером 
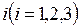к потребителю с номером 
.
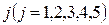Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты на перевозки были минимальными.
Поставить задачу и решить методом потенциалов.
3.1.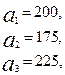 
.
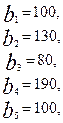
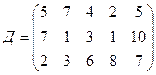3.2.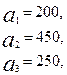 
.
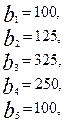
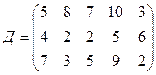3.3.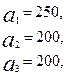 
.
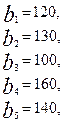
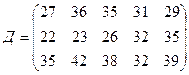3.4.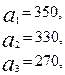 
.
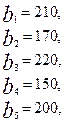
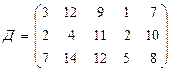3.5.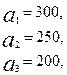 
.
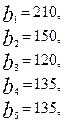
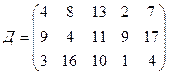3.6.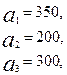 
.
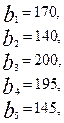
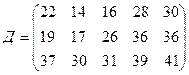3.7.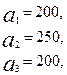 
.
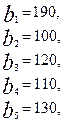
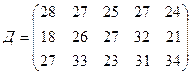3.8.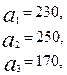 
.
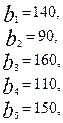
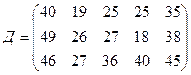3.9.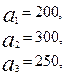 
.
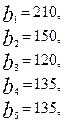
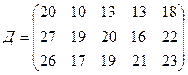3.10.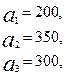 
.
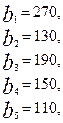
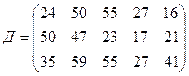3.11.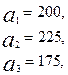 
.
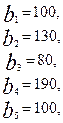
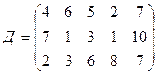3.12.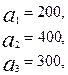 
.
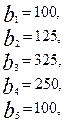
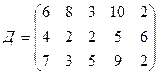3.13.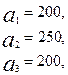 
.
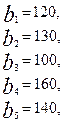
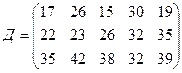3.14.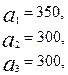 
.
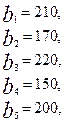
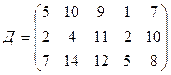3.15.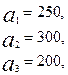 
.
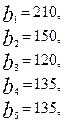
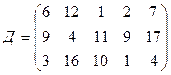3.16.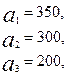 
.
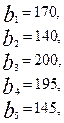
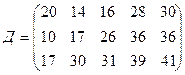3.17.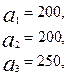 
.
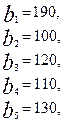
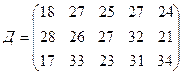3.18.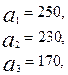 
.
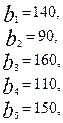
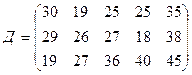3.19.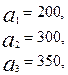 
.
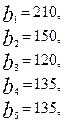
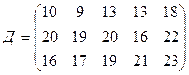3.20.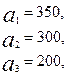 
.
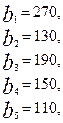
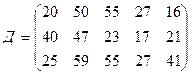3.21.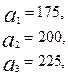 
.
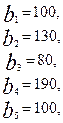
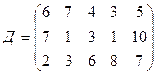3.22.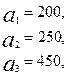 
.
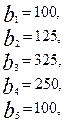
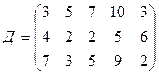3.23.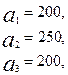 
.
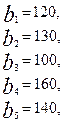
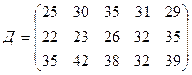3.24.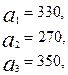 
.
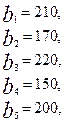
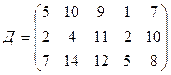3.25.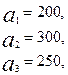 
.
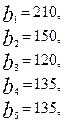
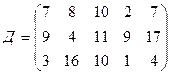3.26.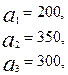 
.
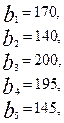
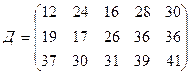3.27.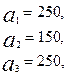 
.
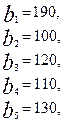
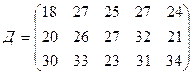3.28.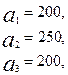 
.
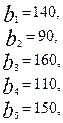
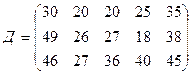3.29. . 
.
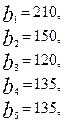
3.30.
.
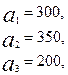
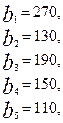
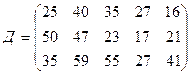