Передаточные функции фильтров
В общем виде алгоритм синтеза ARC- фильтров сводится к следующему:
· формируются требования к его амплитудной частотной характеристике (АЧХ), т.е. устанавливаются граничные частоты полос пропускания и задерживания, максимальное и минимальное значения АЧХ в полосе пропускания, максимально допустимое значение АЧХ в полосе задерживания;
· по требованиям к АЧХ синтезируется передаточная функция фильтра в виде произведения функций не выше 2-го порядка;
· производится анализ модуля синтезированной комплексной функции передачи в частотной области с целью проверки удовлетворения требованиям к АЧХ;
· каждая из функций 1-го и 2-го порядка реализуется тем или иным активным звеном на основе, как правило, операционных усилителей;
· звенья подключаются каскадно, обеспечивая тем самым реализацию произведения передаточных функций 1 -го и 2-го порядка и формируя схему фильтра;
· осуществляется физическая реализация фильтра с последующим экспериментальным исследованием его АЧХ с целью проверки удовлетворения требованиям.
При этом все расчеты базируются, как правило, на расчете нормированного фильтра прототипа низких частот (НЧП), с последующим переходом к реальному фильтру того или иного типа.
В качестве аппроксимирующих функций нашли широкое применение полимиальные и дробно рациональные – эллиптические: Баттерворта, Чебышева;
Если известны координаты нулей и полюсов синтезируемого фильтра, то передаточную функцию можно записать так:
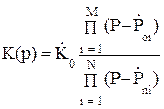 , (9.19)
, (9.19)
где К0 – нормирующий постоянный коэффициент; M – количество нулей; N – количество полюсов; P – комплексная частота.
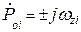 ;
; 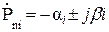 – нули и полюсы.
– нули и полюсы.
При этом нули всегда мнимые, а полюсы комплексно-сопряженные и/или действительные отрицательные. Если в формуле (9.19) раскрыть попарно скобки, группируя множители с комплексно-сопряженными нулями и полюсами, то получим:
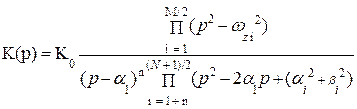 , (9.20)
, (9.20)
здесь n = 0 , если N – четное и N = 1, если N – нечетное.
Формула (9.20) записана для нормированного прототипа ФНЧ.
Отсюда следует, что с учетом каскадного представления ARC- фильтров, передаточная характеристика отдельного звена, в общем виде будет выглядеть так:
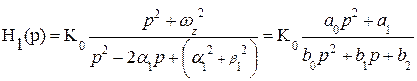 , (9.21)
, (9.21)
здесь b0 =1; b1 = -2α1 ; b2 = ( 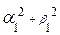 ), а0 =1: а1 =
), а0 =1: а1 = 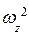 .
.
При этом 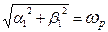 частота полюса звена фильтра;
частота полюса звена фильтра;
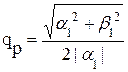 - называется добротностью полюса;
- называется добротностью полюса;
ωz – называется резонансной частотой нуля или частотой режекции.
Для звена ФНЧ первого порядка а0 = b0 = 0 ; b2 = 1, тогда получим:
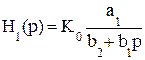 (9.22)
(9.22)
Реализация фильтров в виде каскадного соединения звеньев, не выше второго порядка, позволяет получить фильтры с низкой чувствительностью.
9.8 Преобразование частот
Как уже указывалось, расчет ARC – фильтров осуществляется на основе ФПНЧ и при его расчете используют нормированные частоты, а не реальные. Причем, переход к реальным частотам может быть осуществлен на последнем этапе, т.е. этапе реализации. Нормирование частоты и её трансформация позволяет свести характеристики ФНЧ, ФВЧ ППФ, ПЗФ к характеристикам эквивалентного ФПНЧ.
АЧХ ФПНЧ определена на нормированной оси частот так, что граничная частота ПП Ωn = 1, а граничная частота полосы задерживания Ωn>1. В качестве нормирующей частоты для ФНЧ и ФВЧ выбирается граничная частота полосы пропускания реального фильтра ωn.
Для ППФ и ПЗФ – центральная частота полосы пропускания ω0 = 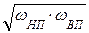 . Формулы для вычисления нормированных частот синтезируемого фильтра и его ФПНЧ приведены в таблице 9.6.
. Формулы для вычисления нормированных частот синтезируемого фильтра и его ФПНЧ приведены в таблице 9.6.
Таблица 9.6
| Тип | НЧ прототип | Синтезируемый фильтр |
| ФНЧ | 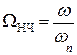 ; ; 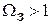 | 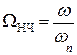 ; ; 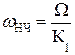 ; ; 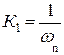 |
| ФВЧ | 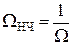 , Здесь происходит трансформация частот , Здесь происходит трансформация частот 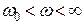 В нормированные В нормированные 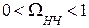 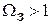 | 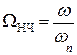 ; ; 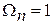 ; ; 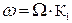 ; ; 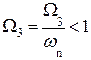 |
| ППФ | 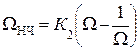 здесь происходит трансформация частот здесь происходит трансформация частот 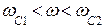 В нормированные В нормированные 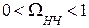 | 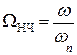 ; ; 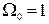 ; ; 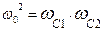 ; ; 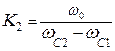 ; ; 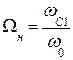 ; ; 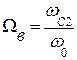 ; ; 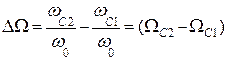 ; ; 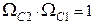 нормированные частоты ППФ связаны с нормированными частотами ФПНЧ нормированные частоты ППФ связаны с нормированными частотами ФПНЧ 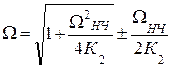 |
Для расчетов ФПНЧ требуется знание трех параметров:
aп, aз – затухание в полосе пропускания и запирания, и частоту заграждения ΩЗ . При этом для ППФ и ПЗФ в качестве ΩЗФПНЧ выбирается большая из ΩЗ1, ΩЗ2.
Координаты нулей и полюсов ФПНЧ также не обходимо пересчитать в соответствующие нули и полюса синтезируемого фильтра (ФВЧ, ППФ, ПЗФ). Формулы пересчета представлены в таблице 9.7.
Таблица 9.7
| Тип | Нули | Полюсы |
| ФВЧ | 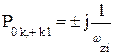 , где i = 1,2,… , где i = 1,2,… 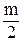 , k = 1,3,5,…, m -1 , k = 1,3,5,…, m -1 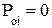 , i = m+1, m+2, ….., n , i = m+1, m+2, ….., n | 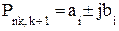 , где , где 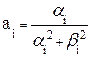 ; ; 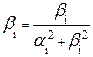 , где i = 1,2,… , где i = 1,2,… 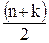 , k=0 (n - четное), к=1 (n- нечетное) k = 1,3,5,…, n -1 (n - четное) k = 1,2,4,6…, n -1 (n - нечетное) , k=0 (n - четное), к=1 (n- нечетное) k = 1,3,5,…, n -1 (n - четное) k = 1,2,4,6…, n -1 (n - нечетное) |
| ППФ | 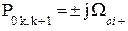 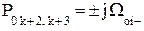 , где , где 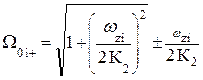 i = 1,2,… i = 1,2,… 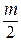 , k = 1,5,9,…, 2m -3, , k = 1,5,9,…, 2m -3, 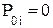 , где i = 2m+1, 2m+2, ….., n+m ω – частоты нулей ФПНЧ , где i = 2m+1, 2m+2, ….., n+m ω – частоты нулей ФПНЧ | 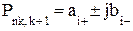 ; ; 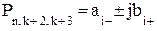 , где , где 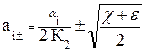 ; ; 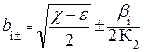 ; ; 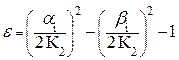 ; ; 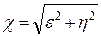 , где , где 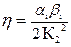 где i = 1,2,… где i = 1,2,… 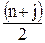 , j=0 (n - четное), j=1 (n- нечетное) k = 1,5,9,…, 2n -3 (n - четное) k = 1,3,7,11…, 2n -3 (n - нечетное) , j=0 (n - четное), j=1 (n- нечетное) k = 1,5,9,…, 2n -3 (n - четное) k = 1,3,7,11…, 2n -3 (n - нечетное) |
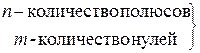 в ФПНЧ в ФПНЧ |
Данные формулы получены на основе правил замены комплексной переменной p при переходе от ФПНЧ к другим видам фильтров Каждый полюс или нуль при переходе от ФПНЧ к ППФ или ПЗФ порождает два полюса или два нуля, так что порядок синтезируемого фильтра по сравнению с прототипом увеличивается в два раза. При пересчете оказывается что для ФВЧ и ПЗФ количество нулей равно количеству полюсов, для ППФ число нулей на n – m меньше числа полюсов. Для ФВЧ и ППФ появляются дополнительные нули pok = 0, количество которых равно n –m для ФПНЧ
