Упрощение системы линейных неравенств, описывающих область допустимых изменений параметров. Получение решения систем линейных неравенств

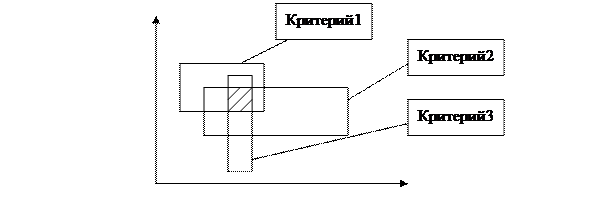
При оптимизации должны выполняться все критерии. В результате остается только заштрихованная область. Таким образом, появляется масса лишних неравенств, которые должны быть удалены.

Если проводим оптимизацию по критерию 1, то нужно учитывать все критерии, все ограничения, в связи с этим система уравнений имеет очень большой порядок. Поэтому оптимизацию следует проводить после исключения лишних неравенств.

Исходная система неравенств имеет вид:

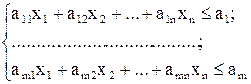
при x_i ≥ 0.

Это ограничения для всех критериев.

Обычно задачу сводят к однородной системе ограничений, то есть правая часть нули.

Введем дополнительную переменную x_n+1 и перенесем ее влево:

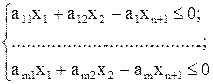
x_i ≥ 0, .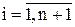

Все неравенства при этом должны быть со знаком « ≤ ».

Решив эту систему, положим x_n+1=1.

Вернемся к исходной задаче. Теперь решаем систему:

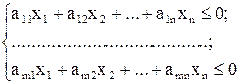
Решение проводится с помощью преобразования ряда таблиц. Для этого вводятся обозначения:

Т₁¹ – единичная матрица размером n×n;

T₂¹ – транспонирование исходной матрицы.

Здесь верхний индекс – это номер итерации (шага), нижний индекс – разбиение матрицы Т на две части.

Тогда матрицу Т на первой итерации можно представить в виде:

Пример1. Исключение неравенств

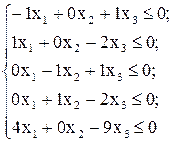
Если первое уравнение умножить на 1, а второе – на 5 и сложить их, то получится пятое уравнение. Следовательно, пятое уравнение лишнее, его нужно исключить.

Исходную систему можно представить в виде матрицы Т следующим образом:

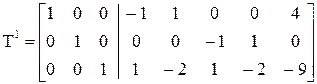
Если в матрице Т₂¹ появляются столбцы, содержащие нули и отрицательные элементы, то эти столбцы лишние.

Если появляется столбец строго положительный, то система несовместна, то есть решения нет.

Алгоритм

1. В правой части (то есть в матрице Т₂¹) находится основной столбец – тот столбец, в котором есть положительные элементы.

2. Ищем допустимые пары строк – это пары строк, пересекающие основной столбец по элементам с разными знаками.

3. Среди допустимых пар ищем уравновешенные пары. Для этого в матрице Т₁¹ нужно найти столбцы (столбец), пересекающие допустимую пару по нулевым элементам. И не существует строк, пересекающих подобные столбцы по нулевым элементам.

4. Формируем матрицу Т².

В рассматриваемом примере в качестве основного столбца берём крайний слева, то есть первый. 1-ая и 3-я строки – допустимая, уравновешенная пара.

Правило формирования Т²

Выписываются строки, пересекающие основной столбец по отрицательным элементам и нулям в любой последовательности, и выписывается строка равновесия. Строка равновесия формируется из уравновешенных пар путем умножения их на положительные коэффициенты такие, что на месте основного столбца получается нуль. Для повышения точности желательно все расчеты проводить в целых числах.

Основной столбец наделяется свойствами столбцов матрицы Т¹. Элементы основного столбца, отличные от нуля, заменяются на «-1».

В данном примере складываем первую и третью строки, в результате получаем матрицу Т²:

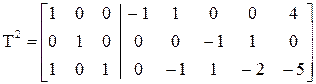
5. Для формирования матрицы Т³ будем искать в матрице Т² основной столбец (в примере это 2-ой столбец), допустимые пары (1-ая и 3-я строки). Эта же пара и уравновешенная.

6. Выписываем строки, пересекающие основной столбец по отрицательным элементам и нулям, а строку равновесия с единичными коэффициентами.

В примере поскольку основной столбец пересекает по отрицательному элементу 3-ю строку, то эту третью строку в матрице Т³ записываем на первое место. Вторую строку оставляем без изменений, а первую и третью строки складываем и записываем результат на место третьей строки:

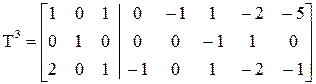
Здесь пятый столбец лишний, поэтому он исключается.

7. Формируем матрицу Т⁴: основной столбец третий.

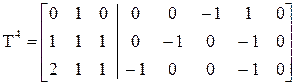
Допустимые, уравновешенные пары: 1,3 и 1,2.

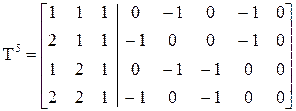
Выбрать основной столбец невозможно, строго положительного

столбца нет, значит, выписываем решение.

Решение системы можно представить в виде:

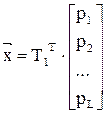, где L – число строк последней матрицы,

р_i ≥ 0.

Для примера решение будет иметь вид:

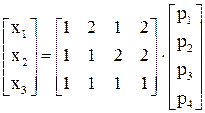
Решение можно представить в виде системы (в скалярной форме):

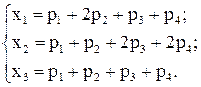
При р₁ = 1, р₂ = 1, р₃ = 1 и р₄ = 1 получим х₁ = 6, х₂ = 6, х₃ = 4.

При данных ограничениях х_i эта система выполняется.

Далее выражения для х_i подставляются в целевую функцию, а в качестве ограничения берется уравнение x_n+1=1. Затем находится решение полученной системы.

УСТОЙЧИВЫЕ АДАПТИВНЫЕ МЕТОДЫ ОЦЕНИВАНИЯ параметров НА ОСНОВЕ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ.(АОИ)

Использование методов математической статистики позволяет находить по результатам выборочных измерений оценки искомых параметров математического ожидания, дисперсии и других числовых характеристик случайных величин.

Однако, поскольку оценки искомых параметров являются случайными величинами, то нельзя точно указать величину ошибки в определении этих параметров. Но если известен закон распределения результатов измерений, то оказывается, возможным сделать по этой ошибке суждения вероятностного характера, например, оценить доверительный интервал, который «накрывает» с известной вероятностью Р неизвестное истинное значение искомого параметра .Но знание интервала не увеличивает точность оценок, хотя и является важной дополнительной информацией. Для этого необходимо применять специальные методы. Одним из таких методов является метод максимального правдоподобия, основанный на предположении, что известен закон распределения измеряемых случайных величин, зависящий от искомых параметров.