Уточнение корней методом половинного деления

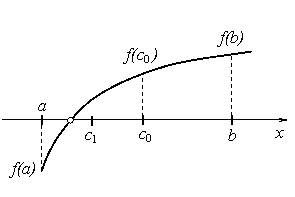
Рисунок 2 – Метод половинного деления.

Считаем, что отделение корней уравнения (1) проведено и на отрезке 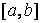расположен один корень, который необходимо уточнить с погрешностью e. В качестве начального приближения корня принимаем середину этого отрез

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КП

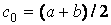ка: (рис. 2). Затем исследуем значение функции 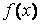на концах отрезков 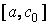и 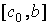. Тот из отрезков, на концах которого 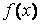принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка 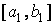(на рис. 2 это отрезок 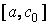). Вторую половину отрезка 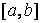, на которой 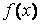не меняет знак, отбрасываем. В качестве следующего приближения корня принимаем середину нового отрезка 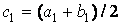и т.д. Таким образом, k-е приближение вычисляется как

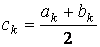. (2)

После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после k итераций в 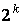раз:

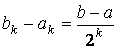. (3)

Прекратить итерационный процесс следует, когда будет достигнута заданная точность, т.е. при выполнении условия

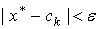. (4)

Поскольку корень 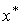принадлежит отрезку 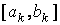, а 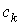– середина этого отрезка, то величина 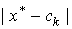всегда будет меньше половины длины отрезка 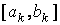(см. рис. 2), т.е.

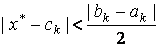. (5)

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КП

Следовательно, условие (4) будет выполнено, если

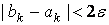. (6)

Таким образом, итерационный процесс нужно продолжать до тех пор, пока не будет выполнено условие (6).

В отличие от большинства других методов уточнения, метод половинного деления сходится всегда, т.е. обладает безусловной сходимостью. Кроме этого он чрезвычайно прост, поскольку требует лишь вычисления значений функции 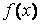и, поэтому применим для решения любых уравнений.

Однако метод половинного деления довольно медленный. С каждым шагом погрешность приближенного значения уменьшается в два раза, т.е.

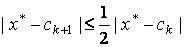, (7)

поэтому данный метод является методом с линейной сходимостью.

Вычислим количество итераций N, требуемое для достижения заданной точности e. Пользуясь выражением (3) можно выяснить для каких значений k будет выполнено условие (6), и взять в качестве N наименьшее из таких k:

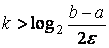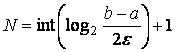, , (8)

где 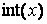– целая часть числа x. Например, пр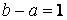и и 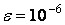получим .

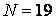Ø Замечание. При реализации метода следует учитывать, что функция 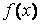вычисляется с некоторой абсолютной погрешностью 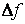. Вблизи корня значения функции 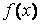малы по абсолютной величине и могут оказаться сравнимы с погрешностью ее вычисления. Другими словами, при подходе к корню мы можем попасть в полосу шумов 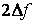и дальнейшее уточнение корня окажется невозможным. Поэтому целесообразно задать ширину полосы шумов и прекратить итерационный процесс при попадании в нее. Ес

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КП

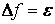ли принять , то итерационный процесс можно завершать, когда значение функции 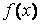после k-й итерации станет меньшим по модулю e., т.е.

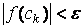. (9)

Также необходимо иметь ввиду, что при уменьшении интервала 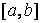увеличиваются погрешности вычисления его длины 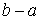за счет вычитания близких чисел[1, стр 185].