Идентификация, функционалы качества и алгоритмы отыскания их оптимальных значений

Процессы, протекающие в объектах и системах, могут быть математически описаны некоторым оператором W_o (a, x, t) (В дальнейшем иногда используем сокращенное обозначение оператора, без указания параметров), где а (a₁,..., a_i ..., a_n) — вектор параметров оператора; a_i — i-й параметр; x — входной сигнал; t — время.

Например, процесс y на выходе объекта (рис. 13) может быть описан дифференциальным, интегральным или разностным уравнениями, передаточной, весовой или переходной функциями, частотными характеристиками и др. В конкретных случаях формальный вид оператора W_o выбирается из соответствующего математического языка с учетом адекватности последнего, а также конструктивности и удобства.

Если объект линейный, то оператор W_o не зависит от входного сигнала х и имеет вид W_o (а, t). Если структура и параметры объекта стационарны, то оператор не зависит от времени, т. е. W_o (а, х). Если объект линеен и стационарен, то оператор W_o определяется только вектором параметров а(a₁,..., a_i ..., a_n).

Математическая модель Ŵ_o (â, х, t), описывающая процессы на выходе объекта при известных х и t и полученная в результате решения сформулированной ниже задачи идентификации, является оценкой оператора W_o аналогично â _i, — оценкой i-го параметра объекта.

При техническом решении задачи идентификации необходимо учесть имеющиеся ограничения, обусловленные условиями работы объекта, общей целью идентификации и качеством решения задачи. Так, например, если известно, что на объект поступают воздействия х(t), принадлежащие некоторому множеству воздействий, то модель Ŵ_o (â, х, t) должна с требуемой точностью описывать процессы на выходе объекта, когда на его вход поступают воздействия, принадлежащие множеству Ω _x.

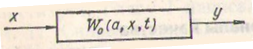
Рис. 13. Структурная схема объекта идентификации.

Если объект идентифицируют с целью построения системы оптимального управления, то важно получать возможно более точные оценки тех параметров, от которых наиболее существенно зависит величина меры оптимальности управления, и, очевидно, нет необходимости в точном определении оценки тех параметров, от которых мера оптимальности управления слабо или совсем не зависит. Таким образом, идентификация в задачах измерения и оптимального управления несколько различна.

Точные математические модели объекта обычно достаточно сложны. На практике нет необходимости в определении точных моделей. Поэтому обычно оценку Ŵ_o ищут в определенном классе операторов.

Информация о структуре и параметрах объекта содержится обычно в его выходном сигнале у (t). Проводником этой информации являются входные сигналы. Однако не все входные сигналы позволяют выявить природу исследуемого объекта. Например, сигнал в виде постоянного напряжения не может выявить величину постоянных времени объектов, обладающих инерционными свойствами. Поэтому для исследования определенных свойств объекта на его вход необходимо подавать соответствующие сигналы. Те входные сигналы, которые позволяют выявить интересующее нас свойство объекта, будем называть информативными.

Наиболее информативным сигналом для определения общих свойств объектов является сигнал типа «белый шум», так как содержит всю гамму частотного спектра, т. е, класс сигналов «белый шум» является наиболее общим классом входных сигналов при идентификации. Однако, с практической точки зрения, входной сигнал, на основе которого производится идентификация, должен быть не менее информативным, чем сигналы, принадлежащие множеству Ω _x возможных входных сигналов объекта.

Таким образом, задача идентификации состоит в следующем.

Имеется некоторый объект, описываемый оператором W_o (a, x, t) и принадлежащий некоторому классу операторов Ω_Wo. На его вход поступают сигналы х, принадлежащие некоторому множеству сигналов Ω_x. Необходимо выбрать некоторый оператор Ŵ_o (а, х, t) из множества операторов Ω_Ŵo, который для того же класса входных сигналов Ω_x будет достаточно близким к оператору W_o (а, x, t), т. е. будет описывать процессы на выходе объекта с требуемой точностью.

Класс операторов Ŵ_o обычно задается и, как правило, является более узким, чем Ω_Wo. Для исследования, например, некоторых свойств нелинейных систем иногда применяют линейные модели или при исследовании сложных систем высокого порядка применяют модели более низкого порядка.

Таким образом, задача идентификации объектов есть не что иное, как задача аппроксимации неизвестного оператора ‚ W_o Є Ω_Wo оператором Ŵ_o, выбранным обычно из известного класса операторов Ω _Ŵo, для определенного класса входных воздействий x Є Ω x. Мера близости операторов W_o и Ŵ_o конструируется с учетом требований к оценке Ŵ_o.Оператор Ŵ_o (а, x, t) является решением задачи идентификации.

Во многих случаях идентификации не все входные сигналы объекта являются полезными для определения его математической модели Ŵ_o. Те из них, которые не поддаются измерению и от которых мы хотим избавиться, представляют собой помехи и могут иметь как детерминированный, так и стохастический характер. Наличие случайных помех приводит к случайному характеру полученной оценки Ŵ_o,и тогда предъявляют некоторые требования к ее статистическим характеристикам. Такие требования состоят в несмещенности , эффективности, состоятельности и достаточности оценок Ŵ_o. В этом случае в постановке задачи идентификации также учитывают требования к статистическим характеристикам оценки Ŵ_o.

Оценки, удовлетворяющие необходимым требованиям, ищутся обычно на основе определенных, специальным образом выбранных функционалов качества I (ε, x, Т), где Т - интервал времени идентификации. К сожалению, нет общего правила выбора функционалов качества, и эта задача имеет неоднозначное решение. Известно только общее требование к таким функционалам, состоящее в их адекватности для решения задачи идентификации. Под этим будем понимать следующее: некоторое значение I* (например, экстремальное значение I) должно говорить о том, что найденная оценка Ŵ_o оператора W_o удовлетворяет предъявленным к ней требованиям. Значение I обычно зависит от значения параметра ȃ, полезного входного сигнала и помехи. Однако не все выражения, зависящие от указанных аргументов, могут быть использованы при решении задачи идентификации. Будем называть I «правильно построенным» функционалом, если для него может быть указан метод определения оценки Ŵ_o (например, нахождение I*), при этом он должен исключить влияние помех на результат идентификации.

На практике преимущественно используют такие функционалы I, которые позволяют относительно просто получить интересующие оценки (например, функционал I в виде среднего квадрата отклонения).

Если функционал качества I является детерминированным выражением, то оценки ε_i найденные на его основе, удовлетворяют вышеуказанным требованиям. Если в качестве функционала выбрать другой функционал I ', связанный с I преобразованием I ' = LI, где L - некоторый оператор, допускающий обратное преобразование I =L ˉ I ', то ясно, что и на основе I ' можно найти Ŵ_o, удовлетворяющее упомянутым требованиям. Вообще существует целый класс функционалов качества, на основе которых можно получить идентичные оценки оператора W_o.

При наличии помех в функционале качества I необходимо предусмотреть соответствующие операции, уменьшающие случайный характер самого функционала, т. е. превращающие его в инвариантный по отношению к помехам. Обычно в качестве таких операций применяют усреднение по времени или по ансамблю. В случае линейных объектов можно наметить один путь формирования инвариантных по отношению к помехам функционалов качества. Функционал I может быть сформирован, например, следующим образом:

I=E f [Ŵ_o,x,n] (14.1)

где Е - оператор усреднения; f - некоторая выпуклая функция.

С учетом линейности оператора Е выражение (1) запишем следующим образом:

I= E f ₁ [Ŵ_o , x] + E f ₂ [Ŵ_o , x , n] + E f ₃ [Ŵ_o , n] (14.2)

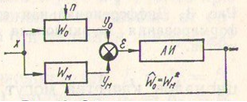
Рис. 14 Общая схема системы идентификации с моделью обьекта. W_m-оператор модели; АИ – алгоритм идентификации.

Оператор усреднения Е снимает неопределенность, вносимую функциями f ₂ и f ₃, в функционале I. В некоторых случаях (например, в задачах у идентификации линейных объектов при некоррелированных х и n) удается выбрать такую функцию, что второй и третий члены в выражении (2) становятся равными нулю.

Различным функциям f в функционале I соответствует различное соотношение между полезным сигналом (первый член выражения (2)) и помехой (остальные члены выражения (2)). Поэтому выбор f необходимо производить так, чтобы отношение сигнал/помеха в функционале I было удовлетворительным. От вида функционала при замкнутых алгоритмах идентификации (при компенсационных методах идентификации) также зависит сходимость и качество процесса идентификации.

В случае применения разомкнутых алгоритмов идентификации (при не компенсационных аналитических методах идентификации), помимо указанного пути формирования I , возможно применение критериев качества, построенных на известных стратегиях Байеса, максимума апостериорной вероятности, максимума функции правдоподобия, минимаксной стратегии и др. Но для применения указанных стратегий необходимо знать статистические характеристики помех. В этом заключается основной недостаток указанных стратегий. Функционал вида (l) содержит идею исследования характеристик помехи в процессе идентификации.

Широко применяют системы идентификации с моделью объекта (рис.14). Некоторое значение W^*_m оператора модели W_m принимают согласно критерию оптимальности в качестве оценки оператора объекта W_o , т.е. W^*_m=Ŵ_o

При отсутствии помех функционал качества идентификации может быть сформулирован на основе разности ε выходных сигналов объекта у_о, и модели у_m. При наличии помех о совпадении операторов модели и объекта можно судить по разности части сигнала объекта, зависящей от полезного входного сигнала, и сигнала модели. Отсюда вытекает задача подавления помехи в результате идентификации.

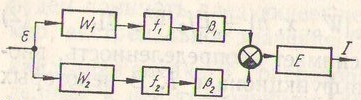
Рис. 15. Дифференциальная схема формирования функционала качества.

В случае стационарных линейных объектов и стационарных некоррелированных х и n для формирования инвариантных функционалов качества могут быть применены идеи многоконтурных инвариантных систем. В частности, функционал I может быть образован в виде двух дифференциальных операторов по схеме рис. 15.

I= β₁E f₁ W_1ε — β₂ E f₂ W_{2 ε} (14.3)

где W ₁ , W ₂— некоторые операторы; f₁ и f₂ — некоторые выпуклые преобразования; β₁ и β₂ — коэффициенты.

Подставляя ε = у_о — у_m = (у_оx + у_om) — уm, получаем

I =β₁E f₁W_{1 (} у_о-у_{m )} - β₂ E f₂ W₂ ( у_оx-у_om )+β₁ E f₁ W₁ у_оn+β₂ E f₂ W₂ у_оn (14.4)

Учитывая, что у_оx = W_ox, у_оn= Wⁿ_on, у_m =W_m , где W_o — оператор объекта, преобразующий помеху n, из соотношении (4) получаем:

I= β₁E f₁W₁ ΔWx - β₂Ef₂W₂ ΔWx + β₁E f₁W₁ Wⁿ_on - β₂Ef₂W₂ Wⁿ_on ;

ΔW =W_o - W_m (14.5)

Выбирая в выражении (5) коэффициенты β₁, и β₂, удовлетворяющие следующему условию: β₁ / β₁ = (E f₂W₂ Wⁿ_on) /( Ef₁W₁ Wⁿ_on) (14.6)

получаем функционал качества, не зависящий от помехи n: 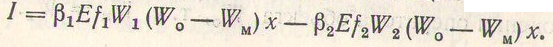. (14.7)

Таким образом, на выходе схемы, изображенной на рис. 15, получаем информацию, зависящую только от полезного сигнала x и от рассогласования операторов объекта и модели.

На практике часто принимают f₁ = f₂ = f₃ (обычно квадраторы). Тогда из выражения (7) получаем

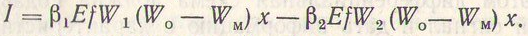(14.8)

Для информативности функционала I операторы W₁, и W₂ должны удовлетворять некоторым требованиям.

Из выражения (5) видно, что если W₁ = W₂ = 0, то при любых значениях β₁ и β₂ функционал I не зависит от помехи. Однако в таком случае I = 0 и является неинформативным.

Пусть W₁ = W₂ (в предположении, что f₁ = f₂ = f). Тогда на основе выражения (6) получаем β₁ = β₂ = β. Но при этом, как видно из соотношения (8), опять I = 0.

Пусть W₁ = bW₂; b = const. Тогда из выражения (6) (β₁ = b β₂) и при этом также I = 0.

Пусть в областях существования х и n (например, в частотных спектрах х и n) E f W₁x= E f W₂x. Нетрудно заметить, что и в этом случае I=0. Таким образом, область неинформативных операторов состоит из W₁, и W_2, для которых справедливы следующее соотношения:

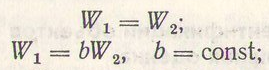(14.9)

E f W₁= b E f W₂ ; b = const. по отношению к n и x.

При выборе W₁, и W₂ из областей, близких к (9), получаем плохие по чувствительности функционалы качества.

С точки зрения максимальной чувствительности функционала I, как видно, например, из выражения (8) желательно, чтобы E f W₂(W_o — W_m)х=0 (или E f W₁(W_o — W_m)х= 0), т. е. чтобы W₂ представлял некоторый фильтр-пробку для полезных выходных сигналов у_оx и у_om.

По физической природе операторы W₁ и W₂ могут быть самые различные: нелинейные звенья, модуляторы и др. Наиболее известны и удобны для реализации W₁ и W₂ виде двух частотных фильтров с различными по форме частотными характеристиками, достаточно хорошо описанными, например, в работе.

Применение функционалов I с использованием дифференциальных операторов позволяет исключить из результата идентификации даже ту часть спектра помехи, которая совладает со спектром полезного сигнала. Для нестационарных помех необходима адаптация какого-нибудь из коэффициентов β₁ или β₂ с целью обеспечения условия (6). Для достижения такой пели можно применить алгоритм, построенный также на идее дифференциальных операторов. При этом дифференциальная схема должна подавить полезный сигнал и дать информацию о характеристиках помехи, на основе которой можно будет перестраивать β₁ и β₂.

Во многих случаях для получения инвариантных по отношению к помехам функционалов качества можно применять алгоритмы, основанные на корреляционных методах. Особо эффективно это в случае некоррелированных полезного сигнала и помехи.

Функционалы качества должны быть адекватными для решения задачи идентификации. Существенным моментом является организация движения в системе идентификации к оптимальному (экстремальному) значению функционала качества. В случае унимодальных функционалов качества поиск их экстремальных значений может быть осуществлен методами градиента, наискорейшего спуска, Гаусса - Зейделя, стохастической аппроксимации и случайным поиском [52, 115, 154]. Техническая реализация указанных алгоритмов приводит к различным системам идентификации.