Метод простых итераций
Рассмотрим более общий итерационный метод уточнения корней. Представим исходное уравнение 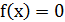 в виде
в виде 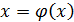 .
.
Пусть нам известно начальное приближение к корню 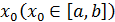 . Подставив его в правую часть уравнения
. Подставив его в правую часть уравнения 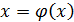 получим новое приближение
получим новое приближение 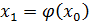 , затем аналогичным образом получим
, затем аналогичным образом получим 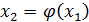 и так далее,
и так далее, 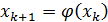 .
.
Оказывается, что при определенных свойствах функции 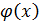 последовательность
последовательность 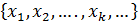 , определяемая по формуле
, определяемая по формуле 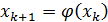 , сходится к корню уравнения
, сходится к корню уравнения 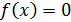 .
.
Теорема.Пусть функция 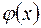 определена и дифференцируема на отрезке [a;b], причем все ее значения
определена и дифференцируема на отрезке [a;b], причем все ее значения 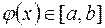 . Тогда, если выполняется условие
. Тогда, если выполняется условие 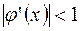 при : a<x<b
при : a<x<b
1) процесс итерации 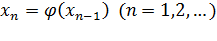 сходится не зависимо от начального значения
сходится не зависимо от начального значения 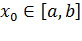 ;
;
2) предельное значение 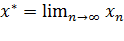 является единственным корнем уравнения
является единственным корнем уравнения 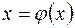 на отрезке
на отрезке 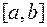 .
.
Рассмотрим графически процесс получения приближений в методе простых итераций (рис.5). Необходимо отыскать точку пересечения кривой 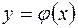 и прямой
и прямой 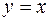 .
.
На рисунке 5, (а) изображена некоторая кривая 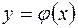 , которая может представлять собой любую функцию, но сейчас для нас важно то обстоятельство, что производная этой функции в окрестности корня
, которая может представлять собой любую функцию, но сейчас для нас важно то обстоятельство, что производная этой функции в окрестности корня 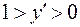 . Пусть
. Пусть 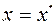 - корень уравнения, который, естественно, предполагается неизвестным. Выберем начальное приближение в точке
- корень уравнения, который, естественно, предполагается неизвестным. Выберем начальное приближение в точке 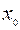 . Следующее приближение
. Следующее приближение 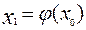 . Для того, чтобы отобразить
. Для того, чтобы отобразить 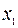 на графике можно провести через точку
на графике можно провести через точку 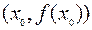 прямую, параллельную оси
прямую, параллельную оси 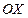 , до пересечения с прямой
, до пересечения с прямой 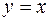 , а затем в точке пересечения этих прямых опустить перпендикуляр на ось
, а затем в точке пересечения этих прямых опустить перпендикуляр на ось 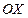 , который и отметит положение точки
, который и отметит положение точки 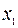 . Аналогично получаются все последующие приближения. Из рисунка видно, что они сходятся к корню. Напомним, что для рассмотрения мы взяли функцию, производная которой
. Аналогично получаются все последующие приближения. Из рисунка видно, что они сходятся к корню. Напомним, что для рассмотрения мы взяли функцию, производная которой 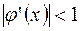 .
.
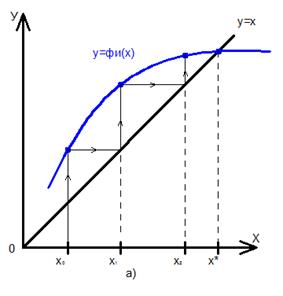
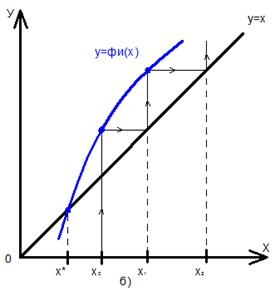
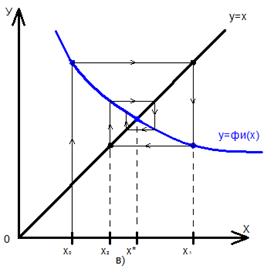
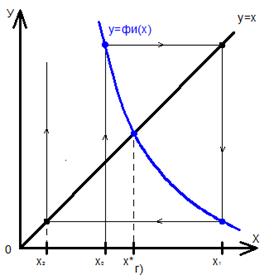
Рисунок 5. Метод простых итераций: а) односторонний сходящийся процесс; б) односторонний расходящийся процесс; в) двухсторонний сходящийся процесс; г) двухсторонний расходящийся процесс.
Рассмотрим теперь другую функцию 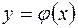 , производная которой отрицательна,
, производная которой отрицательна, 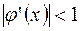 по абсолютному значению. Этот случай изображен на рисунке 5, в). Последовательные приближения также сходятся к корню, но на этот раз каждое последующее приближение находится с противоположной стороны от корня. В то время как в первом случае все последовательные приближения находились с одной стороны от корня.
по абсолютному значению. Этот случай изображен на рисунке 5, в). Последовательные приближения также сходятся к корню, но на этот раз каждое последующее приближение находится с противоположной стороны от корня. В то время как в первом случае все последовательные приближения находились с одной стороны от корня.
Наконец, рассмотрим случай, когда произвольная функции 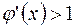 (рис. 5, б) и
(рис. 5, б) и 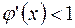 (рис. 5, г). В обоих случаях каждое последующее приближение отстоит дальше от корня, т.е. итерационный процесс расходится. Из сказанного выше можно предположить, что итерационный процесс сходится при условии, что производная
(рис. 5, г). В обоих случаях каждое последующее приближение отстоит дальше от корня, т.е. итерационный процесс расходится. Из сказанного выше можно предположить, что итерационный процесс сходится при условии, что производная 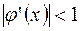 .
.
