Аналитическое выражение первого начала термодинамики
Значения удельных внутренней энергии и энтальпии простого тела однозначно определяются двумя независимыми переменными и могут быть представлены следующим образом:
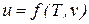 ;
;
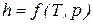 .
.
Изменения внутренней энергии и энтальпии простого тела, как функций состояния, в элементарных процессах являются полными дифференциалами и определяются соотношениями
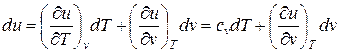 ; (1)
; (1)
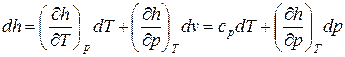 . (2)
. (2)
Для изохорного процесса ( 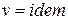 ) частная производная внутренней энергии по температуре равна истинной изохорной теплоемкости
) частная производная внутренней энергии по температуре равна истинной изохорной теплоемкости
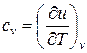 , (3)
, (3)
а для изобарного процесса ( 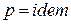 ) частная производная энтальпии по температуре равна истинной изобарной теплоемкости
) частная производная энтальпии по температуре равна истинной изобарной теплоемкости
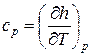 . (4)
. (4)
В результате подстановки выражений (1) и (2) в уравнение 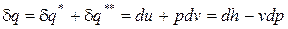 и разделения переменных получим:
и разделения переменных получим:
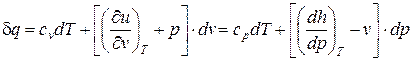 . (5)
. (5)
Данное соотношение (5) называется первым началом термодинамики для простых тел в аналитической форме.
Вопрос №8
Первое начало термодинамики для идеального газа.
Идеальный газ – система, которая подчиняется уравнению Менделеева-Клаперона: 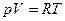 и внутренняя энергия системы зависит только от температуры
и внутренняя энергия системы зависит только от температуры 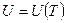 .
.
Первое начало термодинамики для простого тела: 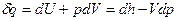 . Для идеального газа:
. Для идеального газа: 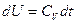 ,
, 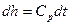 ,
, 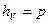 ,
, 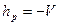 . Получим:
. Получим:
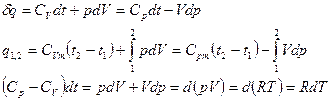
Получили закон Майера: 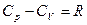 .
.
Универсальная газовая постоянная 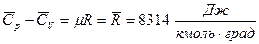 .
.
Разделим первое начало термодинамики на 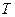 :
:
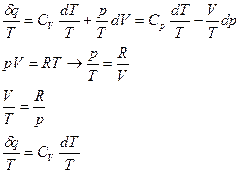
Вопрос №9
Энтропия 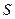 ,
, 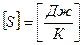 .
.
Удельная энтропия 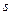 ,
, 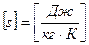 .
.

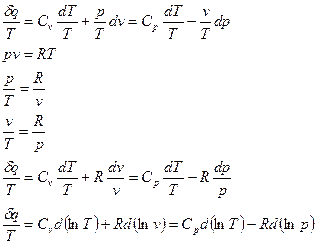
Энтропия, как и время, всё время возрастает. Только в изолированной системе энтропия может оставаться постоянной.
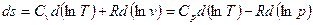
При давлении 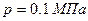 и температуре
и температуре 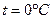 удельная энтропия
удельная энтропия 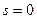 .
.
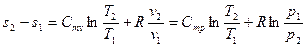 , где
, где 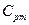 - вторая средняя теплоёмкость или логарифмическая теплоёмкость.
- вторая средняя теплоёмкость или логарифмическая теплоёмкость.
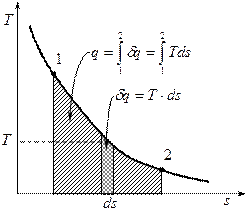 Так как
Так как 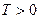 , то если энтропия растёт, то есть
, то если энтропия растёт, то есть 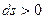 , то тепло подводится, то есть
, то тепло подводится, то есть 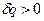 .
.
Уравнение, определяющее энтропию:
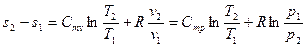
Вопрос №10
Адиабатный процесс- термодинамический процесс изменения состояния системы, при котором отсутствует теплообмен 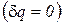 и в силу обратимости процесса энтропия остается величиной постоянной
и в силу обратимости процесса энтропия остается величиной постоянной 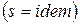 .
.
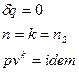 , показатель адиабатического процесса.
, показатель адиабатического процесса.

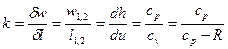
Первое начало термодинамики: 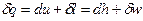 . Для идеального газа:
. Для идеального газа: 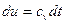 и
и 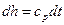 .
.
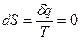
 Если
Если 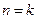 , то
, то 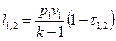 . Так как
. Так как 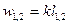 , то достаточно знать одну из работ, чтобы определить другую.
, то достаточно знать одну из работ, чтобы определить другую.
Для идеального газа: 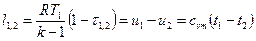 .
.
Изопотенциальный процесс.
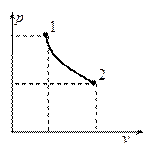
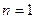
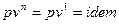
Так как 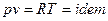 , то
, то  , следовательно, процесс будет также являться изотермическим.
, следовательно, процесс будет также являться изотермическим.

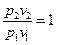
Для идеального газа:
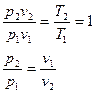
Первое начало термодинамики: 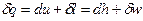 . Если процесс изотермический, то есть
. Если процесс изотермический, то есть  , следовательно
, следовательно 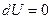 . Для идеального газа
. Для идеального газа  , тогда:
, тогда:
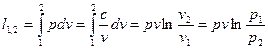 .
.
Изобарный и изохорный процессы.
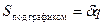
Если 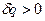 , то идёт процесс расширения.
, то идёт процесс расширения.
Изобарный процесс.
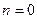
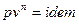
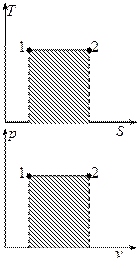
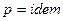
Так как 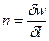 , то
, то 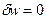 .
.
Для идеального газа:
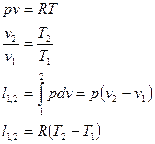
Первое начало термодинамики: 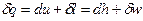 .
.
Для идеального газа:  и
и 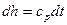
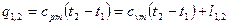 .
.
Изохорный процесс.
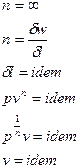
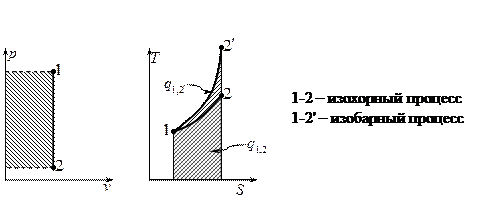
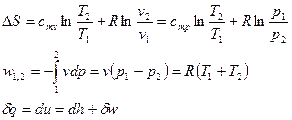
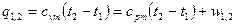
Вопрос №11.
Политропным процессом с постоянным показателем называется обратимый термодинамический процесс изменения состояния простого тела.
Уравнение политропного процесса с постоянным политропным показателем: 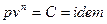 , (1)
, (1)
где 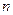 - политропный показатель, являющий в рассматриваемом процессе постоянной величиной, которая может иметь любые частные значения - положительные и отрицательные (-¥ £ n £ +¥). Физический смысл показателя политропы п определяется после дифференцирования выражения (1)
- политропный показатель, являющий в рассматриваемом процессе постоянной величиной, которая может иметь любые частные значения - положительные и отрицательные (-¥ £ n £ +¥). Физический смысл показателя политропы п определяется после дифференцирования выражения (1)
Тогда:
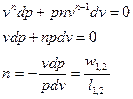
Это значит, что постоянный показатель политропы определяется соотношением потенциальной и термодинамической работ в элементарном или конечном процессах.
Показателем политропного процесса является линейная зависимость 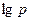 от
от  , то есть:
, то есть: 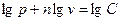 .
.

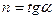
1. 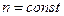
2. 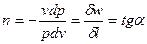 - истинный показатель политропы.
- истинный показатель политропы. 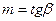 - второй средний показатель политропы.
- второй средний показатель политропы. 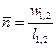 - первый средний показатель политропы.
- первый средний показатель политропы.
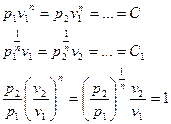
Если 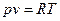 , то есть в случае идеального газа:
, то есть в случае идеального газа:
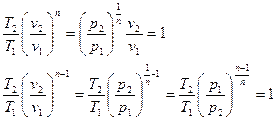
При этом политропный показатель может принимать значения в пределах от минус бесконечности до плюс бесконечности и оставаться постоянным в течение процесса. Если 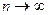 , то
, то 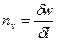 , следовательно
, следовательно 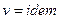 , то есть процесс изохорический. Если
, то есть процесс изохорический. Если 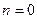 , то
, то 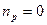 , следовательно
, следовательно 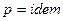 , то есть процесс изобарический. Если
, то есть процесс изобарический. Если 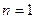 , то
, то 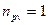 , следовательно
, следовательно 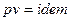 . Так как для идеального газа
. Так как для идеального газа 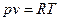 , то
, то 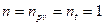 .
.
Если уравнением процесса является уравнение  , то в этом процессе
, то в этом процессе 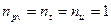 , следовательно
, следовательно 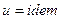 , то есть процесс изоэнергетический.
, то есть процесс изоэнергетический.
Для идеального газа 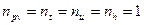 , следовательно
, следовательно 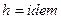 , то есть процесс изоэнтальпийный.
, то есть процесс изоэнтальпийный.
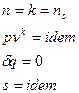
Работа: 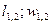 .
.
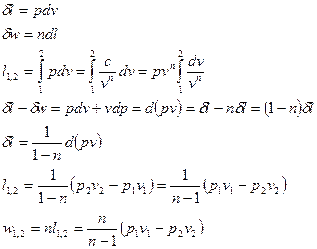
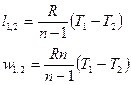 - для идеального газа.
- для идеального газа.
Характеристика растяжения (сжатия).
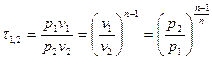
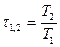 - для идеального газа.
- для идеального газа.
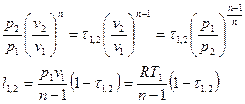
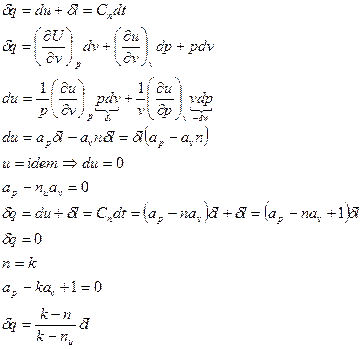
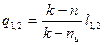 , где
, где 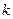 - показатель адиабаты,
- показатель адиабаты, 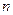 - политропный показатель,
- политропный показатель, 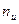 - показатель изоэнергетического процесса.
- показатель изоэнергетического процесса.
Для адиабатического процесса 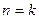 .
.
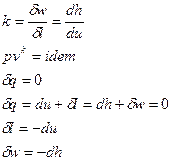
Все уравнения для политропного процесса остаются справедливы и для адиабатического процесса, только вместо политропного показателя используют адиабатический показатель.
Для идеального газа 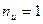 и
и 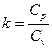
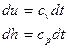
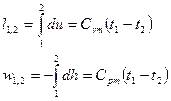
Вопрос №12.
Выражения конечных (интегральных) величин термодинамической и потенциальных работ в политропных процессах можно получить при сопоставлении их элементарных значений:
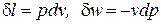 ; (1)
; (1)
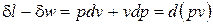 . (2)
. (2)
После подстановки выражения для показателя политропы 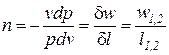 в соотношение (2) получаем
в соотношение (2) получаем
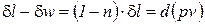 , (3)
, (3)
или
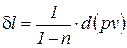 . (4)
. (4)
Интегрируя последнее выражение (4) с учетом того, что процесс подчиняется уравнению политропы с постоянным показателем (n=idem), получаем следующее соотношение для определения удельной термодинамической работы в конечном процессе (1-2)
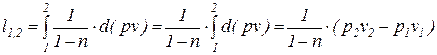 .
.
Вопрос №13
Теплообмен в любом термодинамическом процессе изменения состояния простых тел может быть выражен в зависимости от величины термодинамической или потенциальной работы процесса. При этом термодинамический процесс в общем случае рассматривается как политропа с переменным показателем.
Расчетное выражения теплообмена для простых тел выводится на основе рассмотрения выражения первого начала термодинамики
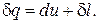 (1)
(1)
Удельная внутренняя энергия для простых тел может быть представлена в виде функции любых двух независимых параметров состояния. Примем, что u =и (p, v). Тогда дифференциал внутренней энергии запишется в следующем виде:
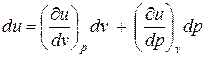 . (2)
. (2)
Последнее выражение (2) можно представить в виде
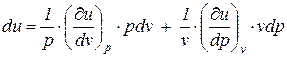 . (3)
. (3)
Введем следующие обозначения:
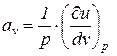 ;
; 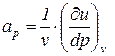 . (4)
. (4)
При этом выражение (3) примет вид:
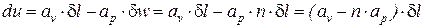 . (5)
. (5)
Сопоставляя соотношения (1) и (5), получим
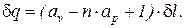 (6)
(6)
Для определения величин ( 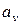 и
и 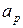 ) рассмотрим два термодинамических процесса:
) рассмотрим два термодинамических процесса:
1. Изоэнергетический процесс (u = idem, du = 0). Для этого процесса показатель политропы принимает значение n = nu.
Так как в изоэнергетическом процессе 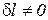 , из уравнения (5) следует, что
, из уравнения (5) следует, что
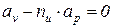 (7)
(7)
или
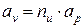 . (7а)
. (7а)
2. Адиабатный процесс(d q = 0). В этом процессе показатель политропы принимает значение n = k и называется показателем адиабаты.
В адиабатном процессе элементарная термодинамическая работа также не равна нулю, поэтому из выражения (6) имеем
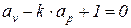 . (8)
. (8)
Сопоставляя соотношения (7) и (8), получаем следующие выражения:
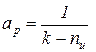 ,
, 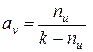 . (9)
. (9)
С учетом полученных соотношений для определения av и ap, находим выражения для расчета удельных значений изменения внутренней энергии и теплообмена в элементарном процессе:
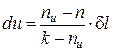 , (10)
, (10)
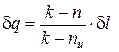 . (11)
. (11)
Соотношения для расчета удельных значений изменения внутренней энергии и теплообмена в конечном процессе имеют следующий вид:
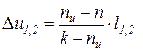 , (12)
, (12)
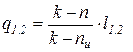 . (13)
. (13)
Вопрос №14
При изучении процессов изменения состояния идеальных газов, наряду с общими соотношениями по расчету термодинамических
процессов,следует использовать уравнение Клапейрона 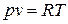
и закон Джоуля 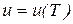
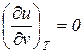 в соответствии с которыми для идеального газа справедливы следующие выражения:
в соответствии с которыми для идеального газа справедливы следующие выражения:
если 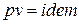 , то
, то 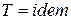 ; (1)
; (1)
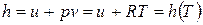 ; (2)
; (2)
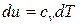 ; (3)
; (3)
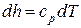 . (4)
. (4)
Из уравнений (1)¸(4) следует, что для идеального газа процессы изопотенциальный (pv =idem), изотермический (T = idem), изоэнергетический (u= idem) и изоэнтальпийный (h = idem) тождественны и, следовательно, показатели этих процеcсов равны
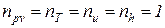 . (5)
. (5)
Характеристика расширения или сжатия процессов, в которых рабочим телом является идеальный газ, с учетом уравнения Клапейрона может быть определена по соотношению температур
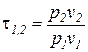 =
= 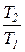 . (6)
. (6)
Изменения удельных значений внутренней энергии и энтальпии идеального газа в процессе в соответствии с законом Джоуля находится по следующим формулам:
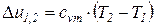 ; (7)
; (7)
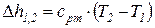 . (8)
. (8)
Показатель адиабатного процесса для идеального газа определяется как соотношение изобарной и изохорной теплоемкостей
k = ns = 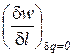 =
= 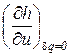 =
= 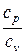 =
= 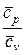 . (9)
. (9)
На основании закона Майера ( 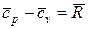 ) показатель адиабаты для идеального газа может быть определен из следующего соотношения:
) показатель адиабаты для идеального газа может быть определен из следующего соотношения:
k = 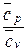 =
= 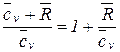 >1. (10)
>1. (10)
Для идеального газа показатель изоэнергетического процесса 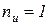 и поэтому удельное количество теплоты в элементарном процессе может быть определено по формуле
и поэтому удельное количество теплоты в элементарном процессе может быть определено по формуле
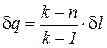 . (11)
. (11)
Вопрос №16.
Круговой процесс – процесс, который характеризуется возвратом в исходное состояние системы (рабочего тела).
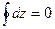
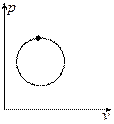 , где
, где 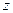 - любая из характеристик процесса, таких как давление, объём, температура, энергия, энтальпия и энтропия.
- любая из характеристик процесса, таких как давление, объём, температура, энергия, энтальпия и энтропия.
Циклы – периодически повторяющиеся в тепловых машинах круговые процессы.
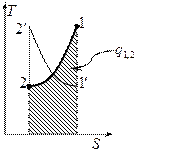
Если круговой процесс идёт по часовой стрелке это означает, что по верхней дуге тепло подводится, а по нижней отводится. Такой процесс называется прямым и реализуется в тепловых машинах.
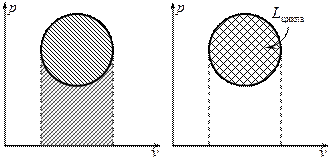 Если круговой процесс идёт против часовой стрелки это означает, что по нижней дуге идёт подвод тепла, а по верхней дуге идёт отвод тепла. Такой процесс называется обратным и реализуется в холодильных машинах.
Если круговой процесс идёт против часовой стрелки это означает, что по нижней дуге идёт подвод тепла, а по верхней дуге идёт отвод тепла. Такой процесс называется обратным и реализуется в холодильных машинах.
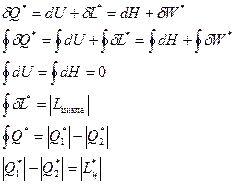
Различают три вида циклов тепловых машин: реальные, обратимые и термодинамические.
В реальных циклах тепловых машин имеют место внешняя и внутренняя необратимости.
Внешняя необратимость определяется конечной разностью температур между рабочим телом и источниками теплоты. Этим объясняется то, что реальный цикл теплового двигателя располагается внутри границ температур внешних источников, а реальный цикл холодильной машины - вне границ температур внешних источников .
Внутренняя необратимость обусловлена потерями энергии, связанными с трением, завихрениями и т.д. в процессах цикла.
В обратимых циклах тепловых машин отсутствует внешняя и внутренняя необратимости.
В термодинамических циклах тепловых машин, в отличие от реальных и обратимых циклов, рассматривается не вся система, включающая внешние источники теплоты, а только рабочее тело. При этом в процессах термодинамических циклов отсутствует внутренняя необратимость, то есть все процессы таких циклов являются обратимыми.
Эффективность любого реального теплового двигателя определяется коэффициентом полезного действия (КПД).
Коэффициент полезного действия реальных циклов тепловых двигателей численно равен отношению полученной работы к подведенному извне количеству теплоты
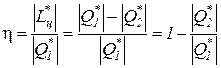 .
.
Для обратимого цикла теплового двигателя КПД определяется следующим образом:
h обр = 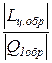 .
.
Термический коэффициент полезного действия термодинамического цикла теплового двигателя находится из соотношения
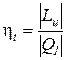 =
= 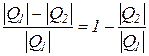 .
.
Эффективность циклов холодильных машин оценивается холодильным коэффициентом ( 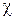 ). Холодильный коэффициент численно равен отношению количества теплоты, отводимой от холодного источника, к затраченной работе.
). Холодильный коэффициент численно равен отношению количества теплоты, отводимой от холодного источника, к затраченной работе.
Для реального цикла холодильной машины холодильный коэффициент определяется соотношением
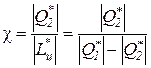 ,
,
для обратимого цикла холодильной машины – из зависимости
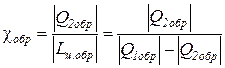 ,
,
а для термодинамического цикла холодильной машины – по соотношению
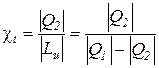 .
.
Вопрос №17
Цикл Карно.
1. Состоит из двух изотерм и двух адиабат.
2. Рабочее тело – идеальный газ.
3. Величины 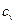 и
и 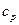 - постоянные.
- постоянные.
1-2, 3-4 – изотермические процессы.
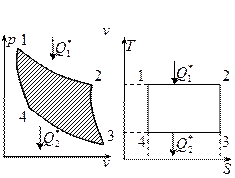 2-3, 4-1 -
2-3, 4-1 - 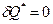 ,
, 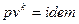 .
.
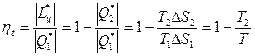 .
.
Подвод теплоты от горячего источника производится на изотерме 1-2 при температуре Т1, при этом рабочее тело - идеальный газ расширяется и совершается полезная работа. В процессе дальнейшего расширения по адиабате 2-3 до температуры Т2 также совершается полезная работа. Для осуществления последующих процессов - сжатия 3-4 по изотерме Т2 с отводом теплоты к холодному источнику и адиабатного сжатия 4-1 до начальной температуры Т1 работа затрачивается.
Термодинамический коэффициент полезного действия 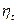 определяется температурами холодильника и нагревателя.
определяется температурами холодильника и нагревателя.
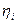 - индикаторный КПД.
- индикаторный КПД.
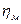 - механический КПД.
- механический КПД.
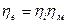 - эффективный КПД.
- эффективный КПД.
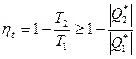
Вопрос №18
