Решение уравнений состояния в функции времени
Полное решение уравнения состояния (4.24) можно получить, применив теорему свёртки Лапласа к уравнению (4.28):
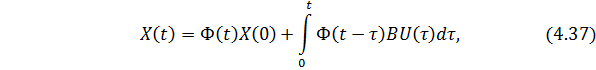
где 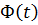 - матрица перехода в функции времени.
- матрица перехода в функции времени.
Трудность дальнейшего решения (4.37) связана с определением интеграла при произвольном векторе входа 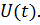 Однако в инженерной практике наибольший интерес представляют переходные характеристики, для получения которых следует положить
Однако в инженерной практике наибольший интерес представляют переходные характеристики, для получения которых следует положить 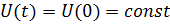 . В этом случае вычисление интеграла значительно упрощается.
. В этом случае вычисление интеграла значительно упрощается.
Определим сначала переходную матрицу Ф(t) в виде степенного ряда путём решения однородного уравнения состояния
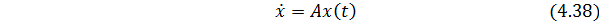
Положим
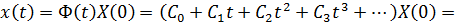
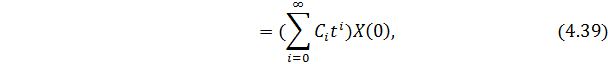
где 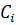 - квадратные матрицы, при этом
- квадратные матрицы, при этом 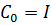 (очевидное значение, получаемое из (4.39) при t = 0).
(очевидное значение, получаемое из (4.39) при t = 0).
Подставив (4.39) в (4.38), получим соотношение
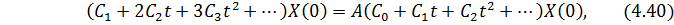
из которого при t = 0 имеем
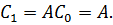
Далее после дифференцирования (4.40) получим следующее выражение
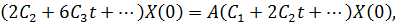
из которого при t = 0 определим, что
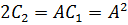
или
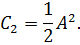
Используя подобную процедуру, получим в итоге рекуррентное соотношение, связывающее 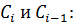
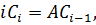
из которого общую формулу вычисления коэффициентов 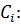
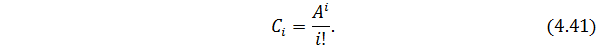
Таким образом, переходная матрица имеет вид экспоненциального матричного ряда:
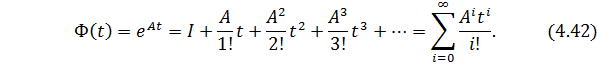
Это выражение часто называют матричным экспоненциалом. Такая форма Ф(t) позволяет выявить ряд полезных свойств матрицы перехода:
1) 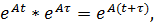 т.е.
т.е. 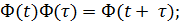
2) 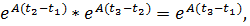 т.е.
т.е. 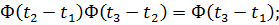
3) 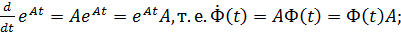
4) 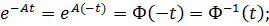
5) 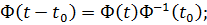
6) 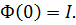
Здесь следует заметить, что вычисление матричного экспоненциала осуществляется приближённо. При этом точность расчёта в значительной мере определяется скоростью сходимости ряда (4.42). Не вдаваясь в эту проблему можно только рекомендовать использование для вычисления матрицы перехода в виде степенного ряда специальных математических пакетов, в частности MatLab.
В ряде случаев, обычно для динамических систем невысокого порядка, можно применять точные методы расчёта Ф(t). К ним относятся выше рассмотренные способы определения Ф(s) в виде передаточных функций.
Для получения матрицы Ф(t) на основе Ф(s) целесообразно использовать метод разложения передаточных функций 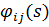 на сумму элементарных составляющих с последующим применением обратного преобразования Лапласа. Рассмотрим эту методику применительно к Ф(s), полученной в примере 4.6.
на сумму элементарных составляющих с последующим применением обратного преобразования Лапласа. Рассмотрим эту методику применительно к Ф(s), полученной в примере 4.6.
Пример 4.7. Вычислить матрицу перехода Ф(t) по её передаточной матрице Ф(s), определённой с помощью алгоритма Фаддеева-Леверье в примере 4.6:
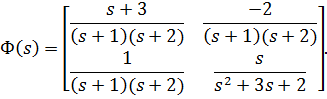
Сначала разложим передаточные функции 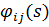 на элементарные составляющие с помощью вычетов:
на элементарные составляющие с помощью вычетов:
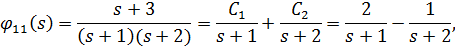
т.к. 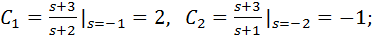
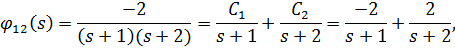
т.к. 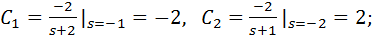
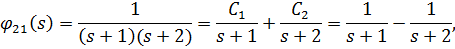
т.к. 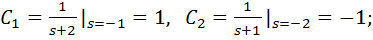
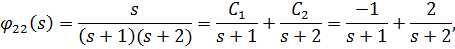
т.к. 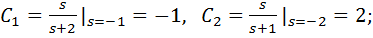
Далее, используя таблицу преобразования Лапласа, получим искомую Ф(t):
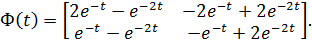
Теперь можно вернуться к определению переходной характеристики по уравнению (4.37), используя соответствующие свойства матричного экспоненциала. Будем искать решение при 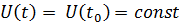 на интервале
на интервале 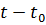 , где
, где 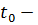 начальное время. В этом случае имеем
начальное время. В этом случае имеем
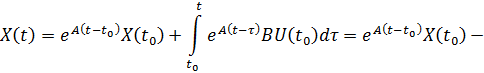
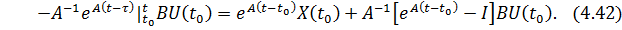
При расчёте переходных процессов удобнее пользоваться дискретным вариантом полученного решения. Для этого положим 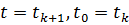 и
и 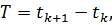 где T – шаг дискретизации вычислительного процесса. После ввода данного обозначения соотношение (4.42) можно записать в следующем виде:
где T – шаг дискретизации вычислительного процесса. После ввода данного обозначения соотношение (4.42) можно записать в следующем виде:
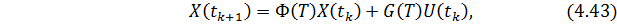
где 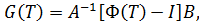
или в целом для стандартной формы уравнений состояния:
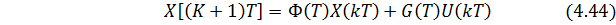
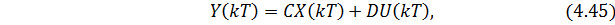
где k – номер шага дискретизации (k = 0, 1, 2…).
Следует заметить, что решение уравнения состояния в виде (4.43) позволяет определять переходные процессы в дискретных системах, в которых управляющее воздействие U(t) представляет собой последовательность прямоугольных импульсов. При этом интервал 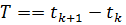 может изменяться от одного шага дискретизации к другому.
может изменяться от одного шага дискретизации к другому.
Следует заметить, что временные характеристики системы, описываемой уравнениями состояния, можно получить, воспользовавшись дискретной аппроксимацией этих уравнений с некоторым шагом T. Очевидно величина T ограничивается допустимой погрешностью вычислений. Разработанные в математике способы решения задачи аппроксимации образуют группу численных методов интегрирования дифференциальных уравнений, среди которых наибольшее применение в теории управления находят алгоритмы Эйлера и Рунге-Кутты.
Метод Эйлера основан на аппроксимации производной в виде разности первого порядка:
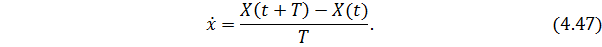
В результате уравнение состояния будет иметь следующий вид
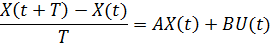
или
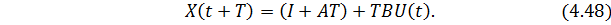
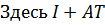 является переходной матрицей, которая по существу представляет первые два члена матричного ряда (4.42). Поэтому для достижения требуемой точности в методе Эйлера необходимо использовать очень малое значение T, что ведёт к значительному увеличению объёма вычислений и соответственно накоплению вычислительной погрешности.
является переходной матрицей, которая по существу представляет первые два члена матричного ряда (4.42). Поэтому для достижения требуемой точности в методе Эйлера необходимо использовать очень малое значение T, что ведёт к значительному увеличению объёма вычислений и соответственно накоплению вычислительной погрешности.
Более эффективными методами численного интегрирования являются алгоритмы Рунге-Кутты. Они используют аппроксимацию первых пяти членов ряда (4.42). Эти алгоритмы лежат в основе современных математических пакетов моделирования динамических систем, в частности, Simulink (приложение MatLab).
