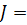Диагональная каноническая форма

Особое место в методе пространства состояний занимает диагональная каноническая форма (ДКФ). Она требует разложения передаточной функции динамической системы на элементарные составляющие. При этом следует выделить два случая: когда все полюсы различные и когда имеются кратные полюсы. Рассмотрим сначала вариант некратных корней знаменателя ПФ.

Пусть передаточная функция имеет следующий вид:

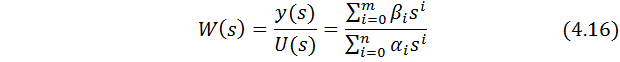
Её можно представить в виде суммы элементарных составляющих первого порядка:

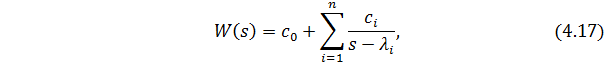
где 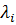- корни знаменателя (полюсы) ПФ.

Коэффициенты 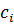определяются с помощью вычетов:

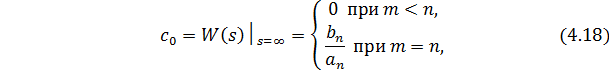
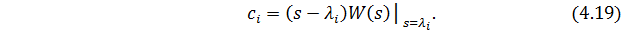
Для составляющей разложения (4.17) 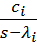можно построить элементарную РМ (рис. 4.14); используя метод интегрирования старшей производной:

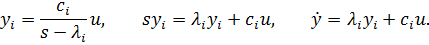
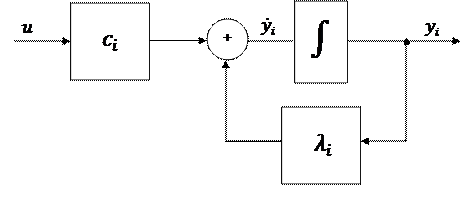Рис. 4.14

Коэффициент 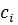можно переместить на выход этой модели, что обычно и делается. Используя элементарные РМ и разложение 4.17 можно построить искомую РМ, представленную на рис. 4.15.

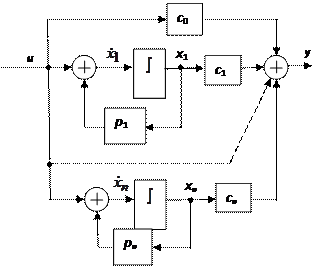Рис. 4.15

По данной РМ легко определить уравнения состояния:

………………………………………………

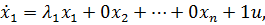
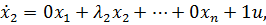
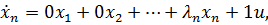
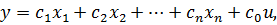
или в векторно-матричной форме

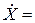ΛX+bu, (4.20)

y=c^TX+du, (4.21)

где

Λ 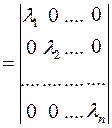; ; 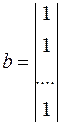; 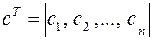d=c₀ .

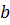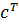Для получения ДКФ можно воспользоваться специальной функцией MatLab canon(w,’model’), где w – модель ПФ w(s), ‘model’ – модификатор диагональной формы, однако выражения для и отличаются от полученных в (4.20), (4.21) за счёт перераспределения коэффициентов при сохранении

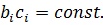
Пример 4.3. Определить ДКФ для динамической системы, заданной передаточной функцией

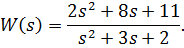
Полюсы в этой ПФ очевидно равны: 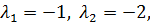поэтому можно записать

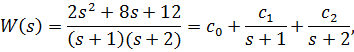
где

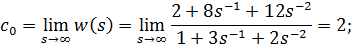
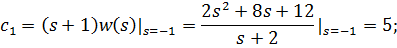
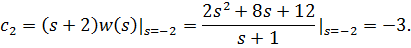
Отсюда

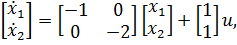
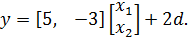
Передаточные функции САУ очень часто имеют комплексно-сопряжённые полюса, 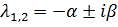которые определяют в итоге колебательность переходных характеристик системы. РМ колебательного звена с передаточной функцией

-

представлена на рис. 4.16.

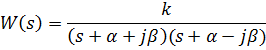
Рис. 4.16

Можно показать, что ПФ этой структуры равна

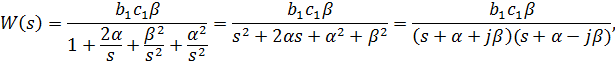
т.е. это ПФ колебательного звена, где 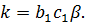При этом коэффициенты 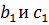можно объединить, но для согласованности с результатом функции canon(w,’modal’) целесообразно оставить указанный вид 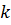без изменения.

По РМ колебательного звена можно определить уравнения состояния

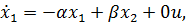
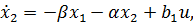
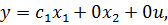
т.е. имеем

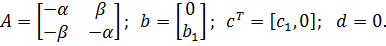
Следует обратить внимание на клеточную структуру матрицы 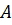, на диагонали которой расположены вещественные части полюсов ПФ w(s).

Пример 4.4. Используя функцию canon получить ss – модель в пространстве состояний для динамической системы с передаточной функцией

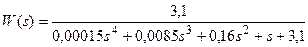
>> W=tf(3.1,[0.00015, 0.0085, 0.16, 1 ,3.1]);

>> sys=canon(W,'modal')

a =

x1 x2 x3 x4

x1 -24.41 7.474 0 0

x2 -7.474 -24.41 0 0

x3 0 0 -3.928 4.036

x4 0 0 -4.036 -3.928

b =

u1

x1 1.381

x2 16.39

x3 -1.761

x4 4.888

c =

x1 x2 x3 x4

y1 0.2856 0.193 2.02 0

d =

u1

y1 0

Continuous-time model.

Результаты решения показывают, что ПФ имеет две пары комплексно-сопряжённых корней: 24.41 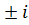7.474, 3.928 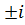4.036.

Иногда передаточная функция может содержать кратные полюсы. Это самый трудный вариант определения уравнений состояния в форме ДКФ.

Если имеется 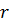кратных полюсов, то разложение на сумму простых дробей осуществляется с использованием вычетов в следующем виде

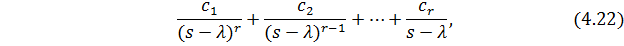
где

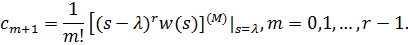
Пример 4.5. Получить уравнения состояния динамической системы по её ПФ

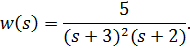
Очевидно ПФ имеет два кратных и один простой полюсы 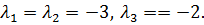Исходя из этого, разложение ПФ на сумму элементарных составляющих имеет следующий вид

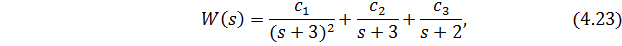
т.е. в (4.22) r=2 и соответственно

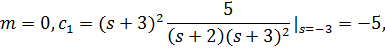
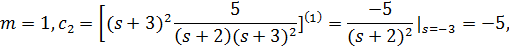
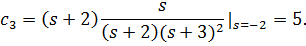
Разложение (4.23) позволяет построить РМ, представленную на рис. 4.17.

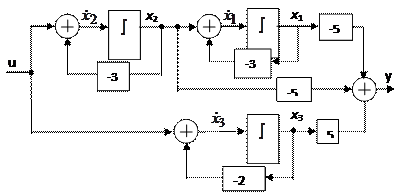Рис. 4.17

Данная РМ описывается следующей системой уравнений состояния:

т.е. для матриц уравнений состояния в форме ДКФ имеем:

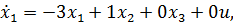
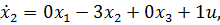
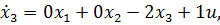
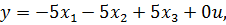
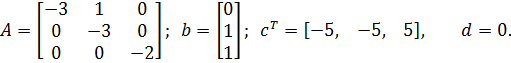
Следует отметить, что в матрице 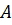появился специфический блок, выделенный пунктиром. Он называется клеткой Жордана, в связи с чем полученная форма уравнений состояния часто называется канонической формой Жордана с матрицей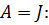

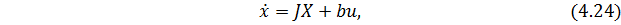
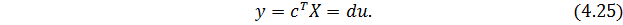
В общем случае для r кратных корней 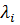фрагмент матрицы J имеет следующую структуру:

Т.е. клетка Жордана имеет единичную наддиагональ размером r-1.