Теоретическая механика занимается исследованием систем дискретных материальных точек, механика же сплошной среды рассматривает равновесие и движение газов, жидкостей и твердых тел, масса которых считается распределенной непрерывно. Вместе с массой непрерывно распределены по объему тела и силы, обусловленные наличием массы, например, сила тяжести. Кроме таких пространственно-распределенных сил в сплошной среде действуют также поверхностно распределенные силы.
В недеформированном теле все его части находятся в механическом равновесии. Это значит, что если выделить внутри тела какой-нибудь объем, то равнодействующая всех сил, действующих на этот объем со стороны других частей, равна нулю. При деформировании же тело выводится из состояния равновесия, в котором оно находилось первоначально. В нем возникают силы, стремящиеся вернуть тело в состояние равновесия. Эти возникающие при деформации внутренние силы называются внутренними напряжениями. Если тело не деформировано, то внутренние напряжения в нем отсутствуют. Внутренние напряжения обуславливаются силами взаимодействия молекул тела друг с другом. Молекулярные силы обладают очень незначительным радиусом действия. Их влияние простирается вокруг создающей их частицы лишь на расстояниях порядка межмолекулярных. Поэтому силы, обуславливающие внутренние напряжения, являются силами «близкодействующими», передающимися от каждой точки только к ближайшим с нею точкам. Отсюда следует, что силы, действующие на какую-то часть тела со стороны окружающих ее частей, действуют только непосредственно через поверхность этой части.
Проведем мысленно через точку 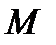 сплошной среды, например, упругого твердого тела, малую плоскую площадку величиной
сплошной среды, например, упругого твердого тела, малую плоскую площадку величиной 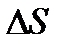 и восставим к одной из двух ее сторон нормальный единичный вектор
и восставим к одной из двух ее сторон нормальный единичный вектор 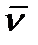 (рис 3).
(рис 3).
Часть тела, расположенную от площадки в направлении нормали 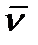 назовем внешней, а часть, расположенную по другую сторону площадки – внутренней. На внутреннюю часть со стороны внешней через площадку
назовем внешней, а часть, расположенную по другую сторону площадки – внутренней. На внутреннюю часть со стороны внешней через площадку 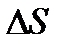 действует сила
действует сила 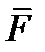 . Если эту силу
. Если эту силу 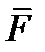 разделить на площадь
разделить на площадь 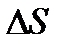 площадки, то получится среднее напряжение
площадки, то получится среднее напряжение 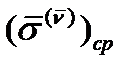 :
: 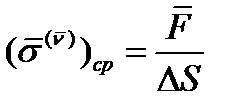 (9)
(9)
на площадке, проходящей через точку
с нормалью
. Переходя к пределу при стягивании площадки к точке
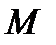
, получим истинное напряжение в точке
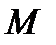
на элементарной площадке с номалью
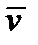
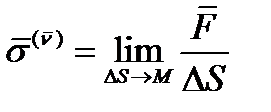
(10)
Меняя направление нормали
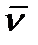
, т.е. поворачивая площадку, получим различные значения вектора напряженности
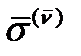
в одной и той же точке
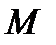
. Таким образом, напряженное состояние в точке
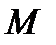
тела не может быть описано одним вектором. Но оказывается, что достаточно знать векторы напряжения на трех взаимно перпендикулярных площадках, проходящих через точку
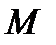
, и тогда можно найти напряжение в точке
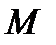
на площадке любой ориентации, проходящей через точку
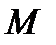
. Докажем это. Обозначим через
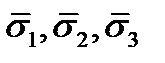
векторы напряжения в точке
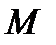
на элементарных площадках, нормали к которым совпадают по направлению с осями координат
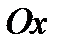
,
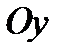
,
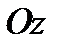
. Рассмотрим малый элементарный тетраэдр, три ребра которого параллельны осям координат (рис 4).
Пусть грань 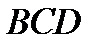 имеет площадь
имеет площадь 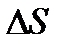 и внешнюю нормаль
и внешнюю нормаль 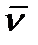 . Тогда площади граней
. Тогда площади граней 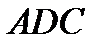 ,
, 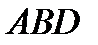 и
и 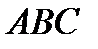 можно записать в виде:
можно записать в виде:
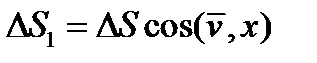 ,
, 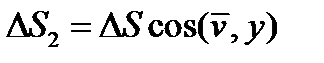 ,
, 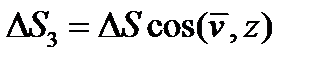 .
.
Внешние нормали к этим граням направлены по отрицательным направлениям координатных осей. Напряжение на площадке  , соответствующее внешней нормали
, соответствующее внешней нормали 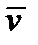 ,обозначим
,обозначим 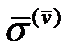 , а сила, действующая на этой площадке, будет равна
, а сила, действующая на этой площадке, будет равна 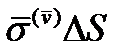 . Напряжение на площадке
. Напряжение на площадке 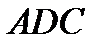 с нормалью, совпадающей по направлению с осью
с нормалью, совпадающей по направлению с осью 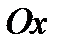 , обозначим
, обозначим 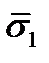 , тогда напряжение на той же грани, но с нормалью, противоположно направленной, по третьему закону Ньютона будет равно
, тогда напряжение на той же грани, но с нормалью, противоположно направленной, по третьему закону Ньютона будет равно 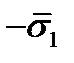 , а сила
, а сила 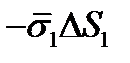 . Аналогично, сила на площадке
. Аналогично, сила на площадке 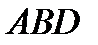 c нормалью, противоположной оси
c нормалью, противоположной оси 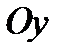 , будет равна
, будет равна 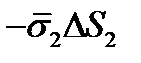 , а сила на площадке
, а сила на площадке  с нормалью, противоположной
с нормалью, противоположной  , будет равна
, будет равна 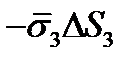 . Составим уравнение движения, пользуясь вторым законом Ньютона:
. Составим уравнение движения, пользуясь вторым законом Ньютона:
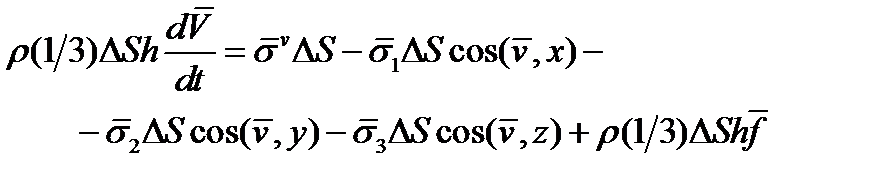 (11)
(11)
Здесь 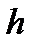 – высота тетраэдра, если за основание взять грань
– высота тетраэдра, если за основание взять грань  ,
, 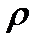 – плотность массы,
– плотность массы, 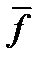 – объемная сила, приходящаяся на единицу массы (например, сила тяжести),
– объемная сила, приходящаяся на единицу массы (например, сила тяжести), 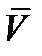 – скорость движения тетраэдра,
– скорость движения тетраэдра, 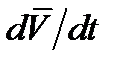 – ускорение;
– ускорение; 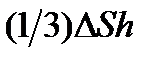 – объем тетраэдра. Разделим равенство (11) на
– объем тетраэдра. Разделим равенство (11) на 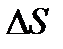 и перейдем к пределу, стягивая тетраэдр в точку (
и перейдем к пределу, стягивая тетраэдр в точку ( 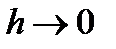 ). При этом учтем, что ускорение
). При этом учтем, что ускорение 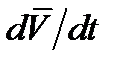 и объемная сила
и объемная сила 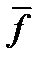 остаются ограниченными. В итоге получим равенство:
остаются ограниченными. В итоге получим равенство:
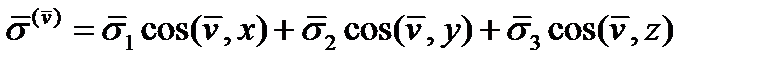 (12)
(12)
Так определяется вектор напряжения на площадке с произвольной ориентацией 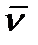 через напряжения
через напряжения 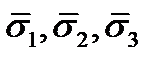 на площадках, нормали к которым совпадают по направлению с осями координат. Компоненты вектора
на площадках, нормали к которым совпадают по направлению с осями координат. Компоненты вектора 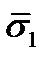 обозначим через
обозначим через 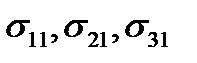 . Аналогично для векторов
. Аналогично для векторов 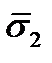 и
и 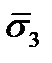 :
: 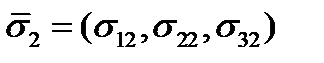 ,
, 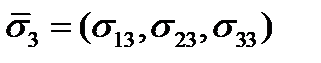 .
.
Расположим все эти компоненты в виде матрицы:
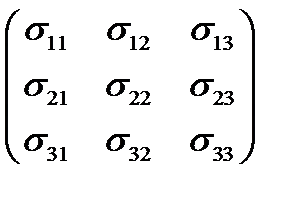 (13)
(13)
Таким образом, чтобы определить напряженное состояние в некоторой точке, нужно знать девять элементов матрицы (13). Элементы матрицы (13) имеют простой механический смысл. Так как вектор 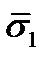 с компонентами
с компонентами 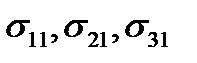 представляет собой напряжение, которое действует на малую площадку, перпендикулярную оси
представляет собой напряжение, которое действует на малую площадку, перпендикулярную оси 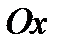 , то величина
, то величина 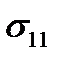 – это составляющая напряжения
– это составляющая напряжения 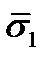 , перпендикулярная этой площадке. Эта составляющая называется нормальным напряжением на площадке. Составляющие
, перпендикулярная этой площадке. Эта составляющая называется нормальным напряжением на площадке. Составляющие 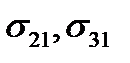 напряжения
напряжения 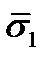 направлены по касательным к площадке и называются касательными напряжениями или напряжениями сдвига. Аналогично,
направлены по касательным к площадке и называются касательными напряжениями или напряжениями сдвига. Аналогично, 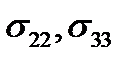 представляют собой нормальные напряжения на площадках, перпендикулярных осям
представляют собой нормальные напряжения на площадках, перпендикулярных осям 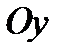 и
и 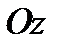 соответственно, а
соответственно, а 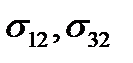 и
и 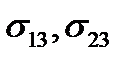 – напряжения сдвига. В теории упругости допускается, что матрица (13) симметрична, т.е.
– напряжения сдвига. В теории упругости допускается, что матрица (13) симметрична, т.е. 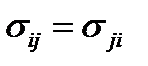 . В силу этого для определения напряженного состояния нужно знать не девять компонент напряжения, а только шесть. Так же, как и в первой задаче, матрица (13) обозначает тензор 2-ого ранга, называемый тензором напряжений. Компоненты тензора напряжений
. В силу этого для определения напряженного состояния нужно знать не девять компонент напряжения, а только шесть. Так же, как и в первой задаче, матрица (13) обозначает тензор 2-ого ранга, называемый тензором напряжений. Компоненты тензора напряжений 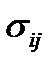 зависят от системы координат и изменяются при изменении системы координат по определенному правилу, которое будет установлено позднее.
зависят от системы координат и изменяются при изменении системы координат по определенному правилу, которое будет установлено позднее.
Таким образом, две задачи, совершенно разные по физическому содержанию, привели нас к одной и той же математической проблеме: необходимости изучения свойств и законов преобразования матриц вида (8) и (13), а также их обобщения. Аналогичная проблема возникает и в связи со многими другими задачами.
Теперь мы отвлекаемся от конкретного физического содержания и рассмотрим только математические аспекты. Прежде всего, заметим, что тензор 2-го ранга не тождественен квадратной матрице (3х3). Матрица – это лишь представление тензора в определенной системе координат, а сам тензор – инвариантный геометрический объект, существующий независимо от системы координат. Кроме того, матрицей вида (8) или (13) представляется лишь простейший тензор 2-го ранга. Тензоры более высокого ранга нельзя представить матрицей. Подробнее об этом будет сказано в следующих параграфах.
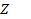
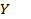
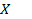
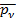
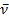
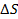
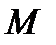 сплошной среды, например, упругого твердого тела, малую плоскую площадку величиной
сплошной среды, например, упругого твердого тела, малую плоскую площадку величиной 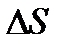 и восставим к одной из двух ее сторон нормальный единичный вектор
и восставим к одной из двух ее сторон нормальный единичный вектор 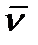 (рис 3).
(рис 3).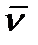 назовем внешней, а часть, расположенную по другую сторону площадки – внутренней. На внутреннюю часть со стороны внешней через площадку
назовем внешней, а часть, расположенную по другую сторону площадки – внутренней. На внутреннюю часть со стороны внешней через площадку 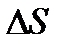 действует сила
действует сила 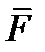 . Если эту силу
. Если эту силу 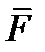 разделить на площадь
разделить на площадь 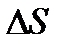 площадки, то получится среднее напряжение
площадки, то получится среднее напряжение 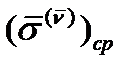 :
: 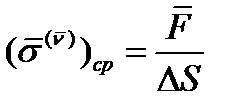 (9)
(9)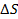
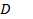
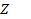
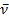
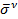
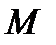 с нормалью
с нормалью 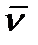 . Переходя к пределу при стягивании площадки к точке
. Переходя к пределу при стягивании площадки к точке 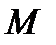 , получим истинное напряжение в точке
, получим истинное напряжение в точке 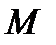 на элементарной площадке с номалью
на элементарной площадке с номалью 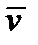
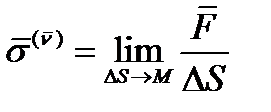 (10)
(10) 
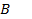
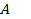
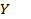
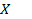
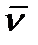 , т.е. поворачивая площадку, получим различные значения вектора напряженности
, т.е. поворачивая площадку, получим различные значения вектора напряженности 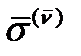 в одной и той же точке
в одной и той же точке 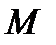 . Таким образом, напряженное состояние в точке
. Таким образом, напряженное состояние в точке 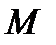 тела не может быть описано одним вектором. Но оказывается, что достаточно знать векторы напряжения на трех взаимно перпендикулярных площадках, проходящих через точку
тела не может быть описано одним вектором. Но оказывается, что достаточно знать векторы напряжения на трех взаимно перпендикулярных площадках, проходящих через точку 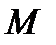 , и тогда можно найти напряжение в точке
, и тогда можно найти напряжение в точке 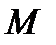 на площадке любой ориентации, проходящей через точку
на площадке любой ориентации, проходящей через точку 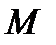 . Докажем это. Обозначим через
. Докажем это. Обозначим через 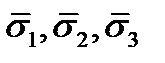 векторы напряжения в точке
векторы напряжения в точке 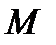 на элементарных площадках, нормали к которым совпадают по направлению с осями координат
на элементарных площадках, нормали к которым совпадают по направлению с осями координат 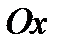 ,
, 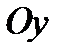 ,
, 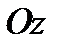 . Рассмотрим малый элементарный тетраэдр, три ребра которого параллельны осям координат (рис 4).
. Рассмотрим малый элементарный тетраэдр, три ребра которого параллельны осям координат (рис 4). 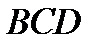 имеет площадь
имеет площадь 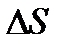 и внешнюю нормаль
и внешнюю нормаль 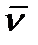 . Тогда площади граней
. Тогда площади граней 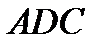 ,
, 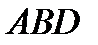 и
и 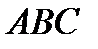 можно записать в виде:
можно записать в виде: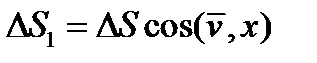 ,
, 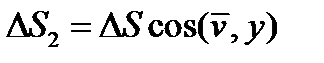 ,
, 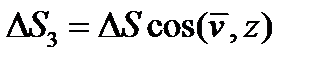 .
. , соответствующее внешней нормали
, соответствующее внешней нормали 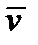 ,обозначим
,обозначим 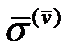 , а сила, действующая на этой площадке, будет равна
, а сила, действующая на этой площадке, будет равна 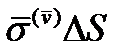 . Напряжение на площадке
. Напряжение на площадке 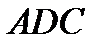 с нормалью, совпадающей по направлению с осью
с нормалью, совпадающей по направлению с осью 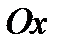 , обозначим
, обозначим 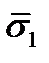 , тогда напряжение на той же грани, но с нормалью, противоположно направленной, по третьему закону Ньютона будет равно
, тогда напряжение на той же грани, но с нормалью, противоположно направленной, по третьему закону Ньютона будет равно 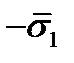 , а сила
, а сила 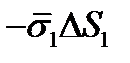 . Аналогично, сила на площадке
. Аналогично, сила на площадке 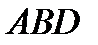 c нормалью, противоположной оси
c нормалью, противоположной оси  , будет равна
, будет равна 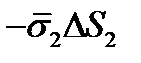 , а сила на площадке
, а сила на площадке  с нормалью, противоположной
с нормалью, противоположной  , будет равна
, будет равна 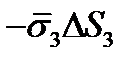 . Составим уравнение движения, пользуясь вторым законом Ньютона:
. Составим уравнение движения, пользуясь вторым законом Ньютона: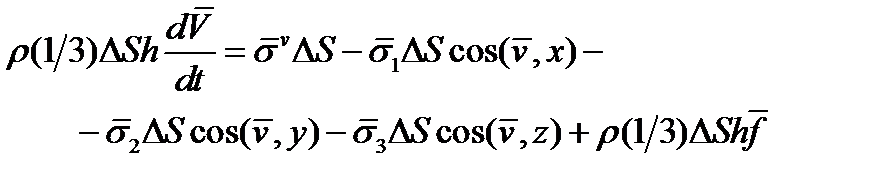 (11)
(11)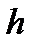 – высота тетраэдра, если за основание взять грань
– высота тетраэдра, если за основание взять грань 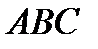 ,
, 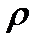 – плотность массы,
– плотность массы, 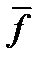 – объемная сила, приходящаяся на единицу массы (например, сила тяжести),
– объемная сила, приходящаяся на единицу массы (например, сила тяжести), 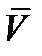 – скорость движения тетраэдра,
– скорость движения тетраэдра, 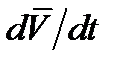 – ускорение;
– ускорение; 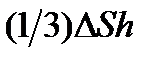 – объем тетраэдра. Разделим равенство (11) на
– объем тетраэдра. Разделим равенство (11) на 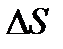 и перейдем к пределу, стягивая тетраэдр в точку (
и перейдем к пределу, стягивая тетраэдр в точку ( 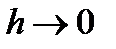 ). При этом учтем, что ускорение
). При этом учтем, что ускорение 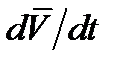 и объемная сила
и объемная сила 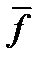 остаются ограниченными. В итоге получим равенство:
остаются ограниченными. В итоге получим равенство: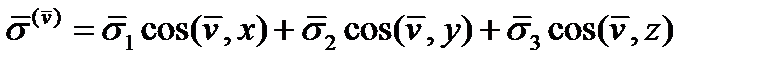 (12)
(12) через напряжения
через напряжения 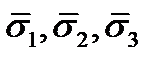 на площадках, нормали к которым совпадают по направлению с осями координат. Компоненты вектора
на площадках, нормали к которым совпадают по направлению с осями координат. Компоненты вектора 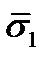 обозначим через
обозначим через 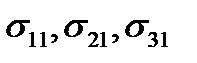 . Аналогично для векторов
. Аналогично для векторов 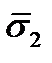 и
и 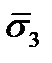 :
: 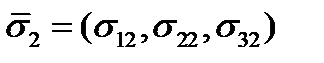 ,
, 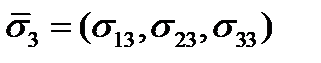 .
.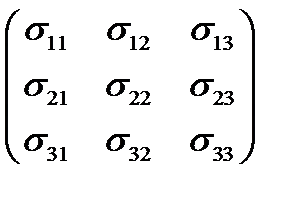 (13)
(13)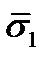 с компонентами
с компонентами 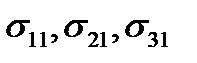 представляет собой напряжение, которое действует на малую площадку, перпендикулярную оси
представляет собой напряжение, которое действует на малую площадку, перпендикулярную оси 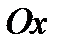 , то величина
, то величина 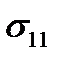 – это составляющая напряжения
– это составляющая напряжения 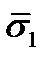 , перпендикулярная этой площадке. Эта составляющая называется нормальным напряжением на площадке. Составляющие
, перпендикулярная этой площадке. Эта составляющая называется нормальным напряжением на площадке. Составляющие 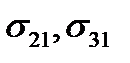 напряжения
напряжения 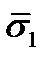 направлены по касательным к площадке и называются касательными напряжениями или напряжениями сдвига. Аналогично,
направлены по касательным к площадке и называются касательными напряжениями или напряжениями сдвига. Аналогично, 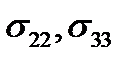 представляют собой нормальные напряжения на площадках, перпендикулярных осям
представляют собой нормальные напряжения на площадках, перпендикулярных осям 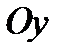 и
и 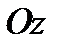 соответственно, а
соответственно, а 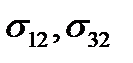 и
и 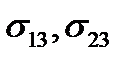 – напряжения сдвига. В теории упругости допускается, что матрица (13) симметрична, т.е.
– напряжения сдвига. В теории упругости допускается, что матрица (13) симметрична, т.е. 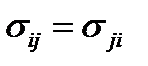 . В силу этого для определения напряженного состояния нужно знать не девять компонент напряжения, а только шесть. Так же, как и в первой задаче, матрица (13) обозначает тензор 2-ого ранга, называемый тензором напряжений. Компоненты тензора напряжений
. В силу этого для определения напряженного состояния нужно знать не девять компонент напряжения, а только шесть. Так же, как и в первой задаче, матрица (13) обозначает тензор 2-ого ранга, называемый тензором напряжений. Компоненты тензора напряжений 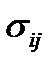 зависят от системы координат и изменяются при изменении системы координат по определенному правилу, которое будет установлено позднее.
зависят от системы координат и изменяются при изменении системы координат по определенному правилу, которое будет установлено позднее.