Симметричные и антисимметричные тензоры

Определение. Тензор 2-го ранга 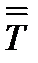называется симметричным, если он совпадает с транспонированным тензором 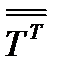. В координатах это запишется так:

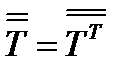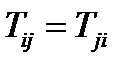, или (77)

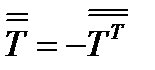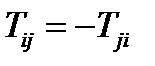Определение. Тензор 2-го ранга называется антисимметричным, если , или (78)

Докажем, что свойства симметричности и антисимметричности не зависят от системы координат. Для симметричного тензора это означает, что если в одной системе координат справедливо (77), то оно остается справедливым и в любой другой системе. Имеем при переходе к новой системе:

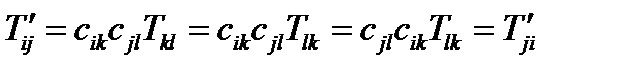(79)

Свойство антисимметричности (78) также инвариантно относительно преобразования системы координат:

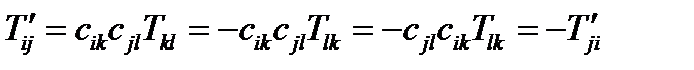(80)

Матрица симметричного тензора в любой системе координат симметрична, т.е. элементы ее, расположенные симметрично относительно главной диагонали, равны друг другу: .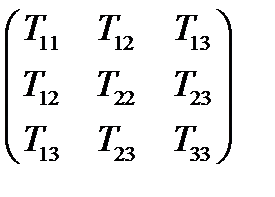

Матрица антисимметричного тензора в любой системе координат антисимметрична, т.е. элементы ее, расположенные симметрично относительно главной диагонали, равны по абсолютной величине, но противоположны по знаку. Элементы же, стоящие на главной диагонали, равны нулю, поскольку, например, 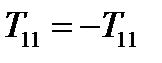, а это может быть только, если 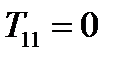. Аналогично и для остальных диагональных элементов. Матрица антисимметричного тензора, таким образом, имеет вид:

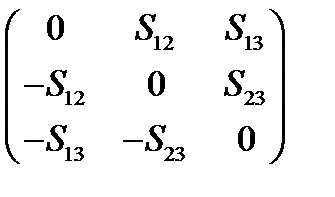
В силу всего сказанного симметричный тензор 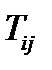определяется не девятью, а шестью компонентами 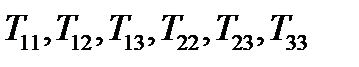, а антисимметричный тензор 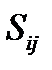– тремя компонентами .

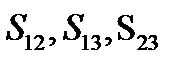Рассмотрим тождество:

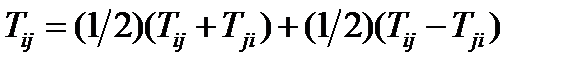(81)

Первый член в правой части является симметричным тензором, а второй – антисимметричным (докажите это самостоятельно). Следовательно, любой тензор 2-го ранга можно представить в виде суммы симметричного и антисимметричного тензоров. Это разложение единственно. В бескоординатной записи равенство (81) принимает вид: 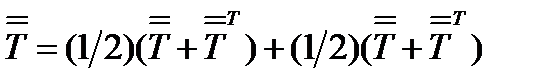(82)

Симметричная часть тензора обозначается через 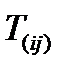, антисимметричная – через 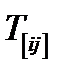, т.е.

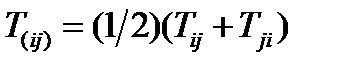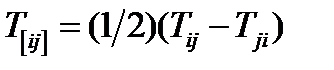, (83)

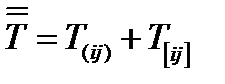и (84)

Задачи.

Задача 8. Как преобразуются компоненты тензора 2-го ранга, если система координат подвергается преобразованию, описанному в задаче 1 параграфа 8?

Решение. Исходим из формулы (70):

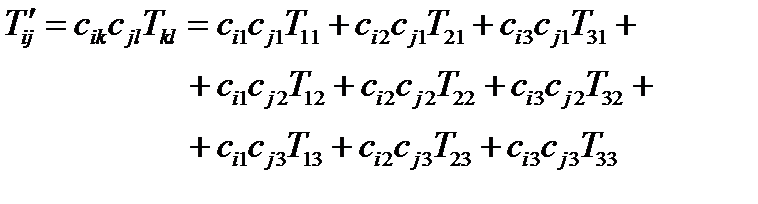(85)

Матрица преобразования системы координат определена в (52). Имеем:

, , ,

, ,

, ,

,

.

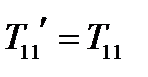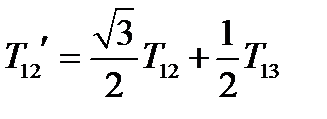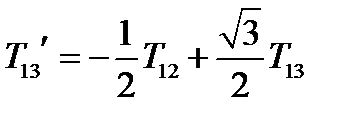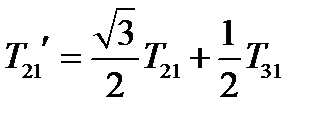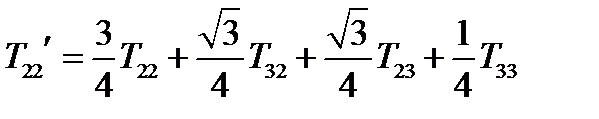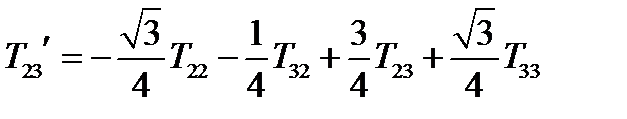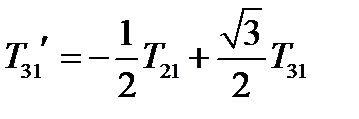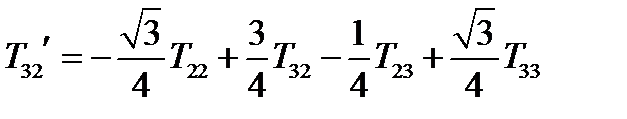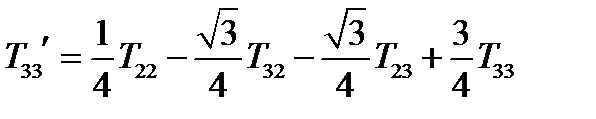На этом примере, в частности, легко убедиться, что свойство симметричности и антисимметричности присуще самому тензору и не зависит от системы координат.

Задача 9. Найти компоненты симметричного тензора в системе координат, получающейся с помощью преобразования, описанного в задаче 2 параграфа 8.

Решение. По формуле (85), используя матрицу преобразования (53) и симметричного тензора, получаем:

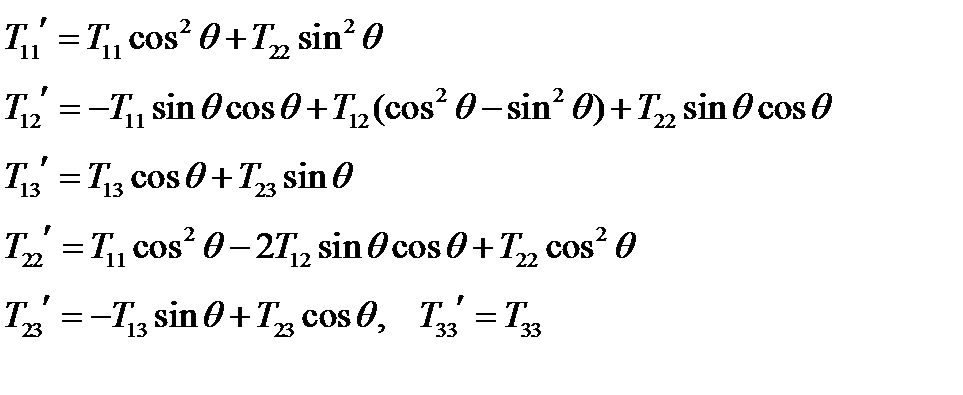(86)

В частности, если в старой системе координат матрица тензора была диагональной

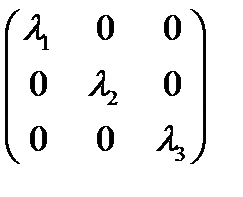, (87)

то в новой системе:

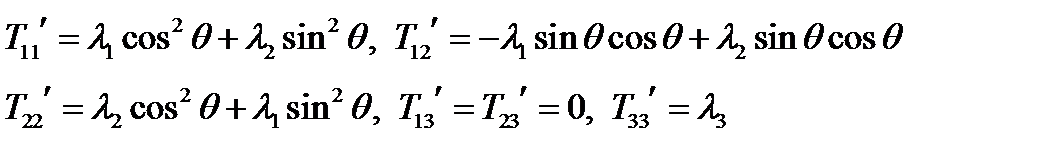(88)

Эти формулы обычно записывают в таком виде:

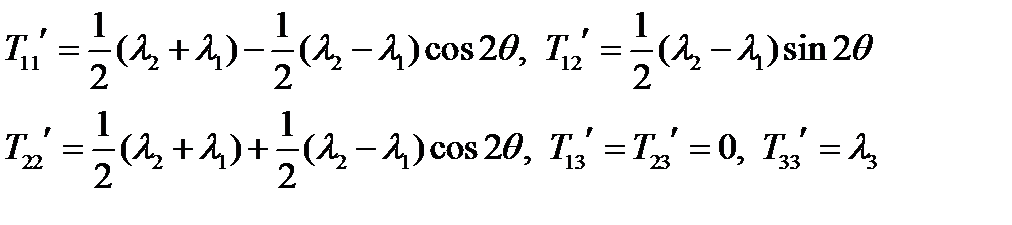(89)

Матрица тензора в новой системе координат будет иметь вид:

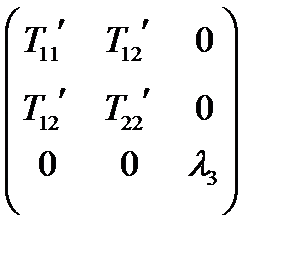(90)

Из (88)-(90) видно, что компонента тензора 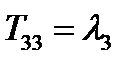при вращении системы координат вокруг оси 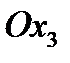остается неизменной. Формулы (89), (90) нам встретятся еще в дальнейшем.

Задача 10. Необходимо повернуть тензор: 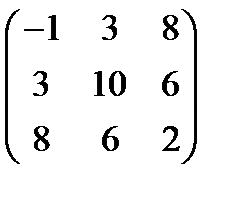вокруг оси 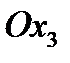так, чтобы компонента 22 стала равной нулю. Найти два возможных угла поворота, меньших 90 градусов.

Решение. Из (86) находим, что компонента 22 преобразуется по формуле: 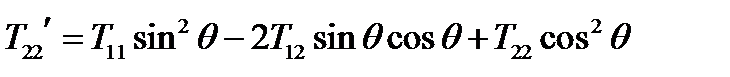. Поскольку 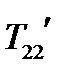должно быть равно нулю, то, подставляя 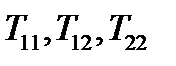, получаем уравнение: 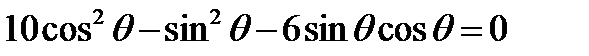или .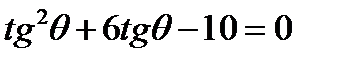

Решая его, получим: 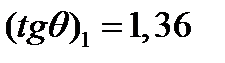, 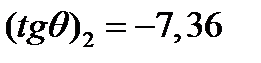. Отсюда 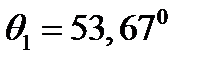, 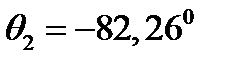. Следовательно, необходимый поворот системы координат можно осуществить двумя способами: повернуть вокруг оси 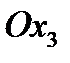в положительном направлении на угол 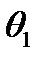(рис. 8а) или в отрицательном направлении на угол 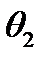(рисунок 8б).

Рис. 8б)

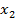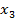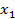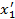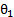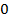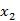Рис.8а) 8.8а)

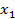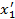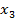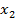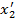Задача 11. Тензор электропроводности некоторого кристалла 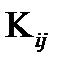имеет следующие компоненты в системе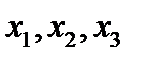 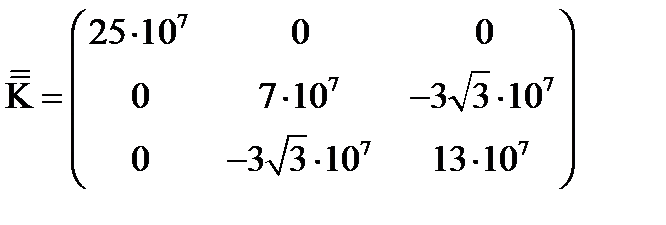(91)

Определить значение компонент тензора в системе координат, полученной с помощью преобразования, описанного в задаче 1 §8.

Решение. Исходим из формулы (85) и матрицы преобразования (52):

, , ,

, ,

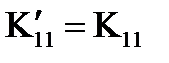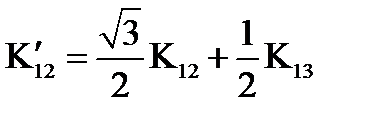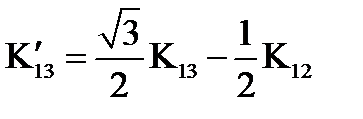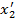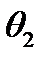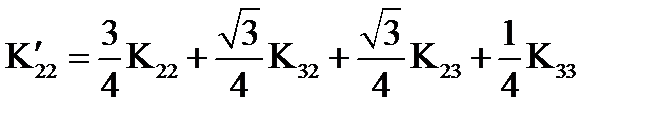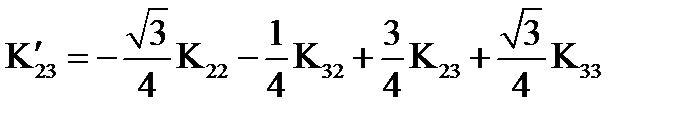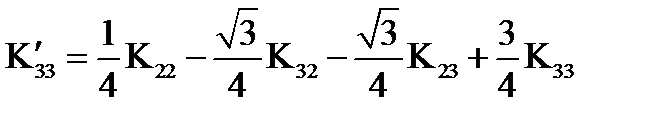
Подставляя значения «старых» компонент тензора 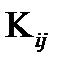из матрицы (91), получим в новой системе: .
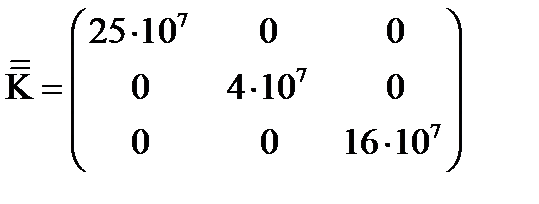В новой системе координат тензор электропроводности 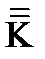стал диагональным. Забегая вперед, скажем, что оси координат, в которых матрица тензора приобретает диагональный вид, называются главными осями. Подробнее об этом будет говориться ниже.

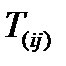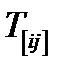Задача 12. Доказать, что тензоры и симметричен и антисимметричен соответственно.

Решение. Тензор 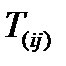– симметричная часть тензора 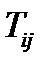определяется первой формулой в (83). Переставив в ней индексы 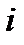и 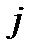, получим:

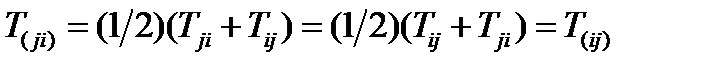(83)

Тензор 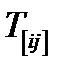– антисимметричная часть тензора 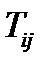– определяется второй формулой в (83). Переставляя в ней индексы 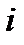и 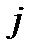, получим .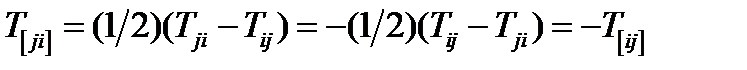