Решение симплексным методом

Решение задачи с дескриптивной моделью

Условие

При выполнении ремонтов локомотивов расходуются трудовые ресурсы, станко-часы и горюче-смазочные материалы (ГСМ). Месячный фонд рабочего времени ремонтных рабочих составляет 600 чел.-ч., фонд рабочего времени оборудования – 240 станко-часов, а месячный запас горюче-смазочных материалов составляет 200 т. Расходы ресурсов на выполнение одного ремонта определенного вида заданы в таблице. Требуется составить программу ремонтов.

Вид ресурсов	Расход ресурсов на выполнение 1 ремонта	Запасы (нормы расхода) ресурсов
	КР	ТР1	ТР2
Трудовые ресурсы	0,7	0,4	0,5
Станко-часы	0,3	0,2	0,4
ГСМ	0,5	0,3	0,3

Математическая модель

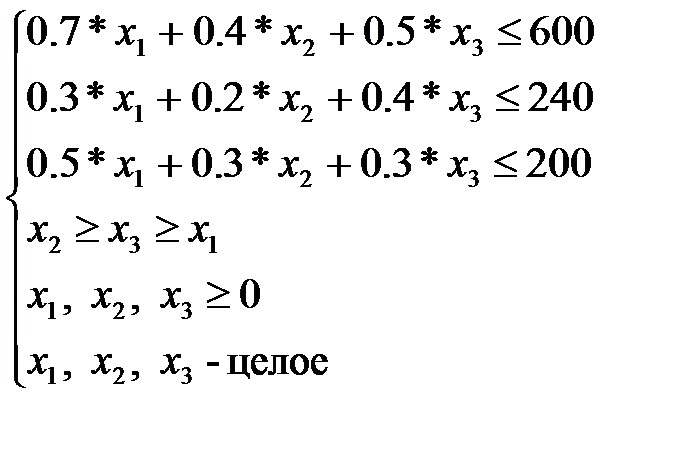
где: x₁ – кол-во капитальных ремонтов;

x₂ – кол-во 1-ых текущих ремонтов ;

x₃ – кол-во 2-ых текущих ремонтов.

Целевая функция f= x₁ + x₂ + x₃ –> mах количество выполненных ремонтов.

Результаты решения задачи с помощью MS Excel «Поиск решение»

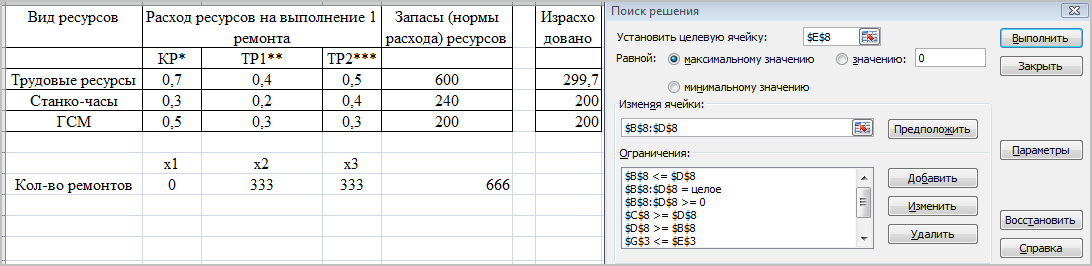
Вывод

Дескриптивные модели используются с целью количественного описания изучаемых процессов, т.е. с помощью модели находится один из вариантов возможного решения. Найденные значения переменных, и являются решением данной системы. Для нахождения оптимального решения требуется ввести целевую функцию и дополнительные ограничения.

Решение простейших оптимизационных моделей графоаналитическим методом

Условие

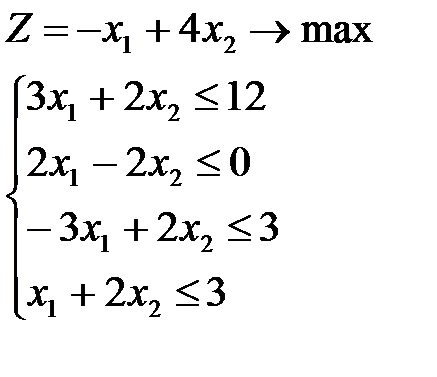
Решение графоаналитическим методом

Необходимо найти максимальное значение целевой функции F =-x₁-x₂ → max, при системе ограничений:

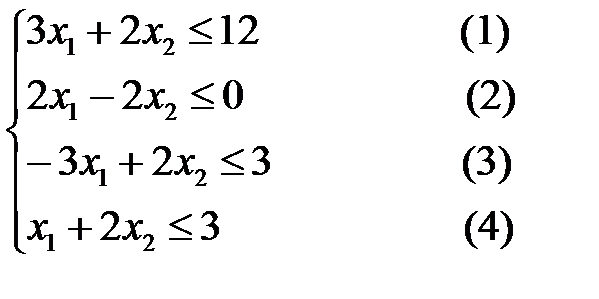
Чтобы найти область штриховки смотрим неравенства в условии задачи и подставляем ( 0; 0 ) для удобства вычислений.

Область решения, полученная графическим способом, представлена на рисунке

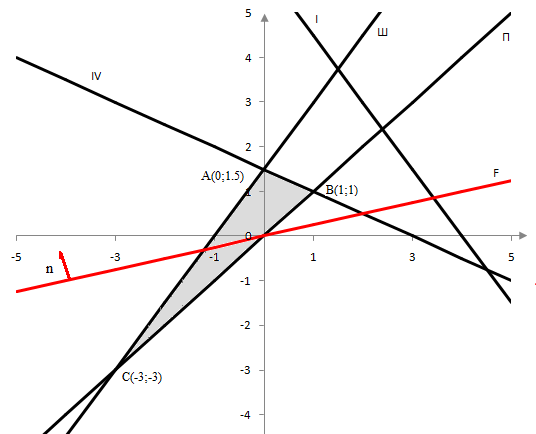
Для того чтобы получить максимальное значение целевой функции при заданных ограничениях, сдвигаем линию целевой функции в направление градиента. Перемещение продолжаем до тех пор, пока прямая F будет иметь хотя бы одну общую точку с многоугольником допустимых решений. Получим точку экстремума А(0;1,5). В этой точке функция будет принимать максимальное значение F(0;1,5)=6.

Для аналитического расчета координаты экстремальной точки, решим систему из двух уравнений, описывающих 3 и 4 линии, на пересечении которых находится точка экстремума.

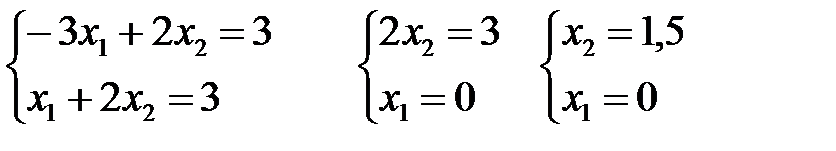
Получаем т.А(0;1,5)

Результаты решения модели с помощью «Поиск решение» MS Excel:

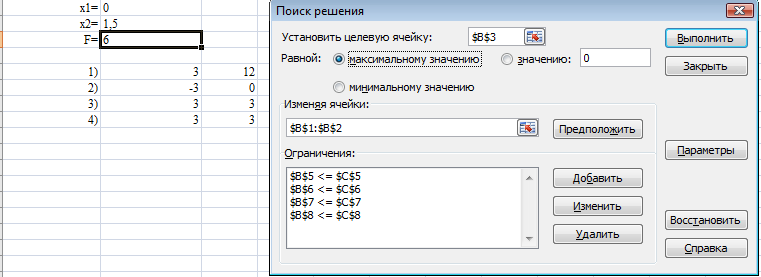
Вывод

С помощью графического построения системы ограничений модели определили на графике точку целевой функции, которая достигает своего экстремального значения, данное значение совпадает с решением компьютера.

Решение линейных математических моделей симплексным методом

Условие

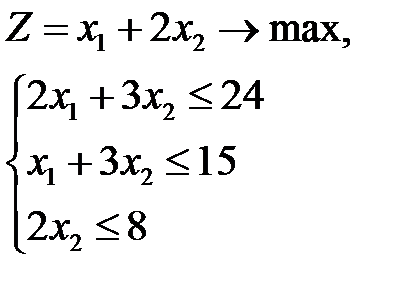
Решение симплексным методом

Для решения задачи введем дополнительные переменные ч3 ч4 ч5

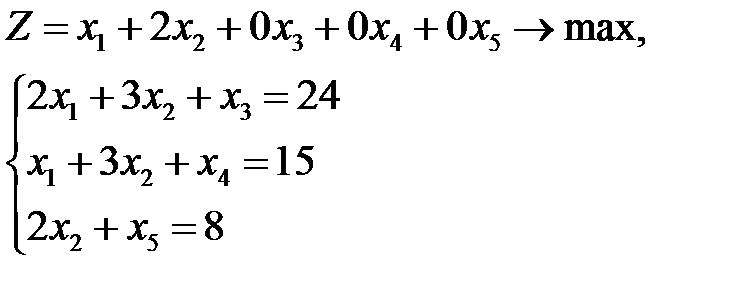
Таблица 3.1 – Исходная таблица

Сi	Базисные переменные	План
Х1	Х2	Х3	Х4	Х5	s
	Х3
	Х4
	Х5
Z(X)=		-1	-2

Таблица 3.2 – После 1 итерации

Сi	Базисные переменные	План
Х1	Х2	Х3	Х4	Х5	s
	Х3						-3
	Х4						-3
	Х2
Z(X)=		-1

Таблица 3.3 – После 2 итерации

Сi	Базисные переменные	План
Х1	Х2	Х3	Х4	Х5	s
	Х3					-2
	Х1						-3	-1
	Х2
Z(X)=						-1

Таблица 3.3 – После 3 итерации

Сi	Базисные переменные	План
Х1	Х2	Х3	Х4	Х5
	Х5				0,333	-0,667
	Х1					-1
	Х2				-0,333	0,667
Z(X)=				0,333	0,333

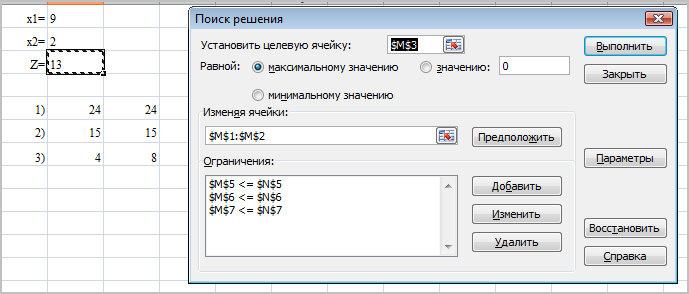
Z = 9 + 2×2 = 13

Результаты решения модели с помощью «Поиск решение» MS Excel:

Вывод.

При решении задачи симплексным методом получили оптимальное значение, которое соответствует отсутствию положительных значений в индексной строке и эти полученные значения совпадают с решением компьютера.