Модуль 3. Введение в математический анализ

Список вопросов к теоретической части экзамена по математике

гр. 1/30, 31, 32, 33

семестр 1 учебный год 2011/2012

Модуль 1. Высшая алгебра

УЭ 1.Матрицы. Основные определения. Действия над матрицами: линейные действия над матрицами, умножение матриц. Многочлены от матриц. Транспонирование матриц.

УЭ 2.Определители 2-го, 3-го и n порядка. Их свойства и вычисление.

УЭ 3.Обратная матрица. Ранг матрицы. Эквивалентные преобразования.

УЭ 4.Системы линейных уравнений. Решение систем линейных уравнений методом Крамера и методом Гаусса. Теорема Кронекера–Капелли.

Модуль 2. Аналитическая геометрия на плоскости и в пространстве. Элементы векторной алгебры

УЭ 5.Понятие вектора. Сложение векторов. Умножение вектора на скаляр. Критерий коллинеарности двух векторов.

УЭ 6.Понятие линейной зависимости (независимости) векторов. Понятие линейного (векторного) пространства. Базис в пространстве V₂ и теорема о разложение вектора по базису. Критерий компланарности трех векторов. Базис в пространстве V₃ и теорема о разложении вектора по базису. Переход от одного базиса к другому. Понятие ортонормированного базиса.

УЭ 7.Линейные операции над векторами в координатах. Скалярное произведение векторов. Свойства скалярного произведения. Выражение скалярного произведения через координаты сомножителей в ортонормированном базисе. Критерий ортогональности двух векторов. Длина вектора через координаты. Нахождение угла между векторами.

УЭ 8.Векторное произведение двух векторов. Свойства векторного произведения. Выражение векторного произведения через координаты сомножителей в правом ортонормированном базисе.

УЭ 9.Смешанное произведение трех векторов. Координатное выражение смешанного произведения в правом ортонормированном базисе. Критерий компланарности трех векторов через смешанное произведение.

УЭ 10.Системы координат. Аффинная система координат. Прямоугольная декартовая система координат. Полярная система координат. Цилиндрические и сферические координаты.

УЭ 11.Простейшие задачи аналитической геометрии на плоскости и в пространстве: нахождение координат прямой; задача о деление отрезка в заданном отношении; нахождение длины отрезка; нахождение площади треугольника, заданного координатами вершин; нахождение объема тетраэдра, заданного координатами вершин.

УЭ 12.Прямая на плоскости. Расположение прямой относительно осей координат. Взаимное расположение двух прямых. Пучок прямых. Простейшие задачи. Нормированное уравнение прямой. Расстояние от точки до прямой. Уравнение прямой в полярных координатах.

УЭ 13.Плоскость и ее уравнения. Расположение плоскости относительно координатных осей. Уравнение плоскости, заданной тремя точками, не принадлежащих одной прямой. Взаимное расположение двух плоскостей. Расстояние от точки до плоскости.

УЭ 14.Прямая в пространстве. Уравнение прямой, заданной двумя точками. Взаимное расположение двух прямых. Расстояние от точки до прямой. Расстояние между двумя прямыми. Взаимное расположение прямой и плоскости. Нахождение точек пересечения прямой и плоскости.

УЭ 15.Кривые второго порядка. Общее уравнение окружности. Эллипс. Гипербола. Директрисы эллипса и гиперболы. Парабола. Классификация кривых второго порядка.

УЭ 16.Цилиндрические поверхности. Уравнение цилиндрической поверхности с образующей, параллельной координатной оси. Цилиндры второго порядка. Конические поверхности. Поверхности вращения второго порядка. Эллипсоид. Гиперболоиды. Параболоиды.

Модуль 3. Введение в математический анализ

УЭ 17.Числовые множества. Отрезок, интервал, промежуток. Понятие функции. График функции. Функцияодной переменной. Сложная функция. Обратная функция. Основные элементарные функции, их графики.

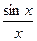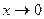УЭ 18.Предел функции. Бесконечно малые функции и их свойства. Бесконечно большие функции. Основные теоремы о пределах функции. Предел функции при . Число e. Натуральный логарифм. Раскрытие неопределенностей вида 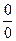и .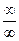

УЭ 19.Непрерывность функции в точке. Точки разрыва функции. Их классификация. Непрерывность функции на промежутке. Действия над непрерывными функциями. Непрерывность элементарных функций.