Численное интегрирование

Краткое введение Задача приближенного вычисления определенного интеграла (на отрезке или по многомерной области) фактически разбивается на две самостоятельные подзадачи. Первая — это интегрирование таблично заданной функции (полученной, например, при проведении лабораторного эксперимента). В таком случае информация о гладкости подынтегральной функции отсутствует, весьма ограничены возможности в выборе узлов интегрирования. Для этой задачи наиболее эффективными будут квадратурные формулы интерполяционного типа и правило Рунге оценки погрешности.

Вторая задача — подсчет значения определенного интеграла от известной функции. При этом самая ресурсоемкая операция с точки зрения вычислений — подсчет значения функции. Желательно построить численный метод, позволяющий получать как можно более высокую точность при наименьшем количестве вычислений. При этом выбор узлов квадратурных формул целиком определяется исследователем. В этом случае наиболее эффективными окажутся квадратурные формулы типа Гаусса.

Квадратурные формулы интерполяционного типа (формулы Ньютона - Котеса)

Геометрический смысл определенного интеграла функции f(x) заключается в площади фигуры, образованной этой функцией и осью OX. Поэтому самый простой способ посчитать определенный интеграл от "хорошей" (т.е. гладкой) функции - применить формулу прямоугольников или трапеций. C помощью этих формул площадь упомянутой искомой фигуры подсчитывается как сумма элементарных прямоугольников (или трапеций), множеством которых заменяется подынтегральная функция f(x).

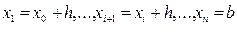Для подсчета интеграла интервал интегрирования [a,b] разбивается на n равных частей (отрезков) точками (h – шаг разбиения 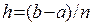. При этом точка x_i может выбираться, к примеру, как начало каждого элементарного отрезка, либо как его центр. Значение функции f(x) в точках разбиения х_i обозначим через у_i . Непрерывная подынтегральная функция заменяется сплайном – кусочно-полиномиальной функцией S(x), аппроксимирующей данную функцию. Очевидно, что при стремлении h к 0, множество прямоугольников (или трапеций) стремится к искомой фигуре, образованной подынтегральной функцией, а численный результат - к истинному значению интеграла.

Интегрируя функцию S(x) на отрезке [a,b], будем получать в зависимости от S(x) следующие квадратурные формулы:

Формула прямоугольников

Если на каждой части [x_i-1,…,x_i] (i=1,2,…,n) деления отрезка [a,b] функцию f(x) заменить функцией, принимающей постоянное значение, равное, например, значению функции f(x) в серединной точке i-й части , т.е на каждой части отрезка функция имеет вид прямоугольника с шириной и высотой f(x_i), то функция S(x) будет иметь ступенчатый вид:

, х Є [x_i-1,…,x_i], (i=1,2,…,n).

Отсюда получаем квадратурную формулу прямоугольников:

(1)

Конечно, для константы приведенная выше формула точна — говорят, что построенная квадратурная формула будет точна на полиномах степени 0. Легко можно доказать, что формула прямоугольников с центральной точкой будет давать точное значение и в случае линейной функции. Для всех других функций эту формулу будем рассматривать как приближенную.

Иллюстрация метода приведена на рис. 5.1

Рис. 5.1 Иллюстрация метода прямоугольников

Формула трапеций

Если предположить, что функция f(х) на отрезке интегрирования [a, b] достаточно близка к линейной, то данную функцию можно заменить на каждом отрезке [x_i-1,…,x_i] ее линейной интерполяцией по точкам (x_i-1 , у_i-1) и (x_i , у_i), т. е. ломаной линией с вершинами в концах элементарных отрезков, на которые разбивается интервал интегрирования( аппроксимация искомого интеграла множеством элементарных трапеций с высотой (b - a) и основаниями f(a) и f(b)).

. В результате получим кусочно-линейную функцию

, х Є [x_i-1,…,x_i], (i=1,2,…,n).

Здесь у_i=f(x_i).

Тогда формула трапеций будет иметь вид:

, (i=1,2,…,n) (2)

Иллюстрация метода приведена на рис. 5.2

Рис. 5.2 Иллюстрация метода трапеций

Формула Симпсона

- это формула парабол, которую можно получить при условии, что сплайн S(x), аппроксимирующий подынтегральную функцию f(x), представляет собой непрерывную функцию, составленную из примыкающих парабол. Пусть парабола на отрезке [x_i-1,…,x_i] проходит через точки (x_i-1 , у_i-1) , (x_i-1/2 , у_i-1/2) и (x_i , у_i). Используя построение интерполяционного многочлена Лагранжа второго порядка на данном отрезке получим сплайн:

х Є [x_i-1,…,x_i], (i=1,2,…,n).

Для дальнейших преобразований введем переменную t Є [0;1] с помощью равенства х = x_i-1 +ht . Значениям t, равным 0, ½, 1 соответствуют значения х, равные x_i-1 , x_{i-1/2 ,} x_i . Выразим сплайн S(x) через новую переменную:

(i=1,2,…,n).

Учитывая, что имеем

И в результате приходим к квадратурной формуле парабол:

(3)

Приближенное значение интеграла, вычисленного по квадратурным формуле парабол, можно выразить через результаты вычислений по квадратурным формулам прямоугольников и трапеций:

Иллюстрация метода приведена на рис. 5.3

Рис. 5.3 Иллюстрация метода Симпсона