Тема 4. Схема независимых испытаний Бернулли. Формула Бернулли. Наивероятнейшее число наступлений события

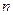На практике часто приходится сталкиваться с задачами, которые можно представить в виде многократно повторяющихся испытаний при данном комплексе условий, в которых представляет интерес вероятность числа к наступлений некоторого события в испытаниях. Например, необходимо определить вероятность определенного числа попаданий в мишень при нескольких выстрелах, вероятность некоторого числа бракованных изделий в данной партии и т.д.

Если вероятность наступления события в каждом испытании не меняется от исходов других, то такие испытания называются независимыми относительно события . Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события в каждом испытании одна и та же. Описанная последовательность независимых испытаний получила название схемы независимых испытаний Бернулли.

Теорема. Пусть производится 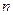независимых испытаний, в каждом из которых некоторое событие может появиться с вероятностью 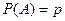и не появиться с вероятностью 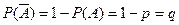. Тогда вероятность появления события 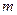раз в 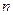испытаниях вычисляется по формуле Бернулли

,

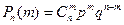где , .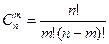

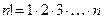Можно также посчитать вероятность того, что событие произойдет в 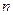испытаниях не более 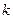раз ( 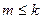) и более 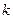раз ( ):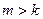

,

.

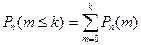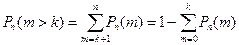Пример 1. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при шести выстрелах цель будет поражена четыре раза.

Решение. Искомую вероятность находим по формуле Бернулли. По условию задачи 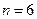, , 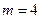, 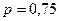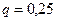. Тогда .

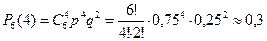Пример 2. Пусть в семье пятеро детей. С какой вероятностью в семье две девочки и трое мальчиков?

Решение. Пусть событию – «родилась девочка» соответствует вероятность 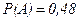Р(А), а событию 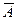«родился мальчик» – вероятность 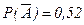. По условию задачи обозначениям, используемым в формуле Бернулли, соответствуют , , , .

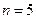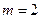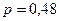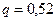В семье должны быть две девочки. Они не обязательно появляются одна за другой, возможны различные варианты, например,

( ), ( ), ( ) (*)

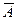
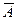
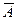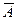
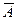
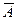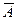
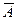
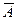и другие. Каково число семей, удовлетворяющих условию задачи?

При обозначении подходящих семей выбираем две позиции из пяти – число таких семей равно 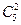. Имеем 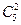сложных событий вида (*). Найдем вероятность каждого из них:

,

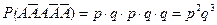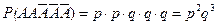и т.д.

Сложные события вида (*) попарно несовместны. Мы хотим, чтобы наступило хотя бы одно из них, т.е. нужно найти вероятность суммы несовместных событий. Вероятность каждого события равна p²q³, их число 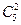, значит, искомая вероятность равна

.

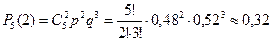Пример 3. В группе 10 студентов. Вероятность присутствия на занятиях отдельного студента равна 0,9. Какова вероятность того, что на занятиях будет присутствовать более 7 человек?

Решение. Обозначим - присутствие студента на занятиях.

По условию 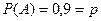. Тогда .

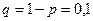Производится 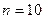опытов. Необходимо найти .

.

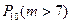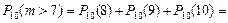
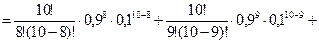
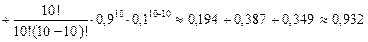Число 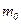называется наивероятнейшим числом наступления события в 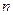испытаниях, если значение вероятности 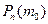не меньше остальных значений .

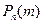Есл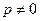и и 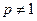, то число 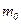можно определить из двойного неравенства

.

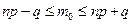Разность граничных значений в этом двойном неравенстве равна 1. Если 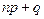не является целым числом, то двойное неравенство определяет лишь одно наивероятнейшее значение 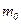. Если же 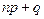- целое число, то имеются два наивероятнейших значения: 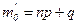и .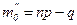

Пример 4. Вероятность попадания стрелком в цель равна 0,7. сделано 25 выстрелов. Определить наивероятнейшее число попаданий в цель.

Решение. Здесь 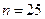, , 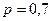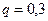. Следовательно,

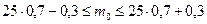, т.е. .

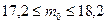Так как 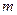- целое число, то .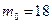