Тема 7. Числовые характеристики случайных величин

Закон распределения полностью характеризует случайную величину. Однако часто пользуются числовыми характеристиками случайной величины, которые дают некоторое осредненное описание случайной величины, получаемое на базе закона ее распределения.

1. Математическое ожидание.

Математическим ожиданием непрерывной случайной величины называется число

,

где 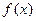- плотность вероятности случайной величины.

Математическим ожиданием дискретной случайной величины называется число

,

где 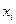- значение случайной величины,

- вероятность принять это значение.

Свойства математического ожидания:

1. , где - неслучайная величина.

2. .

3. .

4. Если и - независимые случайные величины, то .

5. Если все значения случайной величины уменьшить (увеличить) на одно и то же число , то ее математическое ожидание 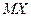уменьшится (увеличится) на то же число:

М.

Следствие. Математическое ожидание отклонения значений случайной величины от ее математического ожидания равно нулю: .

2. Дисперсия.

Дисперсией случайной величины называется

.

Используя свойства математического ожидания, дисперсию можно представить в виде

.

Свойства дисперсии:

1. .

2. , где - неслучайная величина.

3. .

4. Если и - независимые случайные величины, то .

3. Среднее квадратическое отклонение.

Третьей числовой характеристикой случайной величины является среднее квадратическое отклонение (стандартное отклонение или стандарт), обозначается оно 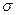и по определению оно равно квадратному корню из дисперсии:

Размерность дисперсии есть квадрат размерности самой случайной величины, а среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.

4. Моменты случайных величин.

Начальным моментом 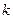-го порядка случайной величины называется

.

При начальный момент совпадает с математическим ожиданием

.

Центральным моментом 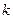-го порядка случайной величины называется

.

При центральный момент совпадает с дисперсией случайной величины

.

Помимо начального и центрального моментов определяются смешанные моменты, характеризующие две случайные величины и в совокупности.

Начальным смешанным моментом 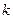-го порядка называется

, где .

Центральным смешанным моментом 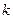-го порядка называется

, где .

Наиболее часто используется центральный смешанный момент 2-го порядка, который называется корреляционным моментом

.

Помимо корреляционного момента рассматривается нормированный корреляционный момент, который называется коэффициентом корреляции

Коэффициент корреляции характеризует степень связи между случайными величинами и .

Если случайные величины независимы, то коэффициент корреляции равен 0.

Для любых случайных величин . В случае, когда и связаны линейной зависимостью, .

Пример 1. Найти математическое ожидание случайной величины, заданной рядом распределения:

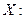0,1	0,4	0,3	0,2

Решение. .

Пример 2. Ежедневные расходы на обслуживание и рекламу автомобилей в автосалоне составляют в среднем 100 тыс.руб., а число продаж автомашин в течение дня подчиняется закону распределения:

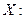0,25	0,2	0,1	0,1	0,1	0,1	0,05	0,05	0,025	0,025

Найти математическое ожидание ежедневной прибыли при цене на машину 150 тыс. руб.

Решение. Ежедневная прибыль вычисляется по формуле

тыс.руб.

(эту величину находим по определению математического ожидания).

Используя свойства математического ожидания, получаем

.

Пример 3. В лотерее разыгрывается 1000 билетов, из них выигрышных: 10 по 500 руб., 50 по 50 руб., 100 по 10 руб., 150 по 1 руб. Найти математическое ожидание выигрыша на один билет.

Решение. Случайная величина – сумма выигрыша на один билет. Значения случайной величины: 500, 50, 10, 1, 0.

, , , , .

Ряд распределения имеет вид:

0,01	0,05	0,1	0,15	0,69

руб.

Пример 4. В задаче с лотереей найти дисперсию выигрыша.

Решение.

.

Или .

Пример 5. Заданы законы распределения двух независимых случайных величин и :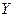

	-4
0,2	0,1	0,3	0,4

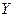0,2	0,8

Найти математическое ожидание и дисперсию случайной величины .

Решение. Найдем математические ожидания случайных величин и :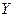

, .

Соответствующие дисперсии равны

Пользуясь свойствами математического ожидания, а также независимостью случайных величин и 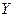, получим:

,

.