Задание 2. Вычисление значения функции
Вычислить значение функции в зависимости от условия.
Задание выполнить с помощью математического редактора MathCAD и процессора электронных таблиц Excel.
Варианты заданий представлены в табл. 2.
Таблица 2
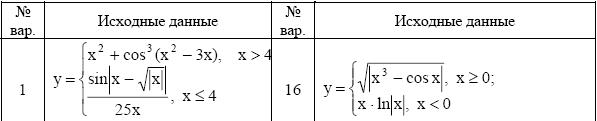


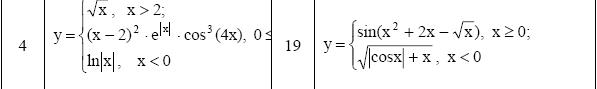
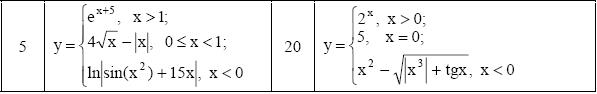
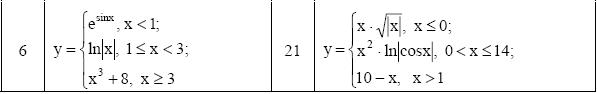
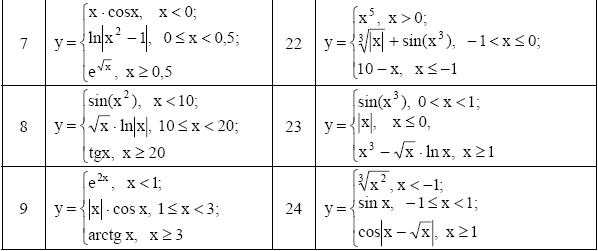

ЗАДАНИЕ 3. РЕШЕНИЕ УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
Определить решения уравнения f(x)=0 с точностью ε=10-4. Выбор начального приближения подтвердить графиком.
Задание выполнить с помощью математического пакета MathCAD (использовать встроенную функцию root) и процессора электронных таблиц MS Excel (использовать инструмент Подборпараметра).
Варианты заданий представлены в табл.3.
Таблица 3
| № вар | Исходные данные | № вар | Исходные данные | № вар | Исходные данные |
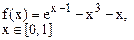 | 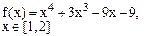 | 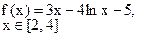 | |||
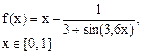 | 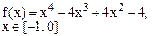 | 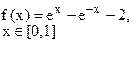 |
Окончание таблицы 3
| № вар | Исходные данные | № вар | Исходные данные | № вар | Исходные данные |
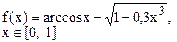 | 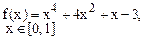 | 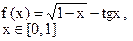 | |||
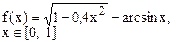 | 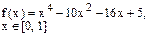 | 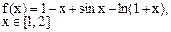 | |||
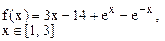 | 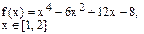 | 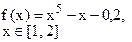 | |||
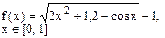 | 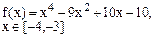 | 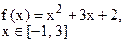 | |||
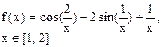 | 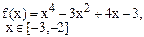 | 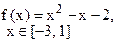 | |||
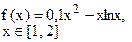 | 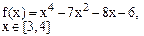 | 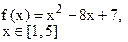 | |||
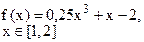 | 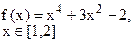 | 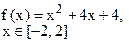 | |||
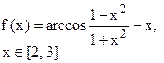 | 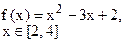 | 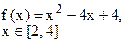 |
ЗАДАНИЕ 4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Решить систему линейных уравнений, используя различные способы.
Задание выполнить с помощью математического пакета MathCAD (использовать матричный метод, метод Гаусса, метод Крамера, встроенную функцию lsolve, метод Given-Find) и процессора электронных таблиц MS Excel (использовать матричный метод, метод Крамера, инструмент Поиск решения). Варианты заданий приведены в табл.4.
Таблица 4 – Варианты для задания 4
| № вар. | Исходные данные | № вар. | Исходные данные |
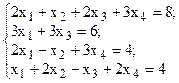 | 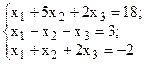 | ||
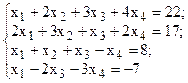 | 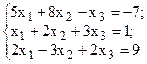 | ||
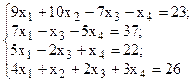 | 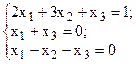 |
Продолжение таблицы 4
| № вар. | Исходные данные | № вар. | Исходные данные |
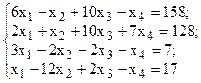 | 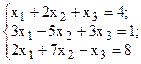 | ||
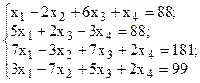 | 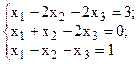 | ||
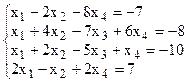 | 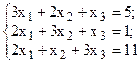 | ||
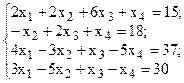 | 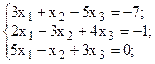 | ||
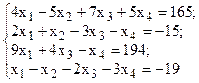 | 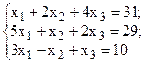 | ||
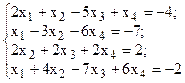 | 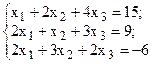 | ||
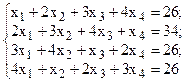 | 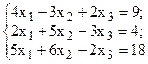 | ||
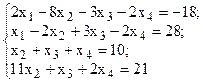 | 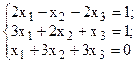 | ||
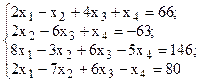 | 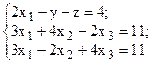 | ||
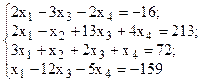 | 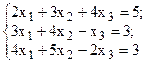 |
Окончание таблицы 4
| № вар. | Исходные данные | № вар. | Исходные данные |
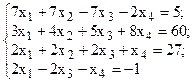 | 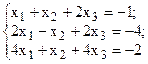 | ||
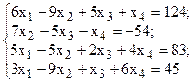 | 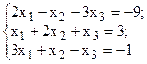 |
ЗАДАНИЕ 5. ПОСТРОИТЬ ГРАФИК ФУНКЦИЙ
А) Построить график функции, зависящей от одной переменной (декартовый график).
Б) Построить график функции, зависящей от двух переменных (поверхностный график).
Задание выполнить с помощью математического пакета MathCAD и процессора электронных таблиц MS Excel. Варианты заданий приведены в табл.5.
Таблица 5 – Варианты для задания 5
| № вар | Функция одной переменной | Функция двух переменных |
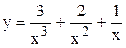 | 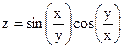 | |
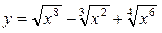 | 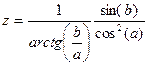 | |
| y=ln(3x)+e-3x √x | 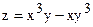 | |
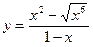 | 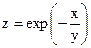 | |
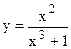 | z=4,25xe-x+6t | |
| y=sin(x)-4cos(x) | 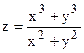 | |
| y=x2tgx | 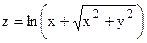 | |
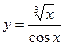 | 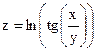 | |
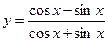 | Z=ln(x2+y2) | |
| y=(1+x2)arcos(x) | 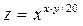 | |
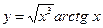 | z=(1+lg(x))y | |
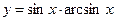 | 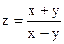 | |
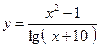 | Z=0.5 ln(x2+y2) | |
| y=xcos(x)ln(x+10) | 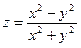 | |
| __________ y=ln(√10sin(x)+10) | 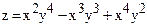 | |
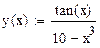 | 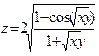 | |
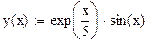 | 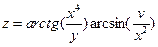 | |
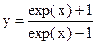 | 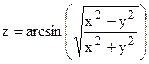 | |
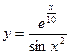 | z=(1+xy)y | |
| y=lg(3x-x) | 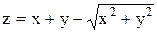 | |
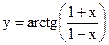 | z=sin(xy) | |
| y=cosec(x3+ex)) | 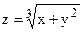 | |
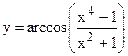 | 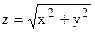 | |
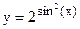 | ____ y=√ln(xy) | |
| y=cos(sin(x)) | 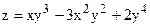 | |
| y=sec(ln(x)) | z=ex-2y | |
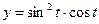 | 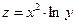 | |
| y=x2 sin (x2) | 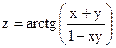 | |
| y=exp(ln2(x)) | z=yln(x) | |
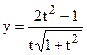 | z=ln(ex+ ey) |
