Решение линейных однородных систем дифференциальных уравнений с постоянными коэффициентами с помощью матриц (видоизмененный метод Эйлера)

Пусть дана система п линейных дифференциальных уравнений с п неизвестными функциями, коэффициенты которой постоянные:

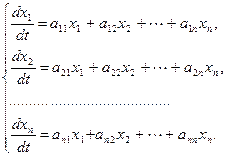
Эту систему можно записать в виде одного матричного дифференциального уравнения 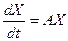, где

, , .

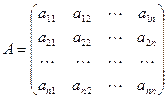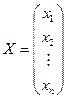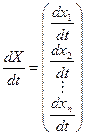Благодаря свойству собственных чисел и собственных векторов матриц 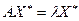,где 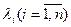-собственные числа ,а 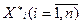- собственные векторы матрицы А, решение системы будем искать в ви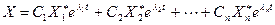де , где 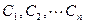-произвольные постоянные.

Чтобы найт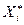и и 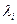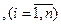решим характеристическое уравнение

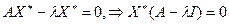,где

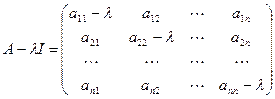
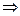
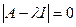
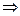
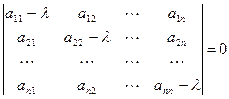
Решая данное уравнение относительно 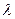,получим 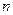корней характеристического уравнения 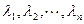,которые являются собственными числами матрицы А.Каждому собственному числу 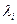соответствует собственный вектор 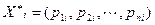.Его координаты найдем из системы уравнений

;

.

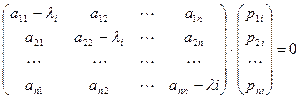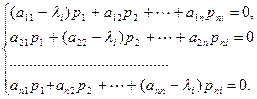Тогда решение системы запишется в виде:

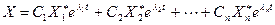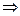; или

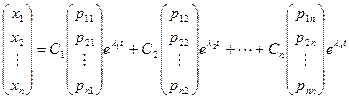
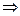
Общее решение системы имеет вид:

,

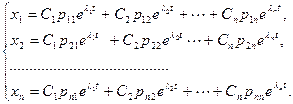Оно может быть записано иначе

,

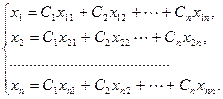где 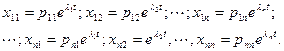- фундаментальная система решений.

Пример 13.3.Найти общее решение системы уравнений

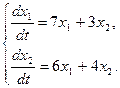
Составим характеристическое уравнение матрицы системы

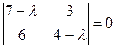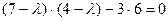; или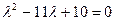

Его корни 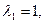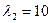-собственные ( или характеристические) числа матрицы.

При 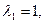уравнения для определения собственного вектора имеют вид 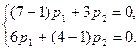и сводятся кодному уравнению .

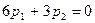Последнее определяет вектор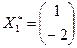

При 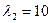получаем уравнения 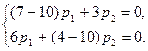или . Это уравнение определяет вектор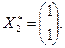

Получаем фундаментальную систему решений: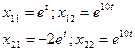

Общее решение системы имеет вид 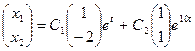или

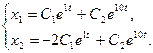
Пример 13.4. Найти общее решение системы уравнений

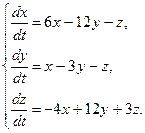
Составляем характеристическое уравнение матрицы системы:

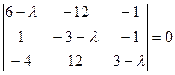
Раскрывая определитель, находим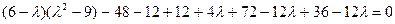

или окончательно .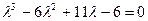

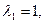
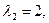
Это уравнение имеет корни 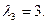Определяем собственные векторы матрицы А.

При 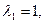получаем систему уравнений

,

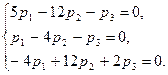одно из которых — следствие двух других.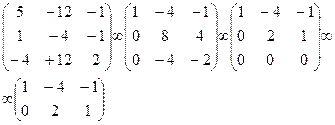

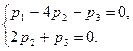данная система имеет множество решений . Отсюда , приняв 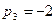, например, получим 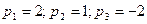.Тогда вектор .

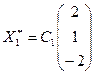При 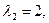имеем систему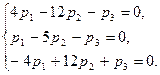

Снова используя первые два уравнения (третье— их следствие), находим

собственный вектор .

При 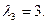имеем систему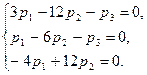

Из последнего уравнения находим 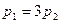. Подставляем это значение 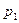в первое уравнение и находим 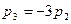. Приняв 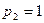, получаем 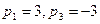, т.е. собственный вектор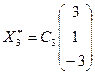

Общее решение системы имеет вид ;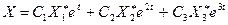

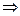
Или ,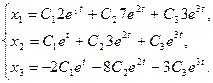

Задачи для самостоятельного решения.

Найти общее (частное) решение системы уравнений

13.1.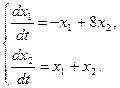

13.2.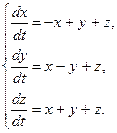

Ответы:

13.1.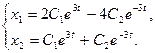

13.2.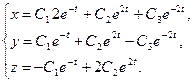

Библиографический список

1.Кузнецов М.Л., Киселев А.и,, Макаренко Г.И. и др. Вся высшая математика. т.3.М. Эдиториал УРСС. М. 2001.

2.Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах. М. Высш.шк. 1998.

3.Зарецкая М.А. Трофимова В.Ш. Шарабуряк Ю.А. Обыкновенные дифференциальные уравнения, системы уравнений. Магнитогорск. ГОУВПО МГТУ. 2006.

4.Филиппов А.Ф. Сборник задач по дифференциальным уравнениям: М.Наука 1987.