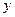Достаточное условие дифференцируемости
Если функция 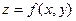 имеет частные производные в некоторой окрестности точки
имеет частные производные в некоторой окрестности точки 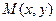 и эти производные непрерывны в точке
и эти производные непрерывны в точке 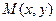 , то функция дифференцируема в этой точке. В частности, из непрерывности частных произ - водных следует непрерывность самой функции.
, то функция дифференцируема в этой точке. В частности, из непрерывности частных произ - водных следует непрерывность самой функции.
С учётом вышеизложенного, получаем новое выражение для полного дифференциала функции:
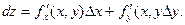 (3)
(3)
Кроме того, в силу формулы (3), 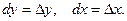
Следовательно, получаем:
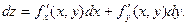 (4)
(4)
ПРИМЕР. Найти полный дифференциал функции
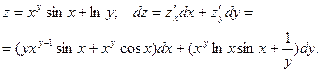
Аналогичным образом определяется дифференциал функ- ции 3-ч переменных 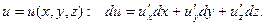
Например, для 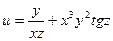 дифференциал равен:
дифференциал равен:
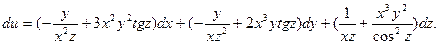
§ 4. ПРОИЗВОДНЫЕ СЛОЖНЫХ ФУНКЦИЙ
Пусть  - функция двух переменных, каждая из которых, в свою очередь является функцией независимой пе- ременной
- функция двух переменных, каждая из которых, в свою очередь является функцией независимой пе- ременной 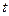 , т.е.
, т.е. 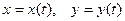 . Тогда функция
. Тогда функция 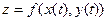 является сложной функцией переменной
является сложной функцией переменной 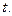 Переменные
Переменные  и
и 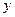 при этом называются промежуточными. Тогда выполняется следующая теорема:
при этом называются промежуточными. Тогда выполняется следующая теорема:
ТЕОРЕМА. Если функции 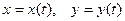 дифферен -цируемы в точке
дифферен -цируемы в точке 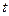 , функция
, функция 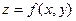 дифференцируема в точке
дифференцируема в точке 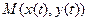 , то сложная функция
, то сложная функция 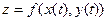 также дифференцируема в точке
также дифференцируема в точке 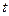 и производная этой функции (как функции одной переменной) вычисляется по формуле:
и производная этой функции (как функции одной переменной) вычисляется по формуле:
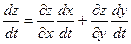 . (1)
. (1)
Замечание. Следует обратить внимание на то, что если в обозначении производной стоит 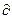 , то функция зависит от двух и более переменных, если же
, то функция зависит от двух и более переменных, если же 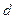 , то функция зависит только от одной переменной.
, то функция зависит только от одной переменной.
ПРИМЕРЫ. 1. Пусть 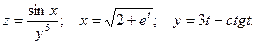
Тогда, по формуле (1),
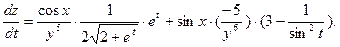
(В полученную производную вместо  и
и 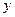 можем подставить их выражения).
можем подставить их выражения).
2. Пусть 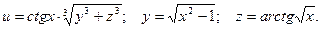
Тогда 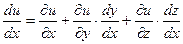 . Таким образом,
. Таким образом,
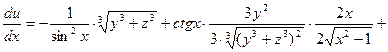
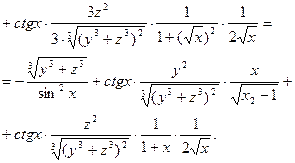
3. Пусть теперь 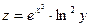 - функция двух переменных, а
- функция двух переменных, а 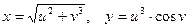 - также функции двух перемен - ных. Тогда
- также функции двух перемен - ных. Тогда  сложная функция двух переменных
сложная функция двух переменных 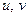 и мо -жем найти её частные производные по этим переменным сле- дующим образом:
и мо -жем найти её частные производные по этим переменным сле- дующим образом:
§ 5. ПРОИЗВОДНАЯ ОТ ФУНКЦИИ, ЗАДАННОЙ НЕЯВНО.
Пусть некоторая функция 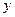 от
от  определяется уравне - нием
определяется уравне - нием 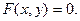 Тогда имеет место следующая теорема:
Тогда имеет место следующая теорема:
ТЕОРЕМА. Если непрерывная функция 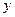 от
от  задана уравнением
задана уравнением 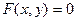 , где
, где 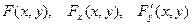 - непрерывные функции в некоторой области
- непрерывные функции в некоторой области  , причём в этой
, причём в этой
области 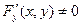 , то функция
, то функция 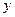 от
от  имеет производную и выполняется формула
имеет производную и выполняется формула
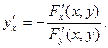 (1)
(1)
ПРИМЕР: 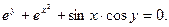 Тогда, так как левая часть равна
Тогда, так как левая часть равна 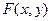 , то
, то 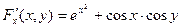 ,
,
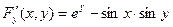 и
и 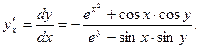
Рассмотрим теперь неявно заданную функцию двух пере -менных 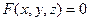 . Если считать
. Если считать  постоянной, то по фор- муле (1),
постоянной, то по фор- муле (1), 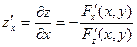 , если считать
, если считать  постоянной, то
постоянной, то 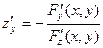 . Аналогичным образом определяются частные производные от неявно заданных функций любого числа пере- менных.
. Аналогичным образом определяются частные производные от неявно заданных функций любого числа пере- менных.
ПРИМЕРЫ.
1, 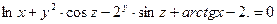 .
.
Левая часть равенства - это 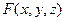 . Поэтому
. Поэтому 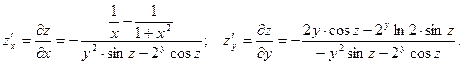
2. 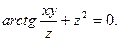 Тогда
Тогда
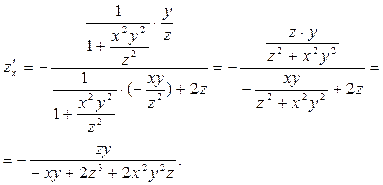
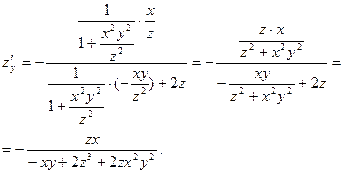
§ 6. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К
ПОВЕРХНОСТИ.
Пусть поверхность 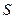 задана уравнением
задана уравнением 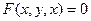 .
.
Определение 1. Касательной плоскостью к поверхности 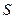 в точке
в точке 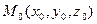 называется плоскость, которая содер –жит касательные, проведённые в точке
называется плоскость, которая содер –жит касательные, проведённые в точке 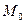 к каждой кривой, лежащей на поверхности
к каждой кривой, лежащей на поверхности 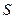 и проходящей через точку
и проходящей через точку 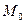 .
.
Нормальный вектор этой плоскости
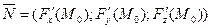 перпендикулярен к касательной каждой кривой, лежащей на поверхности
перпендикулярен к касательной каждой кривой, лежащей на поверхности  и проходящей через точку
и проходящей через точку  . Уравнение касательной плоскости имеет вид:
. Уравнение касательной плоскости имеет вид:
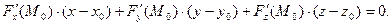
Определение 2. Нормалью называется прямая, перпендику -лярная к касательной плоскости, проходящая через точку ка –сания. Её уравнение имеет вид:
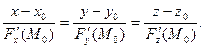
ПРИМЕРЫ:
1. Написать уравнения касательной плоскости и нормали к поверхности, проходящей через точку 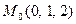 , если по - верхность
, если по - верхность 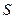 задана уравнением :
задана уравнением :
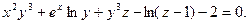
Левая часть этого равенства - это 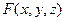 . Тогда:
. Тогда:
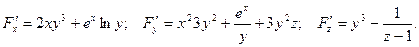
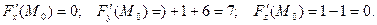
Тогда уравнение касательной плоскости имеет вид:
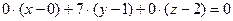 или
или 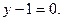
Уравнение нормали:
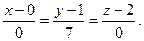
2 Написать уравнение касательной плоскости и нормали
к поверхности 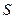 :
: 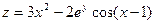 в точке
в точке 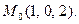
Уравнение поверхности перепишем в виде
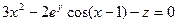 .
.
Тогда 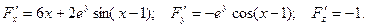
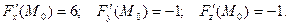 Уравнение касательной плоскости имеет вид:
Уравнение касательной плоскости имеет вид:
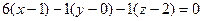 , или
, или 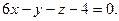
Уравнение нормали: 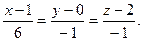
§ 7. ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ И ГРАДИЕНТ.
Рассмотрим функцию 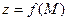 , определённую в некоторой окрестности точки
, определённую в некоторой окрестности точки 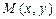 и произвольный единичный вектор
и произвольный единичный вектор 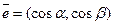

 L
L




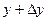
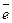
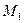
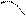
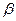

 y M
y M 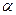
 x
x
O x x+Δx
Для характеристики скорости изменения функции в точке 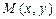 в направлении вектора
в направлении вектора 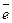 введем понятие производ- ной по направлению. Для этого через точку
введем понятие производ- ной по направлению. Для этого через точку 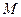 проведём пря- мую
проведём пря- мую 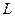 так чтобы её направление совпадало с направлением ыектора
так чтобы её направление совпадало с направлением ыектора 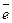 и на направленной прямой выберем точку
и на направленной прямой выберем точку 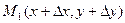 . Если
. Если 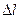 - длина отрезка
- длина отрезка 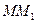 , то
, то 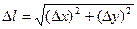 . При этом функция
. При этом функция 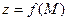 получает приращение
получает приращение 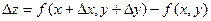 .
.
Определение 1. Предел отношения 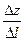 при
при 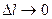 (
( 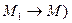 , если он существует, называется производной функции
, если он существует, называется производной функции 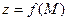 в точке
в точке 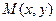 по направлению вектора
по направлению вектора 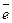 и обозначается
и обозначается 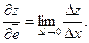
Если функция 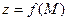 дифференцируема в точке
дифференцируема в точке 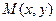 , то её приращение вдоль прямой
, то её приращение вдоль прямой 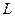 можно представить в виде:
можно представить в виде:
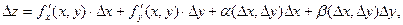 где
где 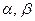 - бесконечно малые функции при
- бесконечно малые функции при 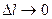 . Разде –лим обе части последнего равенства на
. Разде –лим обе части последнего равенства на 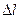 . Тогда, принимая во внимание, что
. Тогда, принимая во внимание, что 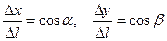 , имеем:
, имеем: 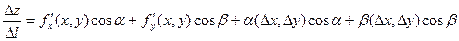 и при переходе в этом равенстве при
и при переходе в этом равенстве при 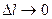 , получаем формулу
, получаем формулу
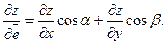 (1)
(1)
Если же 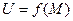 - функция трёх переменной, определён- ная в некоторой окрестности точки
- функция трёх переменной, определён- ная в некоторой окрестности точки 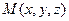 , а
, а 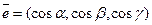 , где
, где 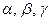 - углы, образованные век- тором с соответствующими осями координат - произвольный единичный вектор в пространстве, определяющий некоторое направление, производная функции
- углы, образованные век- тором с соответствующими осями координат - произвольный единичный вектор в пространстве, определяющий некоторое направление, производная функции 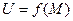 или, что то же самое, скалярного поля
или, что то же самое, скалярного поля 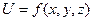 вычисляется по формуле
вычисляется по формуле
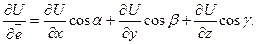 (2)
(2)
ПРИМЕРЫ
1. Пусть 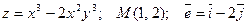 . Найти про - изводную скалярного поля
. Найти про - изводную скалярного поля 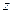 в точке
в точке 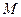 в направлении вектора
в направлении вектора 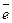 .
. 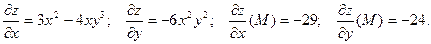
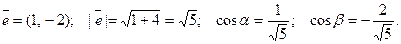 Тогда, по формуле (1),
Тогда, по формуле (1), 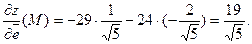
2. 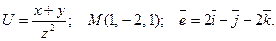 Найти в точке
Найти в точке 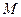 производную скалярного поля
производную скалярного поля 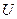 в направлении вектора
в направлении вектора 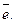
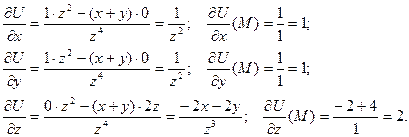
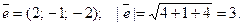 Тогда направляющие ко -синусы вектора
Тогда направляющие ко -синусы вектора 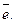 :
: 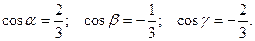
Следовательно, по формуле (2)
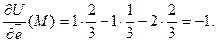
Определение 2. Градиентом функции  в точке
в точке 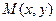 называется вектор, координаты которого равны соответствующим частным производным
называется вектор, координаты которого равны соответствующим частным производным 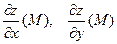 .
.
Таким образом, 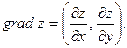 (4)
(4)
Если вспомним формулу производной по направлению, получим
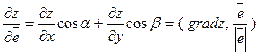 (5)
(5)
Но, по определению скалярного произведения, имеем

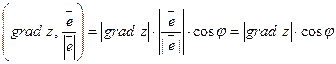 . (6)
. (6)
Здесь 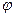 - угол между вектором
- угол между вектором 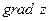 и единичным векто - ром направления
и единичным векто - ром направления 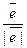 . Из равенства (6) следует, что произ -водная функции по направлению имеет наибольшую величину при
. Из равенства (6) следует, что произ -водная функции по направлению имеет наибольшую величину при 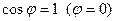 , т.е. когда направление вектора совпа -дает с направлением
, т.е. когда направление вектора совпа -дает с направлением 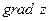 .
.
Замечание: Вектор 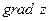 показывает направление максимального изменения функции, а его длина
показывает направление максимального изменения функции, а его длина 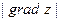 равна скорости максимального изменения.
равна скорости максимального изменения.
Если 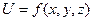 функция трёх переменных и
функция трёх переменных и 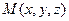 , то
, то 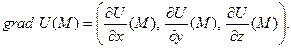 (7)
(7)
ПРИМЕРЫ:
1. Пусть 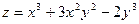 . Найти
. Найти 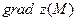 , где
, где 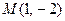 .
.
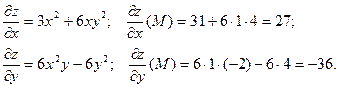
Тогда, ,по формуле (4), 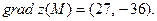
3. Найти наибольшую скорость возрастания функции
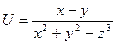
 в точке
в точке 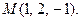
Найдём 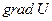 .
.
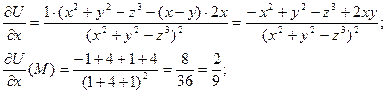
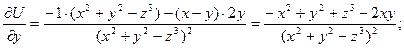
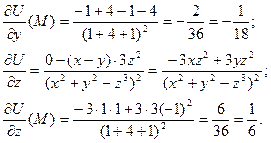
Тогда 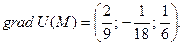 Его длина равна скорости наибольшего изменения функции
Его длина равна скорости наибольшего изменения функции 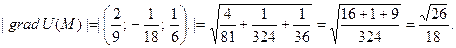
§ 8. ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ.
Пусть в некоторой окрестности точки 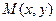 существуют частные производные функции
существуют частные производные функции 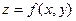 :
: 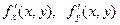 , которые сами являются функциями двух переменных
, которые сами являются функциями двух переменных  и
и 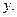 Назовём их частными производными 1-го порядка.
Назовём их частными производными 1-го порядка.
Частные производные от этих функций по переменным  и
и 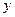 , если они существуют, называются частными производными второго порядка и обозначаются следующим образом:
, если они существуют, называются частными производными второго порядка и обозначаются следующим образом:
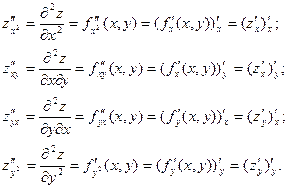
Частные производные 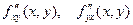 называются сме- шанными частными производными. Для них имеет место сле -дующая теореме:
называются сме- шанными частными производными. Для них имеет место сле -дующая теореме:
ТЕОРЕМА. Если производные 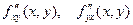 сущест- вуют в некоторой
сущест- вуют в некоторой 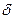 - окрестности точки
- окрестности точки 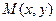 и непрерыв- ны в самой точке
и непрерыв- ны в самой точке 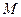 , то они равны между собой, т.е. имеет место равенство:
, то они равны между собой, т.е. имеет место равенство: 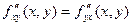 .
.
Аналогичным образом можно ввести понятия частных про- изводных 3-го и более высоких порядков и частные произ -водные высших порядков для функция трёх и более пере -менных.
Теорема остаётся верной и для производных более высокого порядка. Например 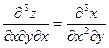 и т.д.
и т.д.
ПРИМЕРЫ:
1. Доказать равенство 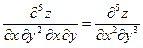 для функции
для функции 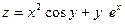
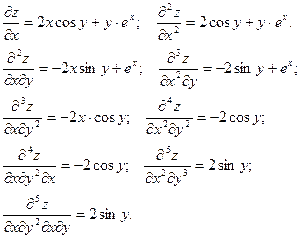
Таким образом, равенство доказано.
2. Пусть 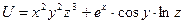 . Проверить, что выполняется равенство:
. Проверить, что выполняется равенство: 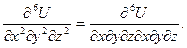
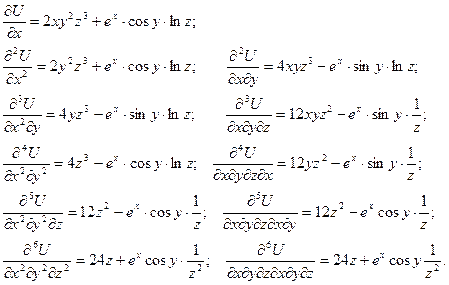 Как видим, в этом случае равенство также выполняется.
Как видим, в этом случае равенство также выполняется.
§ 9. ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ.
Пусть функция 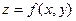 определена в некоторой окрестности
определена в некоторой окрестности 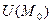 точки
точки 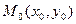 .
.
Определение 1. Говорят, что функция 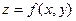 имеет в точке
имеет в точке 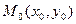 локальный максимум, если существует какая окрестность этой точки
локальный максимум, если существует какая окрестность этой точки 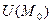 , что для всех точек
, что для всех точек 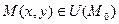 выполняется неравенство
выполняется неравенство
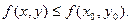 (1)
(1)
Если, при тех же условиях выполняется противоположное неравенство 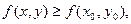 то говорят, что в точке
то говорят, что в точке 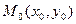 функция имеет локальный минимум. Точки локального максимума и минимума называются точками экстремума.
функция имеет локальный минимум. Точки локального максимума и минимума называются точками экстремума.
Из определения следует, что если функция 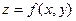 имеет экстремум в точке
имеет экстремум в точке 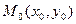 , то в окрестности точки полное приращение функции
, то в окрестности точки полное приращение функции
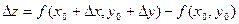
имеет вполне определённый знак, а именно, 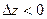 в окрест -ности точки максимума и
в окрест -ности точки максимума и 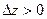 в окрестности точки миниму –ма.
в окрестности точки миниму –ма.
Необходимое условие экстремума.
Если функция 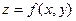 имеет экстремум в точке
имеет экстремум в точке 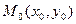 и имеет в некоторой окрестности этой точки частные производные первого порядка, то эти производные обращаются в ноль в точке
и имеет в некоторой окрестности этой точки частные производные первого порядка, то эти производные обращаются в ноль в точке 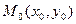 , т.е.
, т.е.
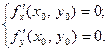
 (2)
(2)
Точки, в которых выполняются условия (2), называются
стационарными точками, или точками возможного экстремума.
Другими словами, условия (2) не достаточны для существова -ния экстремума в точке 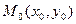 .
.
Достаточное условие экстремума..
Пусть 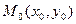 - стационарная точка, т.е. для неё выполнены условия (2). Пусть, далее в некоторой окрестности этой точки функция
- стационарная точка, т.е. для неё выполнены условия (2). Пусть, далее в некоторой окрестности этой точки функция 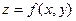 имеет частные производные второго порядка, непрерывные в точке
имеет частные производные второго порядка, непрерывные в точке 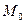 Пусть
Пусть
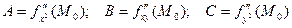 .
.
Положим:
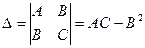 . (3)
. (3)
Если 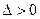 , то функция имеет экстремум в точке
, то функция имеет экстремум в точке 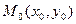 , причём, если
, причём, если 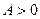 , то минимум, если
, то минимум, если 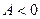 - максимум; если
- максимум; если 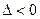 , то в точке
, то в точке 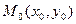 функция не имеет экст- ремума; если
функция не имеет экст- ремума; если 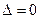 , то признак ответа не лаёт и необходимо дальнейшее исследование.
, то признак ответа не лаёт и необходимо дальнейшее исследование.
ПРИМЕРЫ: Найти экстремумы следующих функций:
1. 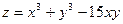 .
.
Найдём стационарные точки:
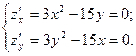 Тогда
Тогда 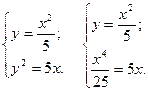
Решаем второе уравнение: 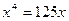 , или
, или 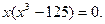
Тогда 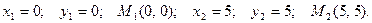
Исследуем обе точки на экстремум, пользуясь достаточным условием экстремума. Для этого найдём вторые производные:
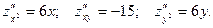
Для точки 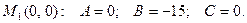 Тогда, по формуле (3),
Тогда, по формуле (3), 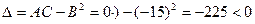 и в этой точке нет экстремума функции.
и в этой точке нет экстремума функции.
Для точки 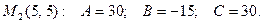 Тогда
Тогда
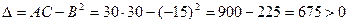 и в этой точке функция имеет экстремум, причём, так как
и в этой точке функция имеет экстремум, причём, так как 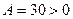 , то в точке
, то в точке  функция имеет минимум и
функция имеет минимум и
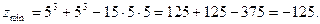
2. 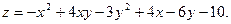
Ищем стационарные точки:
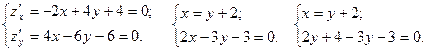
Тогда 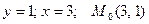 - стационарная точка. Исследуем эту точку на экстремум по достаточному признаку:
- стационарная точка. Исследуем эту точку на экстремум по достаточному признаку: 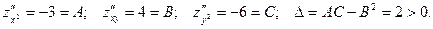 Следовательно, в точке
Следовательно, в точке 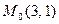 функция имеет экстремум, причём, так как
функция имеет экстремум, причём, так как 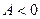 , то максимум.
, то максимум.
§ 10. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЕ
ФУНКЦИИ В ЗАМКНУТОЙ ОБЛАСТИ.
Пусть функция 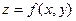 определена и непрерывна в не- которой замкнутой области
определена и непрерывна в не- которой замкнутой области  на плоскости. Тогда наибольшее и наименьшее значение в этой области функция может прини- мать либо в стационарных точках, попадающих в область, ли -бо на границе области. Правила нахождения наибольшего и наименьшего значения лучше рассмотреть на примерах.
на плоскости. Тогда наибольшее и наименьшее значение в этой области функция может прини- мать либо в стационарных точках, попадающих в область, ли -бо на границе области. Правила нахождения наибольшего и наименьшего значения лучше рассмотреть на примерах.
ПРИМЕРЫ. Найти наибольшее и наименьшее значение функции 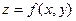 в замкнутой области
в замкнутой области  .
.
1. 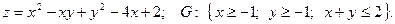

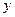



 С 3
С 3
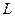
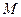

 -1 0 2 3
-1 0 2 3 


 -1 К А
-1 К А
Сначала найдём стационарную точку:
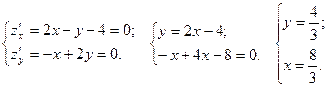
Точка 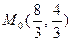 не попадает в область
не попадает в область  . Найдём критические точки на границе области
. Найдём критические точки на границе области  . На участке
. На участке 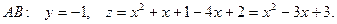 Тогда
Тогда
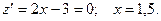 Точка
Точка 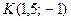 лежит на отрезке
лежит на отрезке 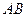 границы области
границы области  . На участке
. На участке 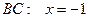 . Тогда
. Тогда 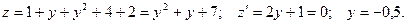
Точка 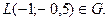 На третьем участке
На третьем участке 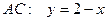 , тогда
, тогда 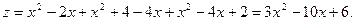
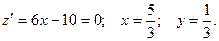 Точка
Точка 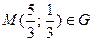 .
.
Таким образом мы нашли три точки, в которых функция мо -жет принять экстремальные значения. Кроме того необходимо ещё учесть угловые точки 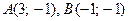 ,
,  . В каждой из этих точек найдём значение функции:
. В каждой из этих точек найдём значение функции:
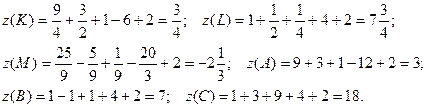 Итак, наибольшее значение функции в области
Итак, наибольшее значение функции в области  :
: 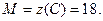 Наименьшее значение функции в области
Наименьшее значение функции в области  :
:
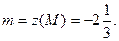
2. 

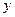
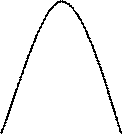 4 С
4 С


 -3 -2
-3 -2  2 3
2 3 

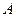 -5
-5 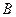

Найдём стационарные точки:
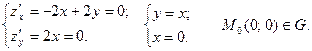
Найдём критические точки на границе области 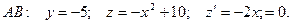 Точка
Точка 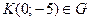

На участке 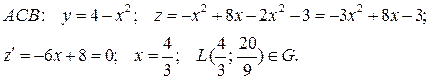
Кроме того, нужно ещё рассмотреть угловые точки:
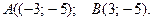
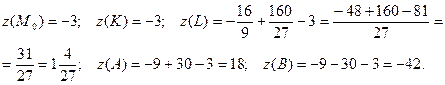
Таким образом, самое большое значение 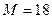 функция принимает в точке
функция принимает в точке  ; самое маленькое значение
; самое маленькое значение 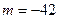 - в точке
- в точке  .
.
КРАТНЫЕ ТНТЕГРАЛЫ.
§ 1.ДВОЙНЫЕ ИНТЕГРАЛЫ.
Пусть  - замкнутая, ограниченная область в плоскости
- замкнутая, ограниченная область в плоскости 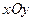 , а
, а 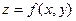 - функция, определённая и ограниченная в точках области
- функция, определённая и ограниченная в точках области  .
.
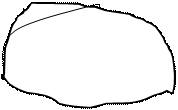
Разобьём область  на
на 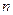 частей
частей 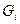 с площадями
с площадями 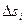 , не имеющих общих внутренних точек. В каждой частичной области
, не имеющих общих внутренних точек. В каждой частичной области 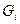 возьмём произвольную точку
возьмём произвольную точку 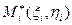 и составим сумму
и составим сумму







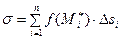 , (1) которую назовём интегральной суммой для функции
, (1) которую назовём интегральной суммой для функции 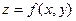 в области
в области  .
.


 |

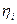
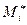
О 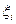

Диаметром области  -
- 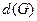 - называемся наибольшее расстояние между граничными точками области
- называемся наибольшее расстояние между граничными точками области  . Пусть
. Пусть 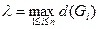 .
.
Определении 1. Если интегральная сумма (1) при 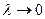 имеет конечный предел
имеет конечный предел 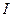 , то этот предел называется двой -ным интегралом от функции
, то этот предел называется двой -ным интегралом от функции 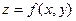 по области
по области  и обозначается:
и обозначается:
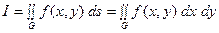 . (2)
. (2)
В этом случае функция 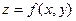 называется интегри- руемой в области
называется интегри- руемой в области  ,
,  называется областью интегриро-вания, а
называется областью интегриро-вания, а 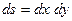 - элементом площади.
- элементом площади.
Если функция 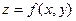 непрерывна (или кусочно - непре- рывна) в области
непрерывна (или кусочно - непре- рывна) в области  , то она интегрируема в этой области.
, то она интегрируема в этой области.
Геометрический смысл двойного интеграла:  Двойной интеграл численно равен объёму криволинейного цилиндра, ограниченного сверху графиком неотрицательной функции
Двойной интеграл численно равен объёму криволинейного цилиндра, ограниченного сверху графиком неотрицательной функции 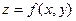 ; снизу - областью
; снизу - областью  , лежащей в плоскости
, лежащей в плоскости 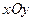 , а с боковых сторон - цилиндрической поверхностью, обра -зующая которой параллельна оси
, а с боковых сторон - цилиндрической поверхностью, обра -зующая которой параллельна оси 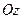 , а направляющая - совпадает с границей области
, а направляющая - совпадает с границей области  .
.

 |
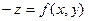
 |

 | |||||||||||||||||
 | |||||||||||||||||
 |  |  |  |  |  |  | |||||||||||

 О
О