Лабораторная работа №13

1. Решить задачу Коши для уравнения первого порядка на одном и том же множестве значений 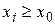с шагом 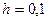и ., и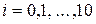спользуя метод Эйлера первого порядка, исправленный или модифицированный метод Эйлера и метод Рунге-Кутта 4-го порядка Полученные результаты свести в одну таблицу и сопоставить.

2. Используя метод Эйлера с уточнением, найти приближенное решение задачи Коши в тех же точках, что и в предыдущем задании. Точность вычислений должна составить 0,0001. Помимо решения в каждой точке вывести число итераций.

1. , .

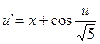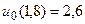2. , .

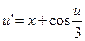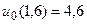3. , .

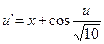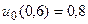4. , .

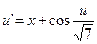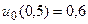5. , .

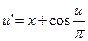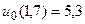6. , .

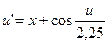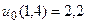7. , .

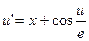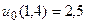8. , .

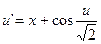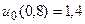9. , .

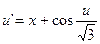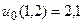10. , .

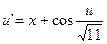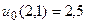11. , .

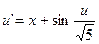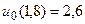12. , .

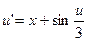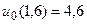13. , .

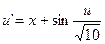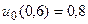14. , .

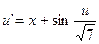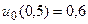15. , .

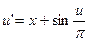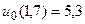16. , .

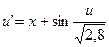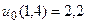17. , .

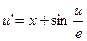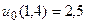18. , .

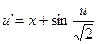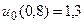19. , .

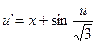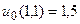20. , .

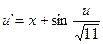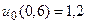21. , .

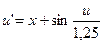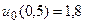22. , .

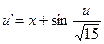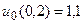23. , .

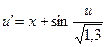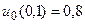24. , .

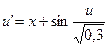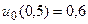25. , .

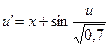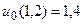26. , .

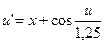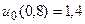27. , .

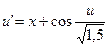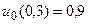28. , .

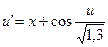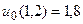29. , .

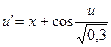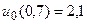30. , .

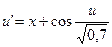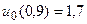Лабораторная работа №14

Используя метод Рунге-Кутта 4-го порядка, найти приближенное решение 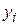и 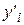задачи Коши для дифференциального уравнения второго порядка при 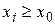с шагом 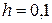на отрезке 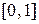, удовлетворяющее начальным условиям , .

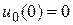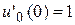1. ,

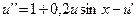2. ,

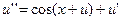3. ,

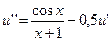4. ,

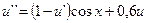5. ,

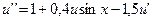6. ,

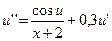7. ,

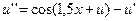8. ,

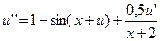9. ,

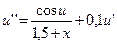10. ,

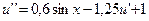11. ,

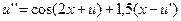12. ,

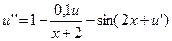13. ,

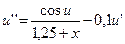14. ,

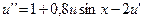15. ,

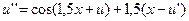16. ,

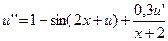17. ,

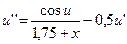18. ,

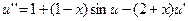19. ,

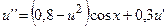20. ,

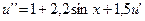21. ,

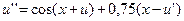22. ,

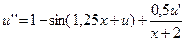23. ,

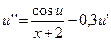24. ,

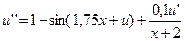25. ,

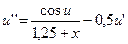26. ,

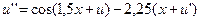27. ,

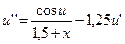28. ,

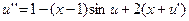29. ,

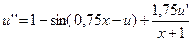30.

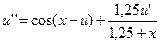
Краевая задача для линейного дифференциального уравнения

Второго порядка

В общем виде краевая задача записывается с помощью уравнения

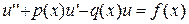при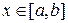

и его краевых условий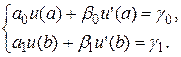

Здесь 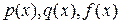- заданные функции, 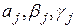- коэффициенты ( 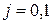). Необходимо найти решение этой задачи 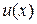на отрезке .

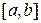В частных случаях( ):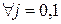

1. 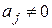, 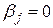- краевое условие первого рода (условие Дирихле)

2. 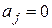, 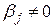- краевое условие второго рода (условие Неймана)

3. 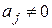, 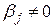- краевое условие третьего рода (смешанное краевое условие)

Область интегрирования разбивается на N отрезков длиной (шагом) 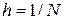, тогда 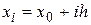, i=0,…,N. заданные функции в узловых точках заменяются на 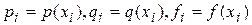. Первая производная в уравнении аппроксимируется центральным конечно-разностным отношением: 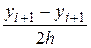, вторая - отношением .

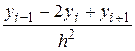В результате задача сводится к конечно разностному уравнению

, ,

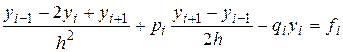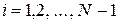которое легко сводится к виду

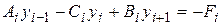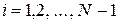, , где

, , , .

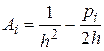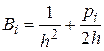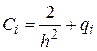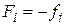Данное уравнение решается методом прогонки (так же как это было рассмотрено для сплайн-интерполяции).

Прогоночные коэффициенты вычисляются по рекуррентным формулам:

, , .

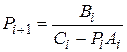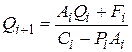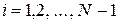Значения 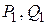определяются из конечно-разностной формы первого краевого условия: 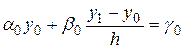. Отсюда:

, .

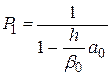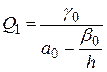Из второго краевого условия 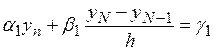и формулы 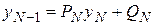определятся

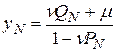, где , .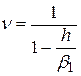

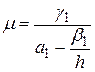По формуле 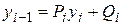для i=N, N-1, …, 2, 1 находятся все остальные значения .

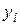Лабораторная работа №15

С помощью метода конечных разностей, найти приближенное решение краевой задачи для обыкновенного дифференциального уравнения второго порядка с точностью 10^-6 и шагом .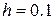

1. ,

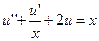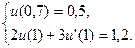
2. ,

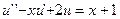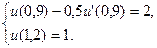
3. ,

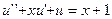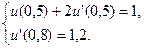
4. ,

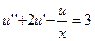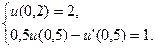
5. ,

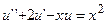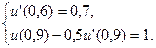
6. ,

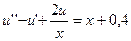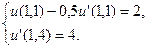
7. ,

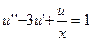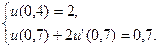
8. ,

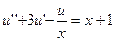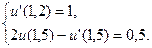
9. ,

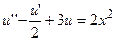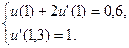
10. ,

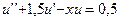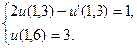
11. ,

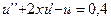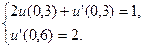
12. ,

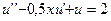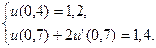
13. ,

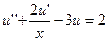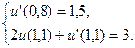
14. ,

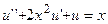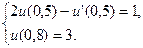
15. ,

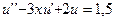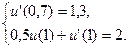
16. ,

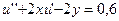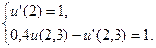
17. ,

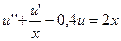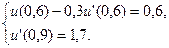
18. ,

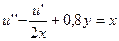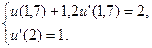
19. ,

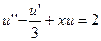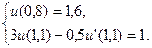
20. ,

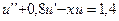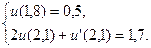
21. ,

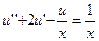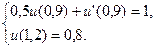
22. ,

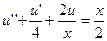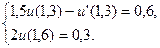
23. ,

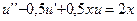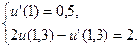
24. ,

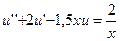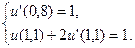
25. ,

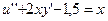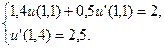
26. ,

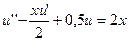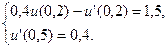
27. ,

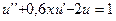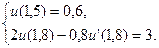
28. ,

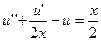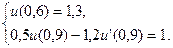
29. ,

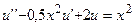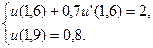
30. ,

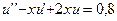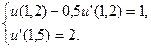
Физическая задача №4

Методом пошагового интегрирования найти зависимость тока от времени J(t) и параметры этой зависимости. Ток течет в колебательном контуре, содержащем емкость C, индуктивность L и сопротивление R. При постоянных значениях параметров контура имеется точное решение, описывающее процесс затухающих колебаний. Это решение рекомендуется использовать для проверки схемы счета и оценки погрешности решения. Полагается, что сопротивление цепи R увеличивается за счет выделения на нем тепла по закону Джоуля-Ленца. Дифференциальное уравнение задачи имеет вид:

L× dJ/dt + R×J + q /C = 0 (1)

Это уравнение отражает второй закон Кирхгофа для замкнутой цепи – сумма падений напряжений равна сумме ЭДС (ЭДС в нашей цепи нет). Первое слагаемое в (1) - падение напряжения на индуктивности U_L, второе слагаемое – падение напряжения на пассивном сопротивлении U_R (закон Ома), третье слагаемое – напряжение на емкости U_C (q -величина заряда на емкости). Используя связь тока с изменением заряда на конденсаторе J = dq/dt, уравнение (1) записывают в виде:

d²q/dt² + 2×b×dq/dt + w₀²×q = 0, (2)

в котором использованы обозначения для декремента затухания и собственной частоты:

b = 0.5R/L, w₀² = 1/(L×C) . (3)

При b = 0 дифференциальное уравнение описывает гармонические колебания с циклической частотой w₀ (циклическая частота равна обычной частоте умноженной на 2p). При b = const < w₀ происходят затухающие колебания с частотой 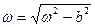(если b > w₀ колебания ангармонические). Напомним, что в нашем случае b ¹ const.

Перейдем к описанию способа вычисления сопротивления R(T) = R(T(t)). При небольших изменениях температуры полагают, что сопротивление линейно зависит от температуры:

R(T) = R(0) (1+ a(T - T₀)) (4)

В этой зависимости R(0) - сопротивление при температуре T₀ , а a - температурный коэффициент. Для нахождения температуры полагаем, что все тепло, выделившееся на сопротивлении согласно закона Джоуля-Ленца

Q(t) = ò J²(t)×R(t)×dt » t×åJ_k² R_k (5)

идет на нагрев сопротивления в соответствии с формулой

Q = m×c×(T – T₀), (6)

в котором m - масса сопротивления, а с – теплоемкость единицы массы. Из формул (5)-(6) следует, что

T(t) » T₀ + (t×åJ_k² R_k )/(m×c). (7)

Сумма в (7) соответствует приближенному вычислению интеграла по методу прямоугольников (t- шаг по времени, k - номер шага по времени).

Опишем простейшую схему счета (можно использовать другую, но иметь ²доказательства² ее работоспособности) с порядком аппроксимации O(t²):

q_k+1 - 2×q_k + q_k-1 + b×t×(q_k+1-q_k-1) + (t×w₀)²q_k =0. (8)

После преобразований схема приводится к виду:

q_k+1 = ((2 - (t×w₀)²)×q_k + (t×b_k –1)×q_k-1)/(1+t×b_k) (9)

Обсудим начальные условия задачи. В начальный момент времени полагается, что ток не течет, а на конденсаторе задается разность потенциалов U₀. То есть предполагается, что начальный момент времени соответствует моменту включения в цепь заряженного конденсатора. Таким образом, имеем:

q(0) = C×U₀, J(0) = 0 (10)

Для счета по трехслойной схеме требуются значения заряда на двух слоях. Одно значение при k = 0 следует из (10). Значение при k=1 (t=t) находится из разложения q(t) в ряд Тейлора и использования дифференциального уравнения вместе с начальным условием для тока:

q₁ = q₀×(1 – 0.5×t²×w₀²) (11)

К числу фиксированных параметров относятся (используется система единиц СИ):

C = 440 мкФ , L = 4×10^-7 Гн, с=0.896 кДж/(кг К),

R(0)= 10^-4 Ом, m = 1 г , Т₀ = 20 °С, (12)

Тпл=660.1 °С, Qпл=397 к Дж/кг, 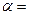0.0043/К.

Электрические параметры примерно соответствуют параметрам, которые использовались при попытках превращения графита в алмаз в лаборатории радиоспектроскопии А.С. Кимом. Графит находился в металлической обойме, которая при протекании тока расплавлялась и за счет пинч-эффекта сжимала графит. Параметры металлической обоймы (m, с, 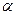, Тпл, Qпл) соответствуют алюминию [1].

Начальное напряжение на конденсаторе определяется номером студента по формуле 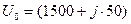В.

Условия представления и защиты результатов.

1.Разбираться в физической и математической постановке задачи. Счет вести в течении периода 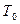, определенного по циклической частоте .

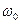2. Показать зависимость интегральных характеристик решения от основного параметра метода -t. В качестве интегральных характеристик выбрать первое экстремальное значение силы тока и время достижения этого значения.

3. Представить зависимости J(t), Т(t) на периоде 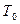. Объяснить их. Выяснить – достигнута ли температура плавления. Указать погрешности выбранной модели.

Физическая задача №5

Требуется решить стационарное одномерное уравнение теплопроводности:

(l×T¢)¢ + Q(T) = 0. (1)

В этом уравнении Т(x) – температура, l - коэффициент теплопроводности, Q – мощность источников тепла. Уравнение решается при граничных условиях первого рода

Т(0) = Т(L) = T₀ = 20°C (2)

Полагается, что внутренние источники тепла обязаны протеканию постоянного тока J по металлическому проводнику длиной - L, сечением - S и удельным сопротивлением r = r(Т). В этом случае

Q(x) = r(T)×J² /S², r(T) = r(T₀)×(1+a×(T – T₀)) (3)

Величина постоянного тока определяется из закона Ома

J = U₀/R(T), R(T) = (òr(T(x))×dx)/S. (4)

Коэффициент теплопроводности в (1) будем считать постоянным. В этом случае уравнение (1) c учетом принятых допущений приводится к виду

T¢¢ + U₀²×S^-2×r(T)/(lR²(T)) = 0. (5)

Как видно, это нелинейное уравнение. Решать соответствующие ему конечно-разностные уравнения логично с помощью итераций

T_k+1^(m+1) – 2 T_k^(m+1) +T_k-1^(m+1) + h²× F(T^(m)) =0. (6)

В этом уравнении F(T^(m)) соответствует внутренним источникам тепла в уравнении (5), h – шаг пространственной сетки (h = L/N), k – номер узла. На каждой итерации уравнение (6) решается методом скалярной прогонки. Интеграл, определяющий общее сопротивление проводника длиной L, считать по любой квадратурной формуле (метод прямоугольников или метод трапеций). Проверку метода прогонки можно осуществить на варианте с точным решением, считая, что удельное сопротивление не зависит от температуры. В этом случае уравнение (5) приводится к виду (q – const)

T¢¢ + q = 0, q = U₀²¤(l×r(0)×L²). (7)

Точное решение этого уравнения

T = T₀ + 0.5×q×x×(L-x). (8)

Заданными параметрами считать

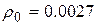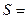L = 10 см, Т₀ =20°С , Ом мм /м ,

2 мм 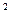, 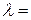209 Вт/(м К) (9)

Задаваемым параметром является величина напряжения источника тока в вольтах 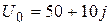( 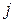- номер студента в группе).

Условия представления и защиты результатов.

1. Разбираться в физической и математической постановке задачи. Указать погрешности выбранной модели.

2. Показать зависимость результатов от основного параметра метода – h и от числа итераций. В качестве интегральной характеристики выбрать максимальное значение температуры, достигаемое в середине проводника при .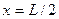

3. Представить зависимость T(x), сравнить ее с зависимостью при постоянном значении мощности источника и объяснить различие.

Комментарий. При использовании данных обратить внимание на единицы. Так, например, значение r в единицах Ом×мм²¤м требуется умножением на 10^-6 перевести в Ом×м.