Методом скоростного градиента
Цель работы: исследование свойств системы стабилизации, в которой коэффициенты регулятора изменяются по алгоритму скоростного градиента в конечно-дифференциальной форме.
Основные сведения
Суть метода скоростного градиента заключается в следующем: настройка параметров осуществляется в направлении, противоположном скорости изменения целевого функционала вдоль траектории обобщенного настраиваемого объекта (ОНО). Алгоритмом скоростного градиента (АСГ) называется правило изменения вектора настраиваемых коэффициентов (q), задаваемое уравнением вида
 (2.1)
(2.1)
где Ñ – дифференциальный оператор, Г = ГТ > 0 – квадратная матрица коэффициентов передачи,

здесь Q(.) – целевой функционал; f(x, q, t) – вектор-функция, описывающая ОНО,

y(.) – некоторая вектор-функция, удовлетворяющая условию псевдоградиентности

АСГ вида (2.1) называют алгоритмом в конечно-дифференциальной форме. Частным случаем (2.1) являются алгоритмы в дифференциальной форме (в случае y = 0)
 (2.2)
(2.2)
и в конечной форме (для Г = 0)
 ,
,
где g – шаг дискретизации.
Рассмотрим пример синтеза системы с параметрической адаптацией. Объект управления задан моделью в пространстве состояний
 (2.3)
(2.3)
где xÎRn, u ÎRm – векторы состояния и входа ОУ; А, B – неизвестные матрицы коэффициентов.
Эталонная модель выбрана в форме
 (2.4)
(2.4)
где rÎRm – задающее воздействие; Ам – гурвицева матрица.
Цель управления сформирована относительно координатного рассогласования
 (2.5)
(2.5)
где e (t) = x (t) – xм(t). Предлагаем выполнение условия управляемости объекта и наблюдаемости координат состояния.
Пусть целевой функционал выбран в форме скалярной квадратичной функции
 (2.6)
(2.6)
Поставленная цель управления выполняется, если Q ® 0 при t ® ¥.
Уравнение основного контура можно получить модальным методом, т.е. разрешив уравнение

относительно u (t):
 ,
,
или
 . (2.7)
. (2.7)
«Идеальное» управление можно записать в форме
 (2.8)
(2.8)
где матрицы k*x, k*r удовлетворяют условию


 . (2.9)
. (2.9)
Матрицы идеальных значений коэффициентов регулятора k*x, k*r существуют, если выполняются ранговые условия

Реальный закон управления имеет вид
 (2.10)
(2.10)
где kx(t), kr(t) – матрицы настраиваемых коэффициентов регулятора, 
Для определения вида алгоритма адаптации требуется вычислить производную целевого функционала (2.6) в силу уравнений системы (2.3), (2.4), (2.10):
 (2.11)
(2.11)
После подстановки (2.10) в (2.11) имеем

 . (2.12)
. (2.12)
Определим скоростные градиенты
 ,
,
 .
.
Для алгоритмов настройки коэффициентов выбираем АСГ в дифференциальной форме (2.2)
 (2.13)
(2.13)
где Г = g I, g > 0.
Система (2.3), (2.4), (2.10), (2.13) относится к системам с параметрической адаптацией. На основе АСГ можно синтезировать системы с сигнальной и сигнально- параметрической адаптацией. Системы с алгоритмом адаптации (2.13) сохраняют работоспособность при изменении координатных и параметрических возмущений в широких пределах. Качество процессов ухудшается, если скорость изменения параметрических возмущений высокая.
С целью повышения быстродействия в контурах параметричес-
кой настройки коэффициентов регулятора можно применять пропор-ционально-интегральные алгоритмы адаптации в дифференциальной форме:

 (2.14)
(2.14)
Методические указания
Рассматривается линейный одноканальный объект управления (1.18), (1.19) с параметрическими возмущениями. Желаемая динамика системы задана уравнением эталонной модели (1.20) по требованиям к качеству переходных процессов (табл. 1.1). В системе эталонная модель реализуется в виде линейного динамического звена. Согласно методу эталонного уравнения получим описание регулятора:
 , (2.15)
, (2.15)
или
 , (2.16)
, (2.16)
где  =
= 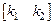 ,
,  ,
, 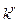 – настраиваемые коэффициенты регулятора, изменение которых осуществляется по пропорционально-интег-ральному алгоритму (2.14):
– настраиваемые коэффициенты регулятора, изменение которых осуществляется по пропорционально-интег-ральному алгоритму (2.14):
 =
=  , (2.17)
, (2.17)
 , (2.18)
, (2.18)
где  ,
,  – матрица коэффициентов, удовлетворяющая уравнению Ляпунова
– матрица коэффициентов, удовлетворяющая уравнению Ляпунова
 = – D. (2.19)
= – D. (2.19)
Уравнения (2.17), (2.18) можно записать в виде
 , (2.20)
, (2.20)
 , (2.21)
, (2.21)
 . (2.22)
. (2.22)
Дифференциальные уравнения (2.17), (2.18) или (2.20)–(2.22) описывают адаптор, структурная схема которого изображена на рис. 2.1.

Рис. 2.1
Быстродействие адаптора определяется с помощью времени сходимости процессов (  ), которое определяется аналогично
), которое определяется аналогично 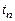 , но по графикам
, но по графикам  i – индекс настраиваемого коэффициента регулятора. В случае пятипроцентных отклонений область установившихся значений коэффициентов задается неравенством
i – индекс настраиваемого коэффициента регулятора. В случае пятипроцентных отклонений область установившихся значений коэффициентов задается неравенством
 ,
,
 ,
,  .
.
Структурная схема замкнутой системы приведена на рис. 2.2. Система состоит из четырех основных блоков: объект управления (ОУ), модель (М), адаптивный регулятор (АР), адаптор (А). Для формирования коэффициентов регулятора и управляющего воздействия используется первая производная выходной переменной. Как правило, производная выходного сигнала не может быть измерена, поэтому требуется включение в систему либо наблюдателя, либо фильтра оценки про-изводных. Порядок фильтра может быть равен или быть на единицу

| |

| |
меньше порядка объекта. Постоянная времени фильтра выбирается на один или два порядка меньше, чем минимальная постоянная времени эталонной модели. Структурная схема системы с нестационарным объектом и фильтром оценки производных второго порядка изображена на рис. 2.3. Моделирование адаптивной системы рекомендуется выполнять в среде Matlab, приложение Simulink.
Порядок работы
3.1. Определить элементы матриц 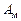 ,
, 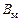 ,
, 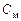 по заданным требованиям к качеству процессов, статическая ошибка работы системы допускается равной 5 % (см. табл. 1.1).
по заданным требованиям к качеству процессов, статическая ошибка работы системы допускается равной 5 % (см. табл. 1.1).
3.2. Вычислить элементы матриц H как решение уравнения Ляпунова (2.19) при  .
.
Записать уравнения алгоритмов адаптации (2.20)–(2.22) с вычисленными значениями коэффициентов.
3.3. Собрать схему адаптивной системы (рис. 2.2), объект управления моделировать по схеме, приведенной на рис. 1.1.
3.4. Получить графики переходной характеристики системы (y (t)),управляющего воздействия (u (t))и процессов на выходе адаптора (  ) при r (t)=1(t), нулевых начальных условиях на интегрирующих элементах, g = g1 = 1. Определить показатели качества (s %,
) при r (t)=1(t), нулевых начальных условиях на интегрирующих элементах, g = g1 = 1. Определить показатели качества (s %, 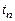 ,
,  – время сходимости процессов в адапторе).
– время сходимости процессов в адапторе).
3.5. Изменить значения коэффициентов (  = 1,
= 1, 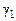 = 10 и
= 10 и  = 10,
= 10,
 1 = 10), сравнить переходные характеристики и процессы в адапторе
1 = 10), сравнить переходные характеристики и процессы в адапторе
с результатами п. 3.4 по показателям качества.
3.6. Изменить начальные условия в объекте (  ,
,  ), получить вид y(t), u(t),
), получить вид y(t), u(t),  ,
,  ,
, 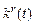 . Моделирование провести при g =
. Моделирование провести при g = 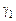 = 1, g = 1,
= 1, g = 1, 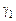 = 10. Сравнить с результатами п. 3.4.
= 10. Сравнить с результатами п. 3.4.
3.7. Изменить последовательно параметры объекта в 2 раза, выполнить п. 3.4, с помощью коэффициентов передачи адаптора добиться желаемого качества процессов.
3.8. Изменить модель объекта управления:  ,
,  (рис. 1.2). Провести моделирование при нулевых начальных условиях и различных значениях
(рис. 1.2). Провести моделирование при нулевых начальных условиях и различных значениях 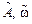 : а)
: а) 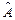 = 1,
= 1,  = 1,
= 1,
б) 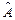 = 1,
= 1,  = 10, в)
= 10, в) 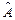 = 10,
= 10,  = 1. Для улучшения процессов в си-стеме изменить значения
= 1. Для улучшения процессов в си-стеме изменить значения 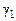 , g. Сравнить с результатами п. 3.4.
, g. Сравнить с результатами п. 3.4.
3.9*. Построить зависимость umaxот a, umax = max|u(t)| (при  ),
),  , где tk – время наблюдения за процессами в системе. Амплитуду параметрических возмущений выбирать из диапазона (0.1…100), например, (0.1, 1, 10, 50, 100),
, где tk – время наблюдения за процессами в системе. Амплитуду параметрических возмущений выбирать из диапазона (0.1…100), например, (0.1, 1, 10, 50, 100),  . Если с увеличением
. Если с увеличением 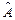 система становится неустойчивой, то следует подбором значений γ вернуть систему в устойчивое состояние.
система становится неустойчивой, то следует подбором значений γ вернуть систему в устойчивое состояние.
3.10. Рассчитать параметры фильтра оценки производных второ-
го порядка. Собрать схему системы с фильтром (рис. 2.3). Повторить пп. 3.5, 3.8.
Содержание отчета
1. Цель работы.
2. Исходные данные.
3. Структурная схема адаптивной системы.
4. Расчет параметров (пп. 3.1, 3.2, 3.11). Уравнения адаптивной системы и фильтра с вычисленными значениями параметров.
5. Графики процессов пп. 3.3, 3.5–3.11, график зависимости umax от a.
6. Выводы по работе.
––––––––––––––––––––––––––
* Пункты, отмеченные (*), выполняются по рекомендации преподавателя.
5. Контрольные вопросы
1. Виды и источники неопределённостей.
2. Виды возмущений.
3. Целевые критерии.
4. Агоритм скоростного градиента, формы алгоритма.
5. Вывод пропорционально-интегрального алгоритма адаптации для системы с объектом второго порядка и целевым функционалом (2.6).
6. Влияние начальных условий в адапторе на свойства системы.
7. Влияние начальных условий в объекте на свойства системы.
8. Влияние темпа параметрических возмущений на свойства системы.
9. Структурная схема адаптивной системы, функции основных блоков системы.
10. Расчет параметров фильтра оценки производных.
Лабораторная работа № 5
