ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ. 1. Произвести, если это необходимо, выравнивание прибора
1. Произвести, если это необходимо, выравнивание прибора.
2. Подключить сетевой шнур измерителя в питающую сеть.
3. Нажать кнопку "СЕТЬ", проверить, все ли индикаторы высвечивают цифру 0, а также, светится ли лампочка фотоэлектрического датчика.
Если выполняется упрощенный вариант (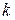 
задано), переходите к пункту 14.
4. Максимально приблизить грузы к оси, измерить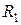 
.
5. Рукой отклонить стержень на любой угол и отпустить, предоставив ему возможность совершать свободные колебания.
6. Последовательным нажатием на кнопки "СБРОС" и "ПУСК" включить счетчики.
7. Измерить время 10 колебаний, для чего после появления на счетчике периодов цифры 9 нажать кнопку "СТОП".
8. Записать в таблицу результат.
9. Повторить измерения 3 раза.
10. Вычислить средний период колебаний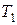 
по формуле
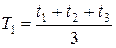
11. Максимально удалить грузы от оси вращения, измерить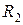 
.
12. Произвести аналогичные измерения периода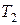 
(пп.5 –10).
13. По формуле (7) вычислить крутильную жесткость .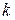
14. Установить маятник в таком положении, чтобы черта на ловушке
совпала с нулевой отметкой угловой шкалы.
15. Зарядить стреляющее устройство и произвести выстрел.
16. Измерить максимальный угол отклонения маятника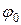 
.
17. Нажать кнопки "СБРОС" и "ПУСК", измерить время 10 колебаний.
18. Остановить маятник и измерить расстояние от оси вращения до
точки попадания снаряда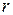 
.
19. По формуле (12) вычислить скорость снаряда (массы снаряда и грузов указаны на установке).
20. Повторить измерения 5 раз, изменяя расстояние до грузов.
21. Найти среднее значение скорости снаряда.
22. Вычислить среднюю абсолютную и относительную погрешности.
23. Результат измерений представить в виде
; 
%.
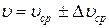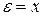24.Вывод.
25.ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ. Вычислить кинетическую энергию снаряда в момент столкновения с мишенью.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Скорость материальной точки.
2. Момент импульса материальной точки.
3. Закон сохранения момента импульса.
4. Угловая скорость.
5. Момент инерции твердого тела.
6. Теорема Штейнера.
ЛАБОРАТОРНАЯ РАБОТА 4
УНИВЕРСАЛЬНЫЙ МАЯТНИК (ФИЗИЧЕСКИЙ И МАТЕМАТИЧЕСКИЙ)
ЦЕЛЬ: изучение свободных колебаний физического и математического
маятников.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: лабораторная установка.
ОБЩИЕ УКАЗАНИЯ
Физический маятник представляет собой твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси 0 подвеса, не проходящей через центр масс С тела. Если маятник отклонен из положения равновесия на некоторый угол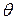 
, то в соответствии с уравнением динамики вращательного движения твердого тела момент М возвращающей силы 
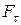можно записать в виде
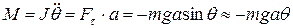, (1)
где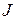 
– момент инерции маятника относительно оси, проходящей точку 0, а –расстояние между точкой подвеса и центром масс маятника С, 
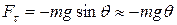– возвращающая сила, 
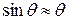соответствует малым колебаниям маятника (рис.1).
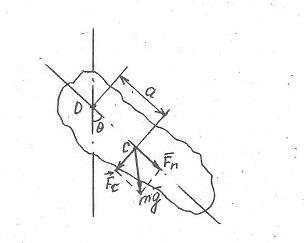
Рис. 1. Физический маятник.
Уравнение (1) можно представить в виде
.
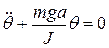Принимая
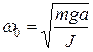, (2)
получим уравнение
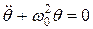, (3)
которое является уравнением свободных гармонических колебаний.
Решение уравнения (3) имеет вид
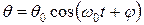, (4)
где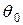 
– амплитуда колебаний; 
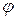– начальная фаза; 
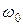– частота колебаний.
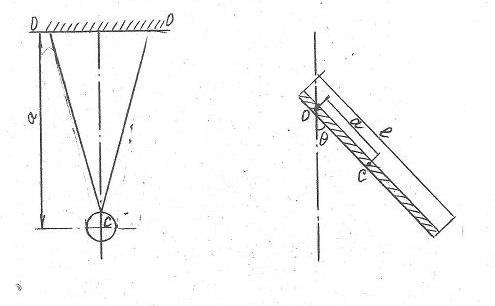
| Рис. 2. Математический маятник. | Рис. 3. Физический маятник в виде стержня. |
Период малых колебаний физического маятника
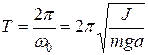. (5)
Математический маятник – это идеализированная система, состоящая из материальной точки массой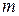 
, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести.
Момент инерции математический маятник
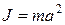. (6)
Математический маятник – можно представить как частный случай физического маятника, предположив, что вся масса физического маятника сосредоточена в центре масс С. Подставив (6) в (5), получаем формулу для периода малых колебаний математического маятника
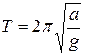. (7)
Из выражения (7) для вычисления ускорения свободного падения получаем формулу
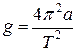. (8)
ОПИСАНИЕ УСТАНОВКИ
Исследуемый в лабораторной установке математический маятник схематически изображен на рис. 2. Он представляет собой стальной шарик радиуса 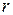на тонкой нити, пропущенной через центр шарика, концы нити закреплены на стойке.
Пренебрегая моментом инерции нити, запишем момент инерции маятника относительно оси 00 в виде
.
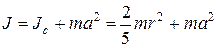Это соотношение следует из теоремы Штейнера, если учесть, что момент инерции однородного шара радиусом 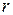и массой 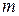относительно оси, проходящей через его центр
.
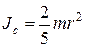Рассмотрим случай, когда радиус шарика мал по сравнению с длиной подвеса: <<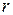 
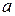. Тогда можно пренебречь слагаемым 
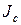по сравнению с 
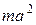и положить 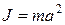, то есть мы получаем выражение, совпадающее с формулой (6). В данной работе проводится экспериментальная проверка соотношения (5) для физического маятника, имеющего формулу стержня. По стержню может перемещаться легкая опорная призма. Стержень колеблется относительно горизонтальной оси, опираясь нижним ребром призмы на закрепленную на штативе опорную площадку. Фиксируя призму в различных точках стержня, можно менять расстояние от оси качения маятника до его центра масс.
Момент инерции 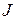стержня длиной 
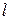и массой 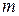относительно оси 0 (рис. 3) может быть найден с помощью теоремы Штейнера
.
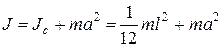Здесь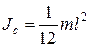 
– момент инерции однородного тонкого стержня относительно оси, проходящей через его центр масс С. Период колебаний стержня
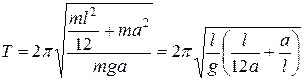. (9)
Вводя обозначения
, 
,
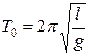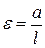формулу (9) можно представить в виде
,
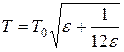или
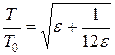(10)
ЛАБОРАТОРНОЕ ЗАДАНИЕ
Исследовать колебания стального шарика на подвесе (математического маятника) и рассчитать величину ускорения свободного падения. Изучить зависимость периода колебаний Т тонкого однородного стального стержня (физического маятника) от расстояния начала подвеса до центра масс.