Образец решения примера
Методические рекомендации
По выполнению практических работ
по дисциплине
ЕН.02 Элементы математической логики
по специальности СПО
Программирование в компьютерных системах
г. Благовещенск, 2014г.
Разработчик:
ГБПОУ БМПК преподаватель Алпатикова Н.Г.
Рассмотрено на заседании ПЦК информационно-математических дисциплин, специальности 230115 и профессии 180103.01
Председатель ПЦК __________/Шабаева Е.В.
Содержание
| Пояснительная записка | |
| Контрольные вопросы | |
| Практическая работа № 1 «Построение таблиц истинности» | |
| Практическая работа № 2 «Упрощение формул логики с помощью равносильных преобразований» | |
| Практическая работа № 3 «Представление булевой функции в виде совершенной ДНФ. совершенной КНФ, минимальной ДНФ» | |
| Практическая работа № 4 «Классификация булевых функций; проверка множества булевых функций на полноту» | |
| Практическая работа № 5 «Операции над множествами» | |
| Практическая работа № 6 «Решениезадач на выполнение теоретико-множественных операций и на подсчет количества элементов с использованием формулы количества элементов в объединении нескольких конечных множеств» | |
| Практическая работа № 7 «Определение логического значения длявысказываний, построение отрицаний к предикатам, формализация предложений с помощью логики предикатов» | |
| Практическая работа № 8 «Разбиение множества на классы» | |
| Информационное обеспечение |
Пояснительная записка
Математика является наукой, в которой все утверждения доказываются с помощью умозаключений, а именно путем использования законов человеческого мышления. Изучением таких законов занимается наука логика.
Логика – наука, изучающая методы доказательства и опровержений, то есть методы установления истинности или ложности одних высказываний (утверждений) на основе истинности или ложности других высказываний.
Математическая логика изучает схемы (формы) истинных высказываний, имеющих наибольшую степень общности, схемы математических доказательств и правила их вывода. Изучение исчисления высказываний как алгебраической системы составляет предмет алгебры логики, или булевойалгебры.
Математическая логика – современная форма логики, которая полностью опирается на формальные математические методы.
В соответствии с учебным планом колледжа на дисциплину "Элементы математической логики" отводится 68 аудиторных часов, в том числе 20 часов практических работ.
Решение задач по математической логике у студентов колледжа часто сопряжено с трудностями. Помочь студенту преодолевать эти трудности, научить применять теоретические знания к решению задач по всем разделам курса «Элементы математической логики» – основное назначение данного пособия.
Известно, что при самостоятельном решении задач многие студенты нуждаются в постоянных консультациях по приёмам и методам их решения, так как найти путь к решению задачи без помощи преподавателя или соответствующего пособия студенту не под силу. Такие консультации студент может получить в данном пособии.
В начале каждой практической работы приводятся основные определения и формулы, задачи с решением.
Ход практической работы:
1. Познакомиться с теоретическим материалом
2. Сделать краткий конспект теоретического материала в рабочих тетрадях (основные понятия, определения, формулы, примеры).
3. Ответить на контрольные вопросы.
4. В тетрадях для практических работ выполнить задания, которые указаны в работе.
5. Защита практической работы.
Критерии оценивания практических работ
За полностью выполненную практическую работу ставится «зачет». Если какие-либо задания не выполнены или выполнены неверно, то студент получает от преподавателя указания для выполнения этого задания.
Контрольные вопросы
| 1. Высказывание. Основные логические операции. |
| 2. Формулы логики. Таблица истинности. |
| 3. Конъюнктивные нормальные формы. |
| 4. Дизъюнктивные нормальные формы. |
| 5. Законы алгебры логики. |
| 6. Равносильные преобразования формул логики. |
| 7. Упрощение формул логики. |
| 8. Понятие булева вектора. N-мерный куб. |
| 9. Булева функция и способы её задания. |
| 10. Понятие совершенной ДНФ. |
| 11. Понятие совершенной КНФ. |
| 12. Операция двоичного сложения и её свойства. |
| 13. Многочлен Жегалкина. |
| 14. Выражение булевых функций через другие булевы функции. |
| 15. Полнота множества функций. |
| 16. Понятие замкнутого класса функций. |
| 17. Функция Шеффера |
| 18. Функция Пирса |
| 19. Понятие множества. Теоретико-множественные диаграммы. |
| 20. Операции над множествами и их свойства. |
| 21. Формула количества элементов в объединении множеств. |
| 22. Декартово произведение. |
| 23. Декартова степень множеств |
| 24. Теоретико-множественные операции и их связь с логическими операциями. |
| 25. Понятие предиката. Язык и алгебра предикатов. |
| 26. Кванторные операции над предикатами. |
| 27. Формализация предложений с помощью логики предикатов. |
| 28. Понятие бинарного отношения. Диаграмма бинарного отношения. |
| 29. Виды бинарных отношений. |
Практическая работа № 1 «Построение таблиц истинности»
Основные понятия и определения.
1.1. Высказывания и операции над ними
Математическая логика – это раздел математики, посвященный анализу методов рассуждений, при этом в первую очередь исследуются формы рассуждений, а не их содержание, т.е. исследуется формализация рассуждений? Это разновидность формальной логики, т.е. науки, которая изучает умозаключения с точки зрения их формального строения.
Основное неопределяемое понятие математической логики это высказывание. Под высказыванием понимают предложение, которое может принимать только два значения «истина» или «ложь». Обозначаются высказывания малыми латинскими буквами: a, b, ,…,х,…. или большими латинскими буквами A, B, C…
В математической логике не рассматривается смысл высказываний, определяется только их логическое значение – «истина» или «ложь». Известному немецкому математику и логику Эрнесту Шредеру пришло в голову предложить в качестве знака для обозначения ложного суждения цифру 0, что, конечно, привело к обозначению истины цифрой 1.
Исчисление высказываний – вступительный раздел математической логики, в котором рассматриваются логические операции над высказываниями.
Предикат – логическая функция от п переменных, которая принимает значения истинности или ложности.
Исчисление предикатов – раздел математической логики, объектом которого является дальнейшее изучение и обобщение исчисления высказываний.
Теория булевых алгебр (булевых функций) положена в основу точных методов анализа и синтеза в теории переключательных схем при проектировании компьютерных систем.
Примеры.
1. «Река Кола впадает в Кольский залив» – высказывание (истинное).
2. «Число32 кратно 3» – высказывание (ложное).
3. «Может быть, сегодня пойдет снег» – не высказывание.
4. «5х – 9 = 7» – не высказывание (неопределенное высказывание или высказывательная форма).
С помощью простых высказываний можно составлять более сложные, соединяя простые высказывания союзами «и», «или», связками «не», «следует» и др. Операции над высказываниями можно описывать при помощи некоторого математического аппарата.
Основные логические операции над высказываниями.
Отрицанием высказывания х называется высказывание, которое истинно тогда и только тогда, когда высказывание х ложно. Отрицание обозначается 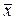 или Ø х (читается: «не х»).
или Ø х (читается: «не х»).
Логические операции можно задавать при помощи таблиц истинности, показывающих соответствие значений истинности высказываний. Для высказываний x и 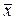 эта таблица имеет вид:
эта таблица имеет вид:
| х | 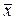 |
Конъюнкцией двух высказываний х и y называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания х и y. Конъюнкция обозначается: х Ù y,или х & y (читается: «х и y»). Таблица истинности для х Ù y имеет вид:
| х | y | х Ù y |
Дизъюнкцией двух высказываний х и y называется высказывание, ложное тогда и только тогда, когда оба высказывания х и y ложны. Дизъюнкция обозначается х Ú y (или x+y)(читается: «х или y»). Таблица истинности для х Ú y имеет вид:
| х | y | х Ú y |
Импликацией двух высказываний х и y называется высказывание, ложное тогда и только тогда, когда высказывание х истинно, а y – ложно. Импликация обозначается: х ® y (читается: «х влечет y» или «из х следует y»). Высказывание х называется посылкой импликации, а высказывание y – следствием. Таблица истинности для х ® y имеет вид:
| х | y | х ® y |
Эквиваленцией (эквивалентностью) двух высказываний х и y называется высказывание, истинное тогда и только тогда, когда истинности высказываний х и y совпадают. Эквиваленция обозначается: х « y, или х ~ y (читается: «х эквивалентно y» или «х тогда и только тогда, когда y»). Таблица истинности для х « y имеет вид:
| х | y | х « y |
1.2. Алгебра Буля.
Множество высказываний с введенными для них логическими операциями дизъюнкции, конъюнкции и отрицания основными законами этих действий называется алгеброй Буля. Алгебра Буля— исторически первый раздел математической логики, разработанный ирландским логиком и математиком Дж. Булем (George Boole (1815—1864) — английский математик и логик. Профессор математики Королевского колледжа Корка ). в середине XIX в. Буль применил алгебраические методы для решения логических задач и сформулировал на языке алгебры некоторые фундаментальные законы мышления
Законы алгебры Буля.
Коммутативные законы:
1. x Ù y º y Ù x;
2. x Ú y º y Ú x;
Ассоциативные законы:
1. x Ù (y Ù z) º (x Ù y) Ù z;
2. x Ú (y Ú z) º (x Ú y) Ú z;
Дистрибутивные законы:
1. x Ù (y Ú z) º (x Ù y) Ú (x Ù z);
2. x Ú (y Ù z) º (x Ú y) Ù (x Ú z);
Идемпотентные законы:
1. x Ù x º x;
2. x Ú x º x;
Законы логического сложения и умножения с 0 и 1:
1. x Ù 0 º 0;
2. x Ú 0 º x;
3. x Ù 1 º x;
4. x Ú 1 º 1;
Законы операции «черта»:
1. 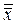 º x;
º x;
2. x Ú 0 º x;
3. x Ú 1 º 1;
4. 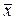 Ù x º 0;
Ù x º 0;
5. 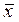 Ú x º 1;
Ú x º 1;
Законы Де Моргана ( Augustus de Morgan (1806- 1871) — шотландский математик и логик; профессор математики в Университетском колледже Лондона):
1. 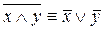 ;
;
2. 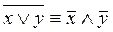 .
.
Сложением по модулю два (альтернативной дизъюнкцией, логи́ческим сложе́нием, исключа́ющим «ИЛИ», строгой дизъюнкцией) двух высказываний х и y называется высказывание, истинное тогда и только тогда, когда оба высказывания х и yпринимают разные значения. Дизъюнкция обозначается х Å y (читается: «или х, или y»). Таблица истинности для х Å y имеет вид:
| х | y | х Å y |
Стрелка Пирса – этоотрицание дизъюнкции.
Стрелка Пирса обозначается X ↓ Y. Читается «ни X, ни Y».
Введена в рассмотрение Чарльзом Пирсом (Сharles Peirce) в 1880—1881 г.г. Таблица истинности для стрелки Пирса имеет вид:
| х | y | х ¯ y |
Штрих Шеффера – это отрицание конъюнкции.
Введена в рассмотрение Генри Шеффером в 1913 г. (в отдельных источниках именуется как Пунктир Чулкова)
Штрих Шеффера обозначается x|y , задаётся следующей таблицей истинности:
| х | y | x|y |
1.3.Формулы алгебры логики
Формулами алгебры логики называются выражения, полученные из переменных x, y,… посредством применения логических операций: отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции, а также сами переменные, принимающие значения истинности высказываний x, y,….
Если в формулу алгебры логики вместо переменных x, y,… подставить конкретные высказывания, то получится высказывание, имеющее логическое значение «1» или «0».
Пример.
Высказывание x: «Волга впадает в Каспийское море» – истинное высказывание y: «Число 16 кратно 3» – ложное (y = 0), тогда формула А = x Ú y будет иметь логическое значение «1»: А = 1 (см. таблицу истинности для х Ú y).
На основе таблиц истинности основных логических операций можно составлять таблицы истинности для различных формул алгебры логики.
Две формулы алгебры логики называются равносильными или эквивалентными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы переменных (элементарных высказываний). Равносильность формул будем обозначать знаком «º».
Равносильность логических формул можно установить при помощи их таблиц истинности.
Пример. С помощью таблиц истинности проверить, являются ли равносильными формулы 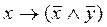 и
и 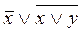 .
.
Решение. Составим таблицы истинности для каждой из формул А и В.
| x | y | 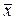 | 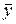 | 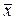 Ù Ù 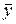 | 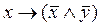 |
| x | y | 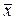 | x Ú y | 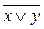 | 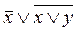 |
Ответ: данные формулы являются равносильными.
Другой способ доказательства равносильности логических формул – их упрощение с использованием равносильных преобразований.
2. Выражения одних логических операций через другие:
1) x ® y º 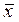 Ú y; 2)
Ú y; 2) 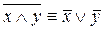 ;
;
3) x « y º (x ® y) Ù (y ® x); 4) 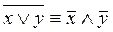 .
.
Для упрощения записи формул принят ряд соглашений. Скобки можно опускать, придерживаясь следующего порядка действий: Сначала выполняем действия в скобках, затем отрицание, затем выполняется конъюнкция. Если над формулой стоит знак отрицания, то скобки тоже опускаются.
Пример. Упростить логическую формулу: 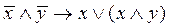 .
.
Решение. Используем основные равносильности.
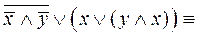
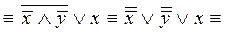
 .
.
Ответ: x Ú y.
Образец решения примера.
Являются ли эквивалентными следующие высказывания:
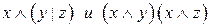
Решение.
Составим таблицы истинности для каждого высказывания.
| x | y | z | y|z | 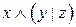 | 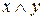 | 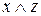 | 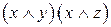 |
Значения x и y в пятом и восьмом столбцах не совпадают.
Вывод: данные высказывания не являются эквивалентными
Задания для практической работы:
Вариант 1
1.Укажите, в каких случаях высказывание истинно, а в каких ложно:
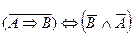
2.Являются ли эквивалентными следующие высказывания:
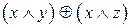 и
и 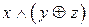
3.Решить булево уравнение:
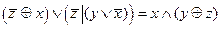
Вариант 2
1.Укажите, в каких случаях высказывание истинно, а в каких ложно:
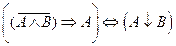
2.Являются ли эквивалентными следующие высказывания:
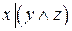 и
и 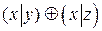
3.Решить булево уравнение:
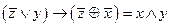
Вариант 3
1.Укажите, в каких случаях высказывание истинно, а в каких ложно:
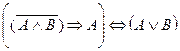
2.Являются ли эквивалентными следующие высказывания:
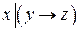 и
и 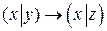
3.Решить булево уравнение:
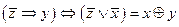
Вариант 4
1.Укажите, в каких случаях высказывание истинно, а в каких ложно:
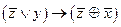
2.Являются ли эквивалентными следующие высказывания:
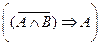 и
и 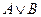
3.Решить булево уравнение:
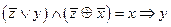
Вариант 5
1. Укажите, в каких случаях высказывание истинно, а в каких ложно:
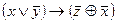
2.Являются ли эквивалентными следующие высказывания:
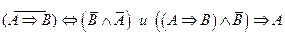
3.Решить булево уравнение:
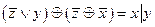
Вариант 6
1. Укажите, в каких случаях высказывание истинно, а в каких ложно:
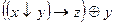
2.Являются ли эквивалентными следующие высказывания:
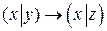
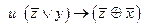
3.Решить булево уравнение:
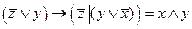
Вариант 7
1.Укажите, в каких случаях высказывание истинно, а в каких ложно:
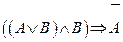
2.Являются ли эквивалентными следующие высказывания:
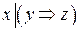 и
и 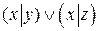
3.Решить булево уравнение:
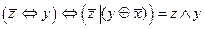
Вариант 8
1.Укажите, в каких случаях высказывание истинно, а в каких ложно:
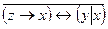
2.Являются ли эквивалентными следующие высказывания:
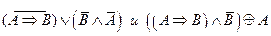
3.Решить булево уравнение:
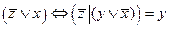
Вариант 9
1.Укажите, в каких случаях высказывание истинно, а в каких ложно:
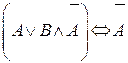
2.Являются ли эквивалентными следующие высказывания:
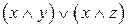 и
и 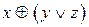
3.Решить булево уравнение:
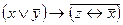 =1
=1
Вариант 10
1.Укажите, в каких случаях высказывание истинно, а в каких ложно:
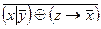
2.Являются ли эквивалентными следующие высказывания:
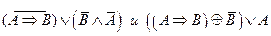
3.Решить булево уравнение:
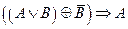 =0
=0
Вариант 11
1.Укажите, в каких случаях высказывание истинно, а в каких ложно:
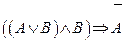
2.Являются ли эквивалентными следующие высказывания:
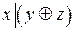 и
и 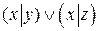
3.Решить булево уравнение:
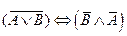 =0
=0
Вариант 12
1. Укажите, в каких случаях высказывание истинно, а в каких ложно:
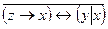
2.Являются ли эквивалентными следующие высказывания:
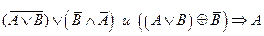
3.Решить булево уравнение:
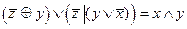
Вариант 13
1.Укажите, в каких случаях высказывание истинно, а в каких ложно:
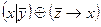
2.Являются ли эквивалентными следующие высказывания:
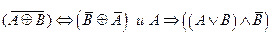
3.Решить булево уравнение:

Вариант 14
1.Укажите, в каких случаях высказывание истинно, а в каких ложно:
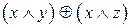
2.Являются ли эквивалентными следующие высказывания:
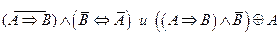
3.Решить булево уравнение:
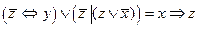
Вариант 15
1.Укажите, в каких случаях высказывание истинно, а в каких ложно:
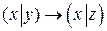
2.Являются ли эквивалентными следующие высказывания:

3.Решить булево уравнение:

