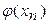Лабораторная работа №5
Решение нелинейных уравнений комбинированным методом хорд и касательных
Краткая теория
Будем рассматривать уравнения вида f(x)=0 (1). Пусть корень уравнения отделен и находится на отрезке [a,b]. Объединяя методы хорд и касательных, получим метод, дающий на каждом шаге сразу два приближения к корню- по недостатку и по избытку (рис.1).
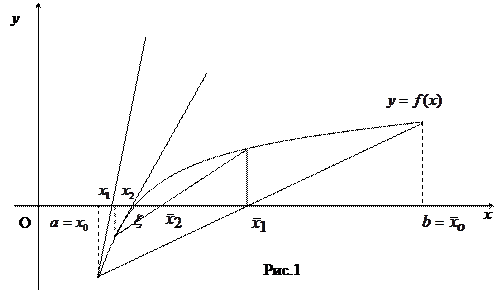
Здесь ξ – точный корень уравнения (1),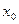 
и 
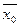- начальные приближения к корню по недостатку и по избытку соответственно, 
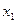и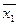 
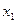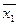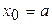
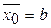
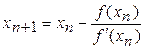
- точки пересечения касательной и хорды с осью Ох – первые приближения к корню. Далее комбинированный метод применяется на отрезке [ ; ]. В случае, изображенном на рис.1, удобно слева проводить касательную, а справа – хорду. Для вычисления новых приближений применяется формула, обозначим её 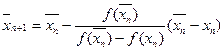(2):
(2)
В случае, если слева проводится хорда, а справа касательная, применяются формулы:
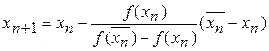(3)
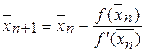
Правило выбора формул
Если знаки первой и второй производной функции f(x) на отрезке [a,b] совпадают, то применяются формулы (3), если разные - формулы (2).
Погрешность метода
Метод хорд и касательных обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1) , не превосходящую длины n-го отрезка:
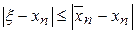
Алгоритм метода
1. Определить, какую пару формул ((2) или (3)) выбрать. Принять ,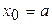 
.
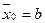2. Вычислить два новых приближения к корню 
и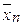 
по формуле (2) или (3).
3. Если длина отрезка [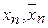 
] не превосходит заданной точности, то процесс заканчивается и в качестве точного корня можно взять или 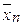, иначе идти к п.2.
Решение одного варианта
Отделить корни и уточнить их комбинированным методом с точностью до 0,001: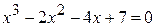 
.
Отделим корни аналитически. Находим
; 
.
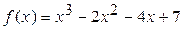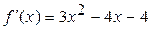D= 16+48=64.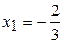 
, 
.
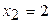Составим таблицу знаков функции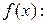 
| х |  |  |  | |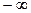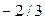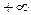
| знак f(x) | - | + | - | + |
Уравнение имеет три действительных корня: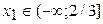 
; 
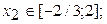
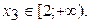
Уменьшим промежутки, содержащие корни, до единичной длины:
| х | -2 | -1 | ||||
| знак f(x) | - | + | + | + | - | + |
Следовательно,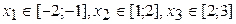 
.
Уточним корни комбинированным методом:
1. 
.
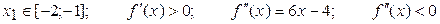Для вычислений применяем формулы
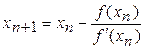
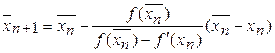(2)
Полагаем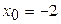 
, 
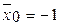
Все вычисления производим в таблице, обозначив
; 
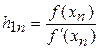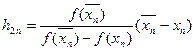
| n | |  |  |  |  |  | |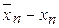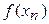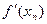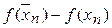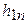
| |  |  | |||||
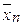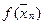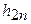| -2 | -1 | -0,0625 | |||||
| -1 | 0,08889 | ||||||
| -1,9375 | 0,0486 | -0,031 | 15,0117 | 0,7112 | -0,0021 | ||
| -1,8889 | 0,6802 | 0,0465 | |||||
| -1,9354 | 0,0005 | ||||||
| -1,9354 | 0,0005 |
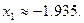
2. 
.
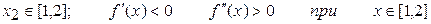Для вычисления применяем те же формулы , полагая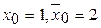 
.
Вычисления производим в таблице:
| n | | | | | | | |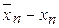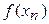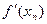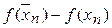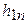
| | | | |||||
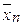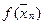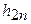| -5 | -3 | -0,4 | |||||
| -1 | 0,333 | ||||||
| -1,4 | 0,267 | 0,224 | -3,72 | -0,817 | -0,06 | ||
| -1,667 | -0,593 | 0,194 | |||||
| 1,46 | 0,013 | 0,009 | -3,4452 | -0,044 | -0,003 | ||
| 1,473 | -0,035 | 0,01 | |||||
| 1,463 | -0,001 | ||||||
| 1,463 | -0,001 |
.
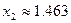3. 
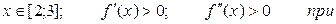
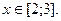
Для вычисления применяем формулы
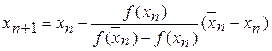
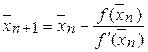, где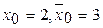 
Вычисления производим в таблице, обозначив
.
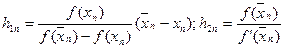| n | | | | | | | |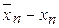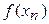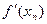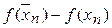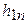
| | | | |||||
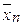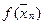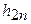| -1 | -0,2 | ||||||
| 0,364 | |||||||
| 2,2 | 0,436 | -0,832 | 6,301 | 1,707 | -0,212 | ||
| 2,636 | 0,875 | 0,139 | |||||
| 2,412 | 0,085 | -0,251 | 4,717 | 0,362 | -0,259 | ||
| 2,497 | 0,11 | 0,023 | |||||
| 2,471 | 0,003 | -0,008 | 4,466 | 0,013 | -0,002 | ||
| 2,474 | 0,005 | 0,001 | |||||
| 2,473 | 0,0007 | 4,455 | |||||
| 2,473 |
.
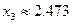Задание
Решить уравнение комбинированным методом с точностью до 0,001
1. 
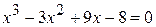
2. 
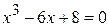
3. 
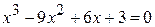
4. 
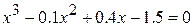
5. 
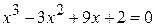
6. 
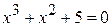
7. 
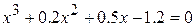
8. 
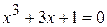
9. 
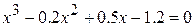
10. 
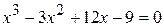
11. 
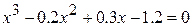
12. 
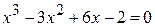
13.
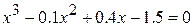
14. 
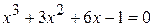
15. 
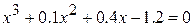
16. 
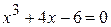
17. 
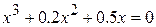
18. 
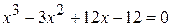
19. 
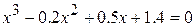
20. 
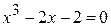
21.
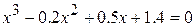
22. 
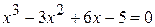
23. 
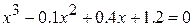
24. 
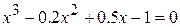
25. 
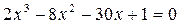
26. 
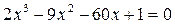
27. 
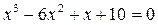
28. 
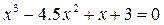
Лабораторная работа №6
Решение нелинейных уравнений методом итерации
Краткая теория
Будем рассматривать уравнения вида f(x)=0 (1). Пусть корень уравнения отделен и находится на отрезке [a,b]. Требуется найти этот корень с точностью ε. Для уточнения корня методом итерации приведем уравнение (1) к виду :
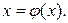(2)
Построим итерационную последовательность приближений к корню следующим образом:
выберем произвольно,
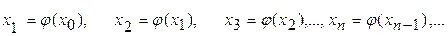(3)
Сходимость метода
Можно доказать, что если эта последовательность сходится, то она сходится к корню уравнения (2), а значит, и уравнения (1). Последовательность (3) сходится, если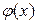 
является сжимающим отображением отрезка [a,b] в себя, что равносильно ограниченности модуля производной : 
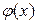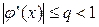для всех 
.
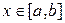Погрешность метода
Метод итерации обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1), не превосходящую длины n-го отрезка, умноженной на дробь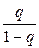 
: 
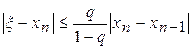, где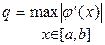 
.
Чтобы функция 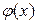обеспечивала сходимость последовательности (3), она должна иметь вид 
,
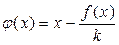где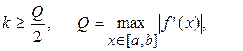 
знак k совпадает со знаком f’(x) на [a,b]. (4)
Алгоритм метода
1. Найти f’(x), ее знак и Q-наибольшее значение ее модуля на [a,b].
2. Выбрать число k, отвечающее условию (4).
3. Построить функцию 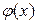, убедиться что 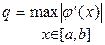<1.
4. Найти величину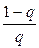 
ε.
5. Взять произвольно, например один из концов отрезка [a,b].
6. Вычислять значения 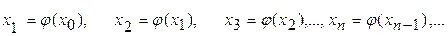до выполнения условия
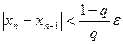
Решение одного варианта
Отделить корни, уточнить их методом итерации с точностью до 0,001:
.
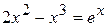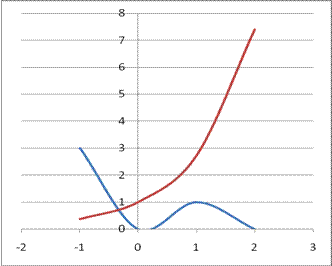
Отделим корни графически (см.рис.).
Уравнение имеет один действительный корень: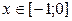 
Уточним корень методом итерации:
|
|
| |||||
| -1,0000 | -0,3420 | ||||||
| -0,3420 | -0,4511 | ||||||
| -0,4511 | -0,4856 | ||||||
| -0,4856 | -0,4929 | ||||||
| -0,4929 | -0,4942 | ||||||
| -0,4942 | -0,4944 | ||||||
| -0,4944 | -0,4945 |
1. 
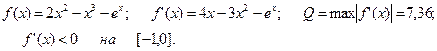
2. Выберем k=-4.
3. 
; 
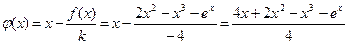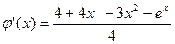; q=0,84<1
4. 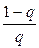, ε=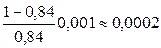 
.
5. За 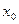примем левый конец отрезка -1.
6. Вычисления занесем в таблицу:
Поскольку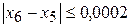 
, считаем, что корень уравнения 
.
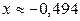Задание
Решить уравнение методом итерации с точностью до 0,001.
1. 
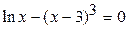
2. 
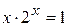
3. 
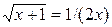
4. 
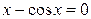
5. 
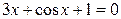
6. 
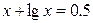
7. 
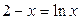
8. 
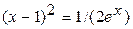
9. 
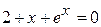
10. 
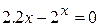
11. 
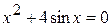
12. 
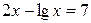
13. 
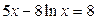
14. 
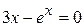
15. 
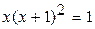
16. 
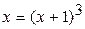
17. 
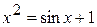
18. 
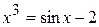
19. 
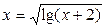
20. 
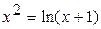
21. 
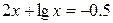
22. 
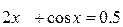
23. 
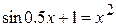
24. 
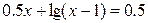
25. 10cosx-0,1x2=0
26. 
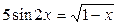
27. 
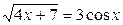
28. lg(x+5)=cosx