Пример выполнения лабораторной работы №1.2
Вычислить значение z и к , заданных формулами
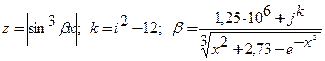
при исходных данных:
a) i=3; j=0,7; х=2;
b) i=4; j=0,8; х=4,5.
Так как в выражение для z входят β, в выражение для β входит k , то нужно вычислить последовательно k , β, z.
24 Таблица имен для переменных Блок-схема вычислений
| Переменная | Имя в программе |  Тип Тип |
| I | I | Целый |
| k | K | Целый |
| a | ALFA | Вещественный |
| β | BETA | Вещественный |
| x | X | Вещественный |
| z | Z | Вещественный |




|
|


|

 PROGRAM LAB1.2
PROGRAM LAB1.2
READ (5,*) I, ALFA, X
K= I**2-12
BETA=(1.25E6+ALFA**K)/((X**2+2.73)**(1./3.)
* -EXP(-X**2))
Z=ABS(SIN(BETA*X)**3)
WRITE(7, 1) K, Z
1 FORMAT (‘ K=’,I4,10X,’Z=’,E10.3)
END
Результат работы программы:
a) I=3 ALFA=0.7 X=2
K= -3 Z=0.997E+00
b) I=4 ALFA=0.8 X=4.5
K=4 Z=0.992E+00
Варианты заданий к л а б о р а т о р н о й работе №1.2в таблице 3.
Составить программу для вычисления значения переменных (графа 2), заданных формулами (графа 3) при исходных данных (графа 4). Номер варианта (графа 1). Таблица 3.
| Номер варианта | Вычисляемые переменные | Формулы для вычислений | Исходные данные | |||
| t, L |  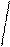 3 t – sin22x 3 t – sin22x 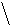  L= ; z = e – ty ; t = 2i - 1 z3/2 + 1 L= ; z = e – ty ; t = 2i - 1 z3/2 + 1 | a) i = 3; x = 2,7; y = 2*10-3 б) i = 5; x = 0,5 ; y = 0,01 | ||||
| p, r | P = | tg22rx | ; r = 2k+1 + 1;
α2 + 1 | а) k = 2; α = 3,7; y = 1,4 б) k = 3; α = 0,8; y = 1 | ||||
| λ, u | 125 * 106 sin2 x2  λ = ; λ = ;  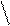 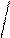 5 e4 - t-y y 5 e4 - t-y y  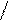  x = arcsin ; u = 2k + 1 x = arcsin ; u = 2k + 1 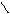 y2 + 1 y2 + 1 | а) k = 3; y = 34,7; t = 60 б) k = 1; y = 0,74; t = 2,5 | ||||
| γ, z | arcsin z – w * 0,75 γ  = ; = ;  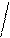 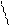 x2 3 0,34 * 10-5 e + x + sin t x2 3 0,34 * 10-5 e + x + sin t  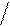  z = ; w = 2k + 1 z = ; w = 2k + 1 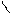 1 + x2 w 1 + x2 w | а) k = 2; x = 2,4; t = 1,52 б) k = 3; x = 5,12; t = 15,8 | ||||
| t, r | 1+tg y  t = ln |sin x2| + ; s = 3k – 2 k+1 t = ln |sin x2| + ; s = 3k – 2 k+1  (r + 1) y (r + 1) y  5 r = 0,284*105 e-s+2 + (y2+1)2 ; 5 r = 0,284*105 e-s+2 + (y2+1)2 ; | а) k = 5; x = 1,24; y = 3,24 б) k = 3; x = 2,38; y = 13,44 | ||||
| p, r |  3 cos2 λ u + 2r + 1 3 cos2 λ u + 2r + 1  p = ; 2,74 * 10-8 u λ p = ; 2,74 * 10-8 u λ  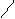 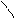 n t = esinr arcsin λ u ; r = 2n2 – n – 2 n t = esinr arcsin λ u ; r = 2n2 – n – 2 | а) n = 2 ; λ = 1,5; u = 0,2 б) n = 3; λ = 10; u = 28,4 | ||||
| k, n | k = | cos2 2yx | ; n = 2i+1 + 2 ;  n x = 1,84 * 10-8ey*y ey / (e2 + 1) n x = 1,84 * 10-8ey*y ey / (e2 + 1) | а) i = 1; y = 2 б) i = 2; y = 2,5 | ||||
| a, b | 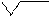 | u * b |3 + 5 b2+1 | u * b |3 + 5 b2+1  a = 1,84 * 10-5 b u a = 1,84 * 10-5 b u  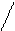  b = e sin s + ; s = 2n2 - 1 b = e sin s + ; s = 2n2 - 1  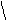 3 y + 1 3 y + 1 | а) n = 1; u = 14,2; y = 0,44 б) n = 2; u = 1,84; y = 12,3 | ||||
| k, n |  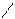 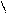 24,7 * 10-8 + x2 + λ y 24,7 * 10-8 + x2 + λ y  k = sin2 nx * | x2 + y2 – 3,44 * 102 | k = sin2 nx * | x2 + y2 – 3,44 * 102 |  3 n = 3i – 2; y = (1 – x2)2 3 n = 3i – 2; y = (1 – x2)2 | а) i = 1; λ = 14,2; x = 0,4 б) i = 2; λ = 8,2; x = 1,2 | ||||
| z, n | ky  z = arcsin ; z = arcsin ;  3 1 + y2 (k2 + 1) kx 3 1 + y2 (k2 + 1) kx  n = e-sin2y + ; k = 3i + 2 lnx-x2 n = e-sin2y + ; k = 3i + 2 lnx-x2 | а) i = 1; y = 11,2; x = 0,5 б) i = 2; y = 3,1; x = 1,2 | ||||
| c, d | c = |cos3(2dt)|; d = 3k-1 + 2;
4 αx
α2 + x2 | а) k = 2; α = 1,2; x = 5,2 б) k = 3; α = 1,8; x = 3,17 | ||||
| a, b |  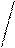 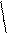 5 z – cos22x 5 z – cos22x  a = ; b = 2k2 – 1; λ = e-bx*x λ3/2 + 5,1 a = ; b = 2k2 – 1; λ = e-bx*x λ3/2 + 5,1 | а) k = 2; x = 13,8; z = 27,34 б) k = 1; x = 1,1; z = 7,8 | ||||
| u, v | arccos v – t * 34,2   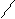  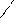 u = ; u = ; 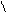 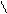 18,78 * 10-7 1+x2 + 3 x+sin t * v 18,78 * 10-7 1+x2 + 3 x+sin t * v  v = e-tx*x + ; t = 3i – 2i+1 tx v = e-tx*x + ; t = 3i – 2i+1 tx | а) i = 2; x = 3,41 б) i = 3; x = 14,1 | ||||
| x, t |  5 t2 + y2 + sin2 λ y t 5 t2 + y2 + sin2 λ y t  x = 3,4 * 10-6 yt x = 3,4 * 10-6 yt  λ 2 t = |sin y2| esin y ; λ = 3i+1 + 1 λ 2 t = |sin y2| esin y ; λ = 3i+1 + 1 | а) i = 1; y = 3,4 б) i = 2; y = 18,2 | ||||
| a, b | a = |tg3 2kb|; b = 2k – 1;  5 λz 5 λz  k = 2,34 * 10-6 e λz z2 + 1 k = 2,34 * 10-6 e λz z2 + 1 | а) n = 3; λ = 3,4; z = 1,3 б) n = 4; λ = 7,8; z = 9,8 | ||||
| p, r | 1 + sin y  p = + sin ln x; p = + sin ln x;  (2 + 1) y (2 + 1) y
r = 3 (y3+1)2 -0,185 * 10-5 es ; s = 4k – 3k+1 | а) k = 2; x = 0,34; y = 17,2 б) k = 3; x = 1,2; y = 24,3 | ||||
| m, α | m = |tg22αx|; α = 3k-1 + 1;  α y α y  x = e-y ; y2 + α x = e-y ; y2 + α | а) k = 2; y = 2,34 б) k = 3; y = 4,24 | ||||
| r, t | r = |sin32λt |; t = 2k-1 + 1;  3 zt 3 zt  λ = ezt; z2 + y4 λ = ezt; z2 + y4 | а) k = 2; z = 0,74; y = 5,3 б) k = 3; z = 1,34; y = 7,7 | ||||
| x, y |  5 sin32z 5 sin32z  x = ; y = 3i + 1; α = e-yz α3/2 + z x = ; y = 3i + 1; α = e-yz α3/2 + z | а) i = 1; z = 0,75 б) i = 2; z = 13,4 | ||||
Метки операторов
Обычно операторы программы выполняются последовательно друг за другом, т.е. после выполнения первого оператора выполняется второй, следующий за первым, после выполнения второго – выполняется третий и т.д. Такой порядок выполнения операторов называется естественным. Во многих случаях возникает необходимость нарушения естественного порядка вычислений. В таком случае следует указать оператор, который следует выполнить, пропустив ряд операторов, или, наоборот, вернувшись ближе к началу программы. Чтобы такое действие стало возможным оператор необходимо пометить.
Метка – это номер строки с оператором. Она состоит не более чем из четырех цифр, расположенных в строго отведенных позициях любой строки: со 2-й по 5-ю включительно. Метки выбираются программистом произвольно. Операторы, имеющие метку, называются помеченными. Правила присвоения меток:
1. Оператору можно присвоить только одну метку.
2. Две метки, отличающиеся ведущими нулями, считаются одинаковыми. Например,
метки 01, 0001, 1 – одинаковы.
3. Два оператора в одном программном модуле не должны иметь одинаковые метки.
4. Не обязательно расположение меток в порядке возрастания их номеров. Пример:
A = 25.7
7 B = 11.2
15 C = A ** 2 + SQRT (A * B)
7 D = C * (A + B)
2 D1 = D ** 2 / (A * B * C)
Этот пример иллюстрирует ошибку присвоения меток: два оператора в одном программном модуле имеют одинаковые метки (07и7).
Форматный ввод
Когда данные для программы обеспечивает сам программист, лучше использовать ввод под управлением списка (см. оператор READ(5,*)). Но может оказаться, что данные поступают из другого источника, или данных очень много и их следует как-то упорядочить. В подобных случаях используется форматный ввод. Рассмотрим пример форматного ввода: READ (5,100) I, J, K, (L(М), М=1,4)
5 FОRМАТ (I2, 2I3, 2(I1, I2))
По этому оператору вводится семь целых чисел, из них три простые переменные и четыре переменных с индексами, т.е. четыре элемента массива. В операторе FОRМАТ указано количество позиций в строке исходных данных, отводимых под каждое число. На число Iотведено две позиции, на число L и К – по 3 позиции, на первый и третий элементы массива – по одной позиции, на второй и четвертый – по две позиции, Если строка записи исходных данных имеет вид: 12 33 45 67
то в результате выполнения оператора READ получим
I J К L(1) L(2) L(3) L(4)
I 2 34 5 6 0 7
Общая форма F спецификации имеет такой же вид, как и при выводе, а именно
rFwd,где:
w- определяет ширину поля вывода, г – повторитель спецификации, а d – количество десятичных цифр в дробной части числа. Если число в записи данных содержит десятичную точку, то F – спецификацию записывают в виде rFw.0
Рассмотрим пример форматного ввода:
RЕАD (5, 50) А, В, С, D
FОRМАТ (F10.0, F10.4, F10.2, F10.6)
Пусть запись данных содержит следующие символы:
1.0 3.4 7 12345 67
В результате выполнения этих операторов переменная А получит значение 1.0, а переменная В – значение 3.47, так как символы пробела внутри поля ввода игнорируются. Значениеd, равное 0 и 4 в спецификациях F10.0 и F10.4. игнорируется, так как в каждом из указанных полей ввода имеется десятичная точка. По спецификации F10.2 содержимое позиций 21-30 (12345 ) считывается в ячейку С как число 123.45; так как в этом поле ввода нет десятичной точки, то цифра 2 в спецификации F10.2 определяет, что два последние, отличные от пробела символы, должны восприниматься как цифры дробной части числа. И, наконец, по спецификации F10.6 содержимое позиций 31-40 (67 ) считывается в переменную D как число 0.000067. В этом поле ввода нет десятичной точки, поэтому цифра 6 в спецификации F10.6 определяет, что последние шесть символов поля, отличных от пробела, воспринимаются как цифры дробной части числа. В поле ввода только два символа отличные от пробела, поэтому они и стали самыми младшими цифрами дробной части числа, а остальные цифры полагаются равными 0.
РАЗДЕЛ II.Лабораторная работа № 2
Алгоритмы
Совокупности правил, позволяющие решить какую-либо задачу, называют алгоритмами. Таким образом, все мы живем в мире алгоритмов. Они экономят силы и время человека, так как однажды усвоенным алгоритмом он может пользоваться всю жизнь.
Разработка алгоритмов для решения задач на компьютере требует специальных навыков. Чтобы облегчить построение и проверку алгоритма, запись его должна быть понятной, наглядной, допускать возможность некоторых изменений алгоритма.
Алгоритмам присущ ряд свойств, которые и объясняют, почему исполнитель может получить решение какой–либо задачи без особого труда.
1. Дискретность. Алгоритм состоит из последовательности законченных действий - шагов. Переход к следующему шагу возможен лишь после завершения предыдущего. Это свойство алгоритма всегда состоять из отдельных завершенных шагов называется дискретностью.
2. Определенность.Чтобы исполнитель мог решать задачу по заданному алгоритму, необходимо, чтобы каждая команда алгоритма всегда однозначно понималась и точно исполнялась. Это значит, что любая команда, выполненная много раз или различными исполнителями при одних и тех же исходных данных всегда должна давать один и то же результат. Эти требования и составляют свойство определенности алгоритма. Чтобы исключить возможность неоднозначного понимания команд алго-ритма, для описания алгоритмов разработаны специальные языки, в которых каждое предложение имеет абсолютно точный смысл.
3. Массовость.С помощью алгоритма можно решать не одну конкурентную задачу, а множество однотипных задач. Эти требования можно выполнять, если, разрабатывая алгоритм, придерживаться так называемого структурного подхода – применять вспомогательные алгоритмы, описывать алгоритм с помощью трех основных структур: следования, ветвления, повторения. Эти структуры на рисунке. 2:
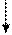



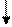












 |  |  | |||
следования

 ветвления
ветвления
повторения
Рис. 2

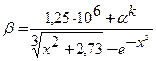

 3 αy
3 αy x = 2,34 * 10-5 eay
x = 2,34 * 10-5 eay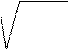
 t = 1,72*102 eαx
t = 1,72*102 eαx